2008级高三数学(文)模拟考试试题
一、选择题
1.设A、B、I均为非空集合,且满足![]() ,则下列各式中错误的是 ( )
,则下列各式中错误的是 ( )
|
C.![]() D.
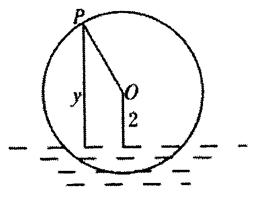
D.![]()
2.若条件![]() ,条件
,条件![]() 的 ( )
的 ( )
A.充分不必要条件 B.必要而不充分条件
C.充要条件 D.即不充分又不必要条件
3.将函数![]() 的图像按
的图像按![]() 平移后得到函数
平移后得到函数![]() 的图象,则向量
的图象,则向量![]() 可以是
可以是
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.奇函数![]() 的反函数是
的反函数是![]() 函数
函数![]() 在
在![]() 上是减函数,则
上是减函数,则
函数![]() 上是 ( )
上是 ( )
A.增函数 B.减函数 C.不是单调函数 D.常值函数
5.设![]() 都是非零实数,若(f)2004=-1那
都是非零实数,若(f)2004=-1那
么f(2005)= ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
6.若直线![]() 平移后与
平移后与![]() 相切,则
相切,则
实数m的值等于 ( )
A.3或13 B.3或-13 C.-3或13 D.-3或-13
7.![]() 展开式含
展开式含![]() 项的系数等于 ( )
项的系数等于 ( )
A.15 B.14 C.12 D.11
|
A.![]()
B.![]()
C.![]()
D.![]()
9.已知![]() 时,代数式
时,代数式![]() 的值是 ( )
的值是 ( )
A.正数 B.负数
C.0 D.介于-1至0之间的数
10.若对![]() 恒成立,则实数m的取值范围是
恒成立,则实数m的取值范围是
( )
A.(-2,3) B.(-3,3) C.(-2,2) D.(-3,4)
11.已知球面三个大圆所在平面两两垂直,则以三个大圆的交点为顶点的八面体的体积与球的体积之比是 ( )
A.2:![]() B.1:2
B.1:2![]() C.1;
C.1;![]() D.4:3
D.4:3![]()
12.债券市场发行三种债券,A种面值为1000元,一年到期本息和为1040年;B种面值为1000元,但买入价为960元一年到期本息和为1000元;C种面值1000元,半年到期本息和为1020元。设这三种债券的年收益率分别为a,b,c,则a,b,c的大小关系是
( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
二、填空题
13.设![]() 定义运算“*”:
定义运算“*”:![]() 则动点
则动点
![]() 的轨迹方程为
.
的轨迹方程为
.
14.![]() ,变量
,变量![]() 的取值范围是
.
的取值范围是
.
15.一同学在电脑中打出如下若干个圆(图中●表示实圆,○表示空心圆):●○●●○●●●○●●●●○●●●●●○……若将此若干个圆依此规律继续下去得到一系列圆,那么在前2007个圆中有 个空心圆.
16.某工程队有6项工程需先后单独完成,其中工程乙必须在工程甲完成后才能进行,工程丙必须在工程乙完成后才能进行,工程丁必须在工程丙完成后立即进行。安排这6项工程的不同排法种数是 .
三、解答题
17.已知向量![]()
(1)若![]() 的夹角;
的夹角;
(2)当![]() 时,求函数
时,求函数![]() 的最大值.
的最大值.
18.在“石室科技知识竞赛”中,比赛分三个环节:选答、抢答、风险选答。第一环节选答中,每位选后可以从6题(其中4道选择,2道操作题)中任选3题作答;第二环节抢答中,共为选手准备了5道抢答题,在每题的抢答中,每位选手抢到的概率相等;第三环节风险选答中,共为选手准备了A、B、C类题目,选手每答对一道A、B、C类题目,将分别得到300分,200分,100分,但若答错,则相应要扣去300分,200分,100分,选手答对一道A类、B类、C类题目的概率分别为0.6,0.7,0.8,现在甲、乙、丙三位选手比赛,试求:
(1)乙在第一环节中至少选到一道操作题的概率;
(2)在第二环节中,甲抢到的题目多于乙而不多于丙的概率;
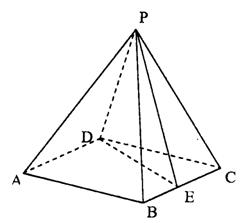
19.如图,四棱锥P—ABCD的底面是菱形,∠BCD=60°,PD⊥AD,点E是BC边的中点.
|
(2)若二面角P—AD—C的大小为60°,
AB=4,PD=![]()
①求点P到平面ABCD的距离
②求二面角P—AB—C的大小
20.已知定义在R上的函数![]() 的图像关于原点对称,当x=1时,
的图像关于原点对称,当x=1时,![]() 取极小值-2
取极小值-2
| |
(2)解关于x的“不等式![]() ”
”
21.数列![]() 满足
满足![]()
(1)求![]() ;
;
(2)是否存在一个实数t,使得![]() ,
,![]() 为等差数列,有,则求出t,并予以证明,没有,则说明理由;
为等差数列,有,则求出t,并予以证明,没有,则说明理由;
(3)求数列![]() 的前n项和Sn。
的前n项和Sn。
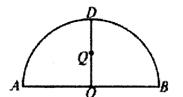
22.如图,ADB为半圆,AB为半圆直径,O为半圆圆心,且OD⊥AB,Q为线段OD的中点,已知AB=4,曲线C过Q点,运点P在曲线C上运动且保持PA+PB的值不变。
(1)建立适当的平面直角坐标系,求曲线C的方程;
(2)过D点的直线l与曲线C相交于不同的两个点M、N,且M在D、N之间![]() ,求
,求![]() 的取值范围;
的取值范围;
(3)过D的直线l与曲线C相交于不同的两点M、N,求△OMN面积的最大值.
|
参考答案
BABAC DDBBA CC
13.![]()
14.![]()
15.61
16.20
17.(1)![]()
![]() 4分
4分
(2)![]() 4分
4分
当![]() 4分
4分
18.(1)![]() 4分
4分
(2)甲乙丙三人抢到的题目数分别为:1,0,4; 2,0,3; 2,1,2
![]() 4分
4分
(3)设丙得分是随机变量![]()
![]()
![]()
![]()
故丙选B类题得分期望值最大。 4分
19.(1)略 4分
(2)①作PO垂直于DE,PO即所求,为4 4分
| |
平面PAB的法向量![]()
![]() 所求二面角为60° 4分
所求二面角为60° 4分
20.(1)f(0)=0,
![]()
![]()
![]() 上递增。 4分
上递增。 4分
(2)![]() 2分
2分
当m=0时,解集为![]()
当m>0时,解集为![]()
当m<0时,解集为![]() 6分
6分
21.解:(1)![]() 2分
2分
(2)![]() 为等差数列,必须
为等差数列,必须![]()
![]() 成等差,得
成等差,得![]() 成等差。
成等差。
下列此时bn对一切![]() 定成等差数列。
定成等差数列。
![]() ∴当t=
∴当t=![]() 时,
时,![]() 是公差为1的等差数列。 5分
是公差为1的等差数列。 5分
(3)![]()
∴![]()
由![]()
记![]()
错位相减,得![]() 5分
5分
22.解:(1)以AB、OD所在直线分别为x轴、y轴,O为原点,建立平面直角坐标系.
![]() 2分
2分
∴曲线C以原点为中心,A、B为焦点的椭圆,
设其长半轴为a,短半轴为b,半焦距为c,
则![]()
∴![]()
∴曲线C的方程为:![]() 2分
2分
(2)设直线l的方程为![]() ,代入曲线C的方程并整理,得
,代入曲线C的方程并整理,得
![]()
设![]() 则
则
|
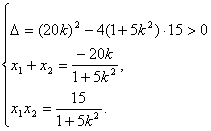
由①得![]()
又∵![]()
M在D、N之间,故![]()
∴![]()
由
而![]()
∴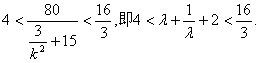
∴![]()
当l与y轴重合时,![]()
综上所述,![]() 4分
4分
(3)点O到直线MN的距离![]()
弦MN的长![]()
∴![]()
设![]()
∵![]()
∴![]()
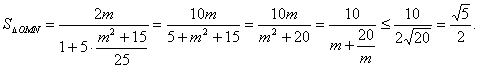
当且仅当![]() 时等号成立。此时
时等号成立。此时![]()
∴△OMN的面积有最大值为![]() 4分
4分