高三第二次调研测试数学试题
参考公式:
如果事件A、B互斥,那么 那么n次独立重复试验中恰好发生k
P(A+B)=P(A)+P(B)
次的概率![]()
如果事件A、B相互独立,那么 一组数据![]() 的方关
的方关
P(A·B)=P(A)·P(B) ![]()
如果事件A在一次试验中发生的概率是P, 其中![]() 为这组数据的平均数.
为这组数据的平均数.
第Ⅰ卷(选择题 共50分)
|
1.已知全集U=R,且A=![]() ,则A∩ 等于( )
,则A∩ 等于( )
A.![]() B.(2,3) C.
B.(2,3) C.![]() D.(-1,4)
D.(-1,4)
2.等差数列{an}的前n项和为Sn,若a7+a9=16,S7=7,则a12的值是 ( )
A.15 B.30 C.31 D.64
3.设m,n为直线,![]() 为平面,则
为平面,则![]() 的一个充分条件是 ( )
的一个充分条件是 ( )
A.m//n, n//α B.m⊥n,n⊥α,![]()
C.![]() D.m⊥
D.m⊥![]() ,
,![]() ⊥
⊥![]()
|
A.![]()
B.![]()
C.![]()
D.![]()
5.在![]() 的展开式中x4的系数是 ( )
的展开式中x4的系数是 ( )
A.-100 B.-80 C.80 D.100
6.已知变量![]() 满足约束条件
满足约束条件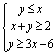 ,则目标函数
,则目标函数![]() 的最大值为
的最大值为
A.3 B.4 C.9 D.12
7.若A,B,C,D,E,F六个元素排成一列,要求A不排在两端,且B,C相邻,则不同的排法有 ( )
A.72种 B.96种 C.120种 D.144种
8.三棱锥![]() 的四个顶点都在半径为
的四个顶点都在半径为![]() 的球面上,底面
的球面上,底面![]() 所在的小圆面积为
所在的小圆面积为![]() ,则该三棱锥的高的最大值为 ( )
,则该三棱锥的高的最大值为 ( )
A.7 B.7.5 C.8 D.9
9.将直线![]() 绕着它与
绕着它与![]() 轴的交点按逆时针方向旋转
轴的交点按逆时针方向旋转![]() 角后,恰好与圆
角后,恰好与圆
![]() 相切,则
相切,则![]() 的一个值是 ( )
的一个值是 ( )
A.30° B.45° C.60° D.90°
|
A.2个 B.5个 C.6个 D.无数个
1.C 2.A 3.B 4.D 5.A 6.C 7.D 8.C 9.B 10.B
第Ⅱ卷(非选择题 共100分)
二、填空题:本大题人6小题,每小题5分,共30分。不需要写出解答过程,请把答案直接写在答题卡相应位置上。
11.为了考察甲、乙两种小麦的长势,分别从中抽取了6株苗,测得高如下(单位:cm):
| 甲 | 11 | 12 | 12 | 10 | 13 | 14 |
| 乙 | 12 | 13 | 9 | 13 | 12 | 13 |
由此可以估计, 甲 种小麦长得比较整齐。
12.在△ABC中,![]()
![]() ,
,![]() ,则
,则![]()
![]() 。
。
13.已知函数![]() 在区间
在区间![]() 内既有极大值,又有极小值,则实数
内既有极大值,又有极小值,则实数![]() 的取值范围是
的取值范围是
![]() 。
。
14.已知某人投蓝的命中率为![]() ,则此人投蓝4次,至少命中3次的概率是
,则此人投蓝4次,至少命中3次的概率是 ![]() 。
。
|
16.已知定义域为![]() 的函数
的函数![]() 对任意实数
对任意实数![]() 满足
满足![]() ,且
,且![]() ,给出下列结论:
,给出下列结论:
①![]() ;②
;②![]() 为奇函数;③
为奇函数;③![]() 是周期函数;④
是周期函数;④![]() 在
在![]() 内为单调函数
内为单调函数
其中正确的结论是 ②③ (填上所有正确结论的序号)
三、解答题:本大题5小题,共70分。请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤。
17.(本小题满分14分,第一小问满分6分,第二小问满分8分)
在△ABC中,![]() 的对边分别为
的对边分别为![]() 且
且![]() 成等差数列.
成等差数列.
(Ⅰ)求B的值;
(Ⅱ)求![]() 的范围。
的范围。
17.(Ⅰ)解法一:![]()
![]() 成等差数列,
成等差数列,
∴ ![]() …………………………………………2分
…………………………………………2分
由正弦定理得,![]()
代入得,![]()
即:sin(A+C)=2sinBcosB
∵A+B+C=π
∴sin(A+C)=sinB
∴![]() ……………………………………………………4分
……………………………………………………4分
又在![]() 中,
中,![]() ,
,![]()
![]()
![]()
![]() , ∴
, ∴![]() .……………………………………………………6分
.……………………………………………………6分
解法二:∵![]() 成等差数列,
成等差数列,
∴![]() …………………………………………2分
…………………………………………2分
由余弦定理,![]()
化简得, ![]() ……………………4分
……………………4分
∴![]()
∵ ![]() ……………………………………6分
……………………………………6分
(Ⅱ)解:![]()
![]() ,
,![]()
∴![]() …………………8分
…………………8分
![]()
![]() ……………………………………………………10分
……………………………………………………10分
![]()
![]() ,
,![]()
![]() ……………………………………………13分
……………………………………………13分
![]() 的范围是
的范围是![]() ……………………14分
……………………14分
|
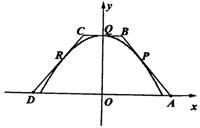
等腰梯形ABCD的三边AB,BC,CD分别与函数![]() ,
,![]() 的图象切于点P,Q,R。.求梯形ABCD面积的最小值。
的图象切于点P,Q,R。.求梯形ABCD面积的最小值。
|
18.解:设梯形![]() 的面积为
的面积为![]() ,点P的坐标为
,点P的坐标为![]() 。
。
由题意得,点![]() 的坐标为
的坐标为![]() ,直线
,直线![]() 的方程为
的方程为![]() 。
。
![]()
![]()
![]() ………………………………………………………………3分
………………………………………………………………3分
![]() 直线
直线![]() 的方程为
的方程为![]()
即:![]() ………………………………………………5分
………………………………………………5分
令![]() 得,
得,![]()
令![]() 得,
得,![]()
∴![]() ……………………………8分
……………………………8分
![]() ………………………10分
………………………10分
当且仅当![]() ,即
,即![]() 时,取“=”且
时,取“=”且![]() ,
,
∴当![]() 时,
时,![]() 有最小值为
有最小值为![]() .
.
∴梯形![]() 的面积的最小值为
的面积的最小值为![]() ……………………………………12分
……………………………………12分
19.(本小题满分16分,第一小问满分5分,第二小问满分5分,第二小问满分6分)
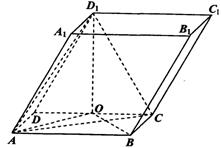
如图,在平行六面体ABCD—A1B1C1D1中,底面ABCD是矩形,AB=2,AD=1,顶点D1在底面ABCD上的射影O是CD的中点,侧棱与底面所成的角为60°。
|
(Ⅱ)求点O到平面AA1D1D的距离;
(Ⅲ)求二面角C—AD1—O的大小。
19.(Ⅰ)证明:![]()
![]() 在平面
在平面![]() 上的射影为O,
上的射影为O,
![]() ,
, ![]() ……………………2分
……………………2分
![]() 点
点![]() 为
为![]() 的中点,
的中点,![]() ,
,![]() OC=1
OC=1
又![]() ,
,![]() ,∠BOC=45°
,∠BOC=45°
同理∠AOD=45°, ∴∠AOB=90°。 ∴![]() ……………………4分
……………………4分
![]() ,
,![]() …………………………5分
…………………………5分
(Ⅱ)解法一:![]() ,
,![]()
又![]()
![]() ,
,![]() AD
AD![]() 平面
平面![]()
![]()
在平面![]() 内,作
内,作![]() ,垂足为
,垂足为![]() ,则
,则![]() 。
。
∴线段![]() 的长为点
的长为点![]() 到平面
到平面![]() 的距离……………………7分
的距离……………………7分
![]()
![]()
![]() 在平面
在平面![]() 上的射影为
上的射影为![]() 。
。
![]() 为侧棱
为侧棱![]() 与平面
与平面![]() 所成的角.
所成的角.
|
在![]() 中,
中,![]() =
=![]() 。
。
即点![]() 到平面
到平面![]() 的距离为
的距离为![]() ……10分
……10分
解法二:∵D1O⊥平面ABCD,∴DD1在平面ABCD上的射影为DO
∴∠D1DO为棱DD1与平面ABCD所成的角, ∴∠D1DO=60° …………7分
∵OD=1, ∴![]()
∴![]()
∵AD⊥DO,AD⊥D1O, ∴AD⊥平面D1DO ∴AD⊥DD1
设点O到平面ADD1A1的距离为h,
则![]() ………………9分
………………9分
∵![]()
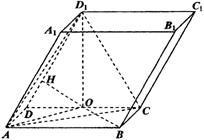
(Ⅲ)解:如图,作![]() 于
于![]() ,
,
作![]() 于
于![]() ,连结
,连结![]()
![]() ,
,![]()
又![]() ,
,![]()
又![]() ,
,![]()
![]() 为二面角
为二面角![]() 的平面角,……………………13分
的平面角,……………………13分
在![]() 中,
中,![]() ,
,![]() ,
,![]() .
.
在![]() 中,
中,![]() ,
,![]() ,
,![]()
取![]() 的中点
的中点![]() ,连结
,连结![]() ,则
,则![]() ,
,![]()
![]()
![]() ,
,![]()
在![]() 中,
中,![]()
![]() .
.
二面角![]() 的大小为
的大小为![]() .………………………………16分
.………………………………16分
20.(本小题满分14分,第一小问满分5分,第二小问满分9分)
已知![]() 为椭圆
为椭圆![]()
![]() 的右焦点,直线
的右焦点,直线![]() 过点
过点![]() 且与双曲线
且与双曲线![]() 的两条渐进线
的两条渐进线![]() 分别交于点
分别交于点![]() ,与椭圆交于点
,与椭圆交于点![]() .
.
(Ⅰ)若![]() ,双曲线的焦距为4。求椭圆方程。
,双曲线的焦距为4。求椭圆方程。
|
20.(Ⅰ)解:![]() ,
,![]() 是直线
是直线![]() 与双曲线两条渐近线的交点,
与双曲线两条渐近线的交点,
![]() ,
即
,
即![]() ………………2分
………………2分
![]() 双曲线的焦距为4,
双曲线的焦距为4,![]() ……………………4分
……………………4分
解得,![]()
![]() 椭圆方程为
椭圆方程为![]() …………5分
…………5分
(Ⅱ)解:设椭圆的焦距为![]() ,则点
,则点![]() 的坐标为
的坐标为![]()
![]() ,
, ![]()
![]() 直线
直线![]() 的斜率为
的斜率为![]() ,
,![]() 直线
直线![]() 的斜率为
的斜率为![]() ,
,
![]() 直线
直线![]() 的方程为
的方程为![]() …………………………………………7分
…………………………………………7分
由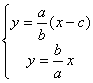 解得
解得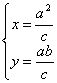 即点
即点![]()
设![]() 由
由![]() , 得
, 得![]()
即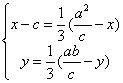
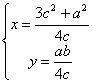
![]() ……10分。
……10分。
![]() 点
点![]() 在椭圆上,
在椭圆上,![]() ………………………………12分
………………………………12分
即 ![]() ,
,![]()
![]()
![]()
![]()
椭圆的离心率是![]() ……………………14分
……………………14分
21.(本小题满分14分,第一小问满分4分,第二小问满分10分)
设函数![]() 的图象是曲线C1,曲线C2与C1关于直线
的图象是曲线C1,曲线C2与C1关于直线![]() 对称。将曲线C2向右平移1个单位得到曲线C3,已知曲线C3是函数
对称。将曲线C2向右平移1个单位得到曲线C3,已知曲线C3是函数![]() 的图象。
的图象。
(Ⅰ)求函数![]() 的解析式;
的解析式;
(Ⅱ)设![]() 求数列
求数列![]() 的前
的前![]() 项和
项和![]() ,并求最小的正实数
,并求最小的正实数![]() ,使
,使![]() 对任意
对任意![]() 都成立。
都成立。
21.解:(I)由题意知,曲线C3向左平移我个单位得到曲线![]() ,
,
![]() 曲线
曲线![]() 是函数
是函数![]() 的图象 …………………………2分
的图象 …………………………2分
曲线![]() 与曲线
与曲线![]() 关于直线
关于直线![]() 对称,
对称,
![]() 曲线C1是函数
曲线C1是函数![]() 的反函数的图象
的反函数的图象
∵![]() 的反函数为
的反函数为![]()
![]() ………………………………………………………4分
………………………………………………………4分
(Ⅱ)由题设:![]() ,
,![]()
∴![]()
![]() ……6分
……6分
![]()
即 ![]()
![]() ①
①
∴![]() ②
②
由②—①得 ![]()
![]()
![]() ……………………8分
……………………8分
当![]()
![]()
![]()
当![]() 时,
时,![]()
![]() 当
当![]() 时,对一切
时,对一切![]() ,
,![]() 恒成立 ………………11分
恒成立 ………………11分
当![]() 时,
时, ![]()
![]()
记![]() ,则当
,则当![]() 大于比
大于比![]() 大的正整数时,
大的正整数时,
![]()
这就证明当![]() 时,存在正整数
时,存在正整数![]() ,使得
,使得![]() .
.
也就是说当![]() 时,
时, ![]() 不可能对一切
不可能对一切![]() 都成立.
都成立.
![]() 的最小值为
的最小值为![]() . …………………………14分
. …………………………14分