高三年级第八次月考数学试题(理)
本试题分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.共150分,考试时间120分钟.
第Ⅰ卷(选择题,共50分)
一、选择题:本大题共10小题,每小题5分,共50分.在每小题列出的四个选项中,只有一项是符合题目要求的.
1.![]() ( )
( )
A.![]() B.
B.![]() C.1 D.-1
C.1 D.-1
2.若角![]() 的终边落在直线
的终边落在直线![]() 上,则
上,则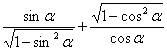 的值等于 ( )
的值等于 ( )
A.0 B.2 C.-2 D.![]()
3.若不等式![]() 的解集为
的解集为![]() ,则实数
,则实数![]() 等于 ( )
等于 ( )
A.8 B.2 C.-4 D.-8
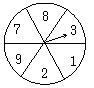
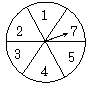 4.如图所示,在两个圆盘中,指针在本圆盘每个数所在
4.如图所示,在两个圆盘中,指针在本圆盘每个数所在
区域的机会均为![]() ,那么两个指针同时落在奇数所在
,那么两个指针同时落在奇数所在
区域的概率是 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
5.直线![]() 上的点到圆
上的点到圆![]() 上的点的最近距离是 ( )
上的点的最近距离是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.已知函数![]() ,则使
,则使![]() 为减函数的区间是 ( )
为减函数的区间是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.数列![]() 是各项均为正数的等比数列,
是各项均为正数的等比数列,![]() 是等差数列,且
是等差数列,且![]() ,则有 ( )
,则有 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]() 的大小不确定
的大小不确定
8.球面上有三点,其中任意两点间的球面距离等于大圆周长的![]() ,经过这三点的小圆周长
,经过这三点的小圆周长
为![]() ,则球的体积为 ( )
,则球的体积为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9.如图所示的阴影部分由方格纸上3个小方格组成,我
们称这样的图案为![]() 形(每次旋转
形(每次旋转![]() 仍为
仍为![]() 形图案),
形图案),
那么在由![]() 个小方格组成的方格纸上可以画出不同
个小方格组成的方格纸上可以画出不同
位置的![]() 形图案的个数是( )
形图案的个数是( )
A.16 B.32
C.48 D.64
10.在![]() 中,
中,![]() 是
是![]() 边上的高,若
边上的高,若![]() ,则实数
,则实数![]() 的值为
的值为
|
A.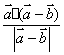 B.
B.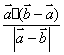 C.
C.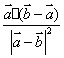 D.
D.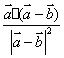
第Ⅱ卷(非选择题 共100分)
二、填空题:本大题共7小题,每小题4分,共28分.
11.命题:若![]() ,
,![]() 都是偶数,则
都是偶数,则![]() 是偶数,其逆否命题是__________________.
是偶数,其逆否命题是__________________.
12.![]() 的展开式中
的展开式中![]() 项的系数是
.
项的系数是
.
13.设![]() 为坐标原点,
为坐标原点,![]() 坐标满足
坐标满足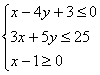 ,则
,则![]() 的最小值为________.
的最小值为________.
14.已知随机变量![]() 的分布列为
的分布列为![]() ,则
,则![]() =
.
=
.
15.过双曲线![]() 的左顶点
的左顶点![]() 作斜率为1的直线
作斜率为1的直线![]() ,若
,若![]() 与双曲线
与双曲线![]() 的两条渐近线分别相交于点
的两条渐近线分别相交于点![]() ,且
,且![]() ,则双曲线
,则双曲线![]() 的离心率是
.
的离心率是
.
16.设![]() ,若
,若![]() ,则
,则![]() .
.
17.![]() 和
和![]() 是两个腰长均为 1 的等腰直角三角形,当二面角
是两个腰长均为 1 的等腰直角三角形,当二面角![]() 为
为![]() 时,点
时,点![]() 和
和![]() 之间的距离等于 .(请写出所有可能的值)
之间的距离等于 .(请写出所有可能的值)
|
18.(本小题满分14分)
已知等比数列![]() 中,
中,![]() ,公比
,公比![]() 又分别是某等差数列的第7项,第3项,第1项.
又分别是某等差数列的第7项,第3项,第1项.
(Ⅰ)求![]() 的通项公式;
的通项公式;
(Ⅱ)设![]() ,
,![]() 为数列
为数列![]() 的前
的前![]() 项和,问:从第几项起
项和,问:从第几项起![]() ?
?
19.(本小题满分14分)
在![]() 中,角
中,角![]() 的对边分别为
的对边分别为![]() ,且满足
,且满足![]() .
.
(Ⅰ)求角![]() 的大小;
的大小;
(Ⅱ)已知函数![]() ,求
,求![]() 的最大值.
的最大值.
20.(本小题满分14分)
|
(Ⅰ)证明:![]() 平面
平面![]() ;
;
(Ⅱ)设![]() 分别为棱
分别为棱![]() 的中点,
的中点,
求直线![]() 与平面
与平面![]() 所成角的大小.
所成角的大小.
21.(本小题满分14分)
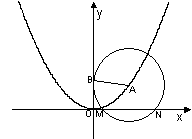
如图,已知圆![]() 过定点
过定点![]() ,圆心
,圆心![]() 在抛物线
在抛物线![]() 上运动,
上运动,![]() 为圆
为圆![]() 在
在![]() 轴上所截得的弦.
轴上所截得的弦.
(Ⅰ)证明:当![]() 点运动时,
点运动时,![]() 为定值.
为定值.
(Ⅱ)当![]() 是
是![]() 与
与![]() 的等差中项时,试判断抛物线
的等差中项时,试判断抛物线![]() 的准线与圆
的准线与圆![]() 的位置关系,并说明理由.
的位置关系,并说明理由.
22.(本小题满分16分)
已知函数![]()
(Ⅰ)求![]() 的值域;
的值域;
(Ⅱ)设m为方程![]() 的根,求证:当
的根,求证:当![]() 时,
时,![]() ;
;
(Ⅲ)若方程![]() 有4个不同的实根,求
有4个不同的实根,求![]() 的取值范围.
的取值范围.
参考答案
|
11)若![]() 不是偶数,则
不是偶数,则![]() ,
,![]() 不都是偶数. 12)840 13)1 14)6 15)
不都是偶数. 12)840 13)1 14)6 15)![]()
16)0或![]() 17)
17)![]()
18.解: (1)设公比为![]() ,由题意知,
,由题意知,![]() ,
,![]() ,
,
即![]() ,即
,即![]() ,
,![]() ,
,
![]() .
.![]() ,
,![]() .
.
(2) ![]() ,
,![]()
即![]() 时,
时, ![]() .
.![]() 从第14项起,
从第14项起, ![]() .
.
19.解: (1)由![]() 得
得![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() .
.
(2) ![]() ,
,
![]()
![]()
![]()
![]()
![]()
![]() 当
当![]() ,
,
即![]() 时,
时, ![]() .
.
20.(1)证明:设![]() 在底面的射影为
在底面的射影为![]() ,
,
![]()
![]() ,即
,即![]() 点在对角线
点在对角线![]() 上.
上.![]() ,
,
![]() ,
,![]() ,
,
![]() 点即为
点即为![]() 点,即
点,即![]() 平面
平面![]() .
.
(2)分别以![]() 为
为![]() 轴建立空间直角坐标系
轴建立空间直角坐标系![]() ,设边长为
,设边长为![]() ,
,
则![]() ,
,
而![]() ,
,
![]() ,设平面
,设平面![]() 的法向量为
的法向量为
![]() ,则
,则
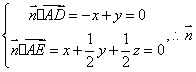 可取为
可取为![]() ,设
,设![]() 与平面
与平面![]() 所成角为
所成角为![]() ,
,
则![]()
![]() ,
,![]() 与平面
与平面![]() 所成角为
所成角为![]() .
.
21. 解: (1)设![]() ,则
,则![]() ,则圆
,则圆![]() 的半径
的半径![]() ,则圆
,则圆![]() 的方程为
的方程为
![]() ,令
,令![]() ,并将
,并将![]() 代入得
代入得![]() ,解得
,解得![]() ,
,![]() 为定值.
为定值.
(2)不妨设![]() ,由
,由![]()
![]()
![]() 知,
知,
![]() ,
,![]() 到抛物线准线
到抛物线准线![]() 的距离
的距离![]()
又圆![]() 的半径
的半径![]()
![]() =
=![]() ,
,
![]()
![]()
即圆![]() 与抛物线的准线总相交.
与抛物线的准线总相交.
22. 解:(1)![]() ,由
,由![]()
![]() 的值域为[-1,1]
的值域为[-1,1]
(2)∵m为方程f(x)=x的根,∴f(m)-m=0.
令![]()
∴F(x)为单调减函数,∴当x>m时,F(x)<F(m),即当x>m时,![]()
∴当x>m时,f(x)<x.
(3)令![]() ,
,
![]() ,
,
当![]()
![]() 单调递减;
单调递减;
在(0,1)和(1,+∞)单调增
∴当x∈(-1,1)时,![]()
x→-1-时,![]()
由h(x)为偶函数得,x→-1-时,h(x)→∞,x→1+,时,f(x)→-∞,
x→+∞时,h(x)→+∞
![]()
(若考虑到h(x)是偶函数,题意等价转化为h(x)在x![]() 上有2实根的问题,因而只需研究h(x)在
上有2实根的问题,因而只需研究h(x)在![]() 上单调性与h(0)的值以及h(x)在x→1+,x→1-,x→+∞的极限值,则可参照赋分,若仅从图象直观说明,则酌情扣分)
上单调性与h(0)的值以及h(x)在x→1+,x→1-,x→+∞的极限值,则可参照赋分,若仅从图象直观说明,则酌情扣分)
