高三年级第三次调研考试数学试题
本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,满分150分,考试时间120分钟。
第Ⅰ卷(选择题 共50分)
一、选择题:本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中恰有一项是符合题目要求的.
1.若集合![]() ,
,![]() ,那么
,那么![]() =
=
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.已知一组数据![]() 的平均数
的平均数![]() ,方差
,方差![]() ,则数据
,则数据![]() ,
,![]() ,
,![]() ,
,![]() 的平均数和标准差分别为
的平均数和标准差分别为
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.若命题甲:“p且q是真命题”,命题乙:“p或q是真命题”,则命题甲是命题乙的
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
4.若椭圆![]() 的离心率为
的离心率为![]() ,则双曲线
,则双曲线![]() 的离心率是
的离心率是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.已知函数![]() 的值域为
的值域为![]() ,设
,设![]() 的最大值
的最大值
为M,最小值为m,则![]() =
=
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.已知关于x方程![]() 无实根,其中
无实根,其中![]() ,则
,则![]() 可能取的一个
可能取的一个
值是
A.1 B.2 C.-2 D.-3
7.已知向量![]() ,
,![]() 若向量
若向量![]() 与
与![]() 的夹角为
的夹角为![]() ,则直线
,则直线
![]() 与圆
与圆![]() 的位置关系为
的位置关系为
A.相交且不过圆心 B.相交且过圆心
C.相切 D.相离
8.已知O,A,M,B为平面上四点,且![]() ,则
,则
A.点M在线段AB上 B.点B在线段AM上
C.点A在线段BM上 D.O、A、M、B四点一定共线
9.已知![]() ,定义
,定义![]() ,例如:
,例如:
![]() ,则函数
,则函数![]()
A.是偶函数不是奇函数 B.是奇函数不是偶函数
C.既是奇函数又是偶函数 D.既不是奇函数又不是偶函数
10.以一个长方体的四个顶点为顶点的四面体中,四个面都是直角三角形的四面体有
A.8个 B.16个 C.24个 D.48个
第Ⅱ卷(非选择题 共100分)
二、填空题:本大题共6小题,每小题5分,共30分.
11.在![]() 中,角A,B,C的对边分别为
中,角A,B,C的对边分别为![]() ,若
,若![]() ,则此三
,则此三
角形最大边长为 ▲ .
12.已知![]() 的展开式中,二项式系数之和为64,则它的二项展开式的中间项是
的展开式中,二项式系数之和为64,则它的二项展开式的中间项是
▲ .
13.已知x、y满足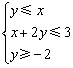 ,则
,则![]() 的最大值为 ▲ .
的最大值为 ▲ .
14.已知球O和球面上A、B、C三点,OA与截面ABC所成的角为![]() ,且
,且![]() 是边
是边
长为![]() 的等边三角形,则球O的表面积为 ▲ .
的等边三角形,则球O的表面积为 ▲ .
15.抛一枚均匀硬币,正、反面出现的概率都是![]() ,反复投掷,数列
,反复投掷,数列![]() 定义如下:
定义如下:
![]() ,若
,若![]() ,则事件“
,则事件“![]() ”
”
的概率为 ▲ .
16.已知函数![]() ,其中
,其中![]() 表示不超过x的最大整数,如:
表示不超过x的最大整数,如:![]() ,
,![]() ,
,
![]() ,若
,若![]() ,则
,则![]() 的值域为 ▲ .
的值域为 ▲ .
三、解答题:本大题共5小题,共70分,解答时应写出文字说明、证明过程或演算步骤.
17.(本小题满分12分)
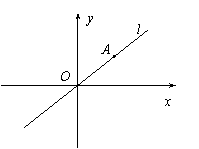 如图,已知A是直线
如图,已知A是直线![]() 上一点,
上一点,![]() .
.
(Ⅰ)若抛物线C的顶点在坐标原点,焦点在坐标轴
上且经过点A,求抛物线C的标准方程;
(Ⅱ)若直线l是双曲线![]() 的一
的一
条渐近线,且双曲线的右焦点在直线l上的射
影恰为点A,求双曲线的方程.
18.(本小题满分14分)
假设某地区2007年教育投入400万元,其中有240万元用于义务教育,预计在今后
的若干年内,该地区每年教育投入平均比上一年增长10%.另外,每年教育投入中,
义务教育的投入资金均比上一年增加60万元,那么,到哪一年底,
(Ⅰ)该地区历年义务教育投入的累计资金(以2007年为累计的第一年)将首次不
少于3600万元?
(Ⅱ)当年用于义务教育的资金占该年教育投入资金的比例首次大于80%?(参考数据:![]() )
)
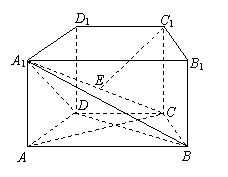 19.(本小题满分14分)
19.(本小题满分14分)
如图,在直四棱柱![]() 中,底面ABCD
中,底面ABCD
是等腰梯形,![]() ,侧棱
,侧棱
![]() .
.
(Ⅰ)证明:![]() 侧面
侧面![]() ;
;
(Ⅱ)设E是![]() 的中点,求异面直线
的中点,求异面直线![]() 与
与![]() 所成的角;
所成的角;
(Ⅲ)求二面角![]() 的大小.
的大小.
20.(本小题满分14分)
已知数列![]() 的前n项和
的前n项和![]() 满足:
满足:![]() (a为常数,且
(a为常数,且![]() ).
).
(Ⅰ)求![]() 的通项公式;
的通项公式;
(Ⅱ)设![]() ,若数列
,若数列![]() 为等比数列,求a的值;
为等比数列,求a的值;
(Ⅲ)在满足条件(Ⅱ)的情形下,设![]() ,数列
,数列![]() 的前n项和为
的前n项和为
Tn,求证:![]() .
.
21.(本小题满分16分)
设函数![]() ,其图象在点
,其图象在点![]() 处的切线
处的切线
的斜率分别为![]() .
.
(Ⅰ)求证:![]() ;
;
(Ⅱ)若函数![]() 的递增区间为
的递增区间为![]() ,求
,求![]() 的取值范围;
的取值范围;
(Ⅲ)若当![]() 时(k是与
时(k是与![]() 无关的常数),恒有
无关的常数),恒有![]() ,试求k的最小值.
,试求k的最小值.
高三年级第三次调研考试数学试题参考答案及评分标准
说明:
一、本解答给出了一种或几种解法供参考,如果考生的解答与本解答不同,可根据试题的主要考查内容参照评分标准制定相应的评分细则。
二、对解答题当考生的解答在某一步出现错误时,如果后续部分的解答未改变该题的内容和难度,可视影响的程度决定给分,但不得超过该部分正确解答应得分数的一半;如果后续部分的解答有较严重的错误,就不在给分。
三、解答右端所注的分数,表示考生正确做到这一步应得的累加分数。
四、只给整数分数,选择题和填空题不给中间分数。
一、选择题:每小题5分,满分50分.
1. C 2. B 3. A 4. B 5. C 6. A 7. D 8. B 9. B 10.C
二、填空题:每小题5分,满分30分.
11. ![]() 12.
12.
![]() 13.
13. ![]() 14.
14. ![]() 15.
15.![]() 16.
16. ![]()
三、解答题;
17.解:(Ⅰ)设A点坐标为![]()
![]() ,∴
,∴![]() ,
,
![]() ,∴
,∴![]() 点坐标为
点坐标为![]() ,……………………2分
,……………………2分
若抛物线开口向右,设抛物线标准方程为![]() ,
,
将点A坐标代入![]() 得
得![]() ,
,
此时抛物线标准方程为![]() ;……………………4分
;……………………4分
若抛物线开口向上,设抛物线标准方程为![]() ,
,
将点A坐标代入![]() 得
得![]() ,
,
此时抛物线标准方程为![]() ;
………………6分
;
………………6分
所以抛物线标准方程![]() 或
或![]() .
.
(Ⅱ)双曲线的右焦点为![]() ,一条渐近线为
,一条渐近线为![]() ,
,
因为双曲线的右焦点F在直线l上的射影为点A,
![]() , ∴
, ∴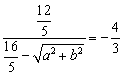 , 化简得
, 化简得![]() ,…① ……8分
,…① ……8分
又直线l是双曲线![]() 的一条渐近线,
的一条渐近线,
∴![]() , ………② ……………………10分
, ………② ……………………10分
由①②解得![]() , ……………………11分
, ……………………11分
故双曲线的方程为![]() . ……………………12分
. ……………………12分
18.解:(Ⅰ)设该地区义务教育的投入资金形成数列![]() ,
,
由题意可知![]() 是等差数列,其中
是等差数列,其中![]() ,
,
则![]() ,
……………4分
,
……………4分
令![]() ,即
,即![]() ,而n是正整数,
,而n是正整数,![]() .………6分
.………6分
(Ⅱ)设每年教育投入资金形成数列![]() ,由题意可知
,由题意可知![]() 是等比数列,
是等比数列,
其中![]() ,则
,则![]() ,
……………………10分
,
……………………10分
由题意可知![]() ,有
,有![]() , …………11分
, …………11分
满足上述不等式的最小正整数![]() .
.
到2011年底,当年用于义务教育的投入资金占该年教育投入资金的比例首次大于
80%. ………………14分
 19.(Ⅰ)证明:在等腰梯形ABCD中,
19.(Ⅰ)证明:在等腰梯形ABCD中,
由![]()
可知![]() ,
,![]() ,
,
![]() ,即
,即![]() ,
,
由![]() 是直棱柱,
是直棱柱,
知![]() 底面ABCD,即
底面ABCD,即![]() ,所以
,所以![]() 侧面
侧面![]() ;……………4分
;……………4分
(Ⅱ)连![]() ,由直棱柱的性质可知
,由直棱柱的性质可知![]() 是矩形,
是矩形,
又E是![]() 的中点,所以
的中点,所以![]() 三点共线,因为
三点共线,因为![]() ,
,
所以异面直线![]() 与
与![]() 所成的角就是
所成的角就是![]() 与AD所成的角,即
与AD所成的角,即![]() . ……6分
. ……6分
在![]() 中,
中,![]() ,
,
由余弦定理得![]() ,即异面直线
,即异面直线![]() 与
与![]() 所成的角为
所成的角为![]() ;…9分
;…9分
(Ⅲ)由![]() 得
得![]() 平面
平面![]() ,设O是底面梯形ABCD对角线的
,设O是底面梯形ABCD对角线的
交点,过点O作![]() 于H点,则
于H点,则![]() 平面
平面![]() ,过H点作
,过H点作![]() 为
为
垂足,连OF,则![]() ,所以
,所以![]() 为二面角
为二面角![]() 的平面角,…12分
的平面角,…12分
在直角![]() 中求得
中求得![]() ,在直角
,在直角![]() 中求得
中求得![]()
所以在直角![]() 中,
中,![]()
即所求二面角为![]() .
…………………………14分
.
…………………………14分
20.解:(Ⅰ)![]() ∴
∴![]()
当![]() 时,
时,![]()
![]() ,即
,即![]() 是等比数列. ∴
是等比数列. ∴![]() ;
………………4分
;
………………4分
(Ⅱ)由(Ⅰ)知,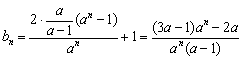 ,若
,若![]() 为等比数列,
为等比数列,
则有![]() 而
而![]()
故![]() ,解得
,解得![]() ,再将
,再将![]() 代入得
代入得![]() 成立,
成立,
所以![]() .
.
(III)证明:由(Ⅱ)知![]() ,所以
,所以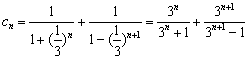
![]()
![]() ,
,
由![]() 得
得![]()
所以![]() ,
,
从而![]()
![]()
![]() .
.
即![]() .
…………………………14分
.
…………………………14分
21.解:(Ⅰ)![]() ,由题意及导数的几何意义得
,由题意及导数的几何意义得
![]() ,
,![]() (1)
(1)
![]() ,
(2)
………………2分
,
(2)
………………2分
又![]() ,可得
,可得![]() ,即
,即![]() ,故
,故![]() ………3分
………3分
由(1)得![]() ,代入
,代入![]() ,再由
,再由![]() ,得
,得
![]() ,
(3) ……………………4分
,
(3) ……………………4分
将![]() 代入(2)得
代入(2)得![]() ,即方程
,即方程![]() 有实根.
有实根.
故其判别式![]() 得
得
![]() ,或
,或![]() ,
(4)
……………………5分
,
(4)
……………………5分
由(3),(4)得![]() ;
……………………6分
;
……………………6分
(Ⅱ)由![]() 的判别式
的判别式![]() ,
,
知方程![]() 有两个不等实根,设为
有两个不等实根,设为![]() ,
,
又由![]() 知,
知,![]() 为方程(
为方程(![]() )的一个实根,则有根与系数的关系得
)的一个实根,则有根与系数的关系得
![]() ,
……………………9分
,
……………………9分
当![]() 或
或![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
故函数![]() 的递增区间为
的递增区间为![]() ,由题设知
,由题设知![]() ,
,
因此![]() ,由(Ⅰ)知
,由(Ⅰ)知![]() 得
得
![]() 的取值范围为
的取值范围为![]() ;
……………………12分
;
……………………12分
(Ⅲ)由![]() ,即
,即![]() ,即
,即![]() ,
,
因为![]() ,则
,则![]() ,整理得
,整理得![]() ,
,
设![]() ,可以看作是关于
,可以看作是关于![]() 的一次函数,
的一次函数,
由题意![]() 对于
对于![]() 恒成立,
恒成立,
故![]() 即
即![]() 得
得![]() 或
或![]() ,
,
由题意,![]() ,
,
故![]() ,因此
,因此![]() 的最小值为
的最小值为![]() .
……………………16分
.
……………………16分