高三年级第三次模拟考试数学试卷（文）
一、选择题（每题5分，共60分）
1．函数y=
的定义域为 （ ）
A．{xx≠
} B．（,+∞）
C．(－∞,) D．[,+∞]
2．复数z1=1+i,z2=x+2i(x∈R),若z1z2∈R,则x= （ ）
A．－2 B．－1 C．1 D．2
3．已知样本10,8，6,10,13,8,10,12,11,7，8,9，11,9，12,9，10,11,12,12,那么频率是0.3的范围
是 （ ）
A．5.5～7.5 B．7.5～9.5 C．9.5～11.5 D．11.5～13.5
4．下列函数中，在定义域内既为奇函数又为减函数的是 （ ）
A．y=sin2x B．y=
C．y=2x D．y=－2x3
5．函数y=cos2(2x+
)－sin2(2x+)的最小正周期是 （ ）
A．
B．2 C．4
D．
6．随着x的增大：①y=logax(a>1)的值增长的越来越慢 ②y=ax(a>1)的值增长速度越来越快，会表现为指数爆炸 ③y=kx+b(k>0)的值匀速增长 ④y=2x增长速度会超过并远远大于y=x2的增长速度，以上结论，正确的个数是 （ ）
A．1 B．2 C．3 D．4
7．由点P(2,4)向直线ax+y+b=0引垂线，垂足为Q(4,3),则a,b的值依次为 （ ）
A．－2,5 B．2，－11 C．
，－5 D．－，－11
8．先后抛掷三枚均匀的一角、伍角、壹元的硬币，则出现两枚正面，一枚反面的概率是（ ）
A．
B．
C．
D．
9．以下结论不正确的是 （ ）
A．根据2×2列联表中的数据计算得出k2≥6.635,而P(k2≥6.635)≈0.01,则有99%的把握
认为两个分类变量有关系
B．在线性回归分析中，相关系数为r，r越接近于1，相关程度越大；r越小，相关程度越小
C．在回归分析中，相关指数R2越大，说明残差平方和越小，回归效果越好
D．在回归直线
=0.5x－85中，变量x=200时，变量y的值一定是15
10．若a,b,c是Rt△的三边(c为斜边)长，则圆x2+y2=2被直线ax+by+c=0截得的弦长为（ ）
|
D．2
11．设
是两条不重合的直线，
、
是两个不重合的平面，给出下列四个命题：①若
，
，∥，∥，则∥ ②⊥，⊥，则∥ ③若⊥，⊥，则∥ ④若⊥，，则⊥，其中正确的命题个数为
（ ）
|
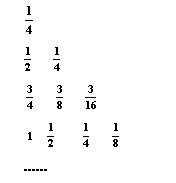
12．下表给出一个“直角三角形数阵”，记第i行，
第j列的数为aij,则a83= （ ）
A．
B．
|
D．1
二、填空题(每题4分，共16分)
13．正方体AC1中，AC1与A1D所成角等于____________.
14．向量
=(－2,3)，
=(1,m)，若、夹角为钝角，
则实数m的范围是_________.
15．右边程序运行结果输出S的值是_________.
16．已知实数x,y满足x2+y2≤1,x+y≤0,则z=x+2y
的最大值是___________.
三、解答题(共5个小题，满分64分，写出必要的过程及文字说明)
17．（本小题满分12分）
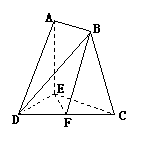已知
=(cos,sin),
=(cos,sin),0<
,
=
,求sin(－).
18．（本小题满分12分）
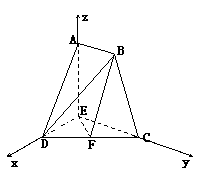
如图，在五面体ABCDE中，EA=ED=EC=2，且EA、ED、EC两两垂直，AB∥CE，AB=1，F为CD中点
（1）求证：BF∥平面ADE
（2）判断EF与面BCD能否垂直，证明你的结论.
19．（本小题满分12分）
已知椭圆C：x2+
,直线
：y=mx+1
（1）求证：当m∈R时，与C恒有两个不同交点；
（2）设交C于A、B两点，求AB中点M的轨迹.
|
20．（本小题满分14分）
设数列{an}的前n项和Sn=2n2，数列{bn}为等比数列，a1=b1且b2(a2－a1)=b1
（1）求{an},{bn}的通项公式；
（2）设cn=
，求数列{cn}的前n项和公式Tn.
21．(本小题满分14分)
已知f(x)=x3+bx在[－1,1]上是增函数
（1）求实数b的范围；
（2）若不等式b2－tb+1≥f(x)对任意x∈[－1,1]恒成立，求实数t的取值范围.
四、选考题（10分，请从所给的二道题中任选一道作答，并用2B铅笔在答题卡上把所选对应题目的题号涂黑）
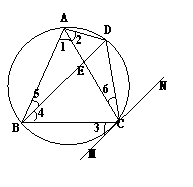
A．△ABC内接于⊙O，AB=AC，直线MN切⊙O于C，
弦BD∥MN，AC、BD交于点E
（1）求证：△ABE≌△ACD
（2）AB=6，BC=4，求AE
B．求点P(2，
)到直线
的距离.
参考答案
一、选择题：(每小题5分，共60分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | ||
| 答案 | B | A | B | D |
| D | A | A | D | B | B | C |
二、填空题(每小题4分，共16分)
13．90°
14. m<且m≠－
15.
12 16. 
三、解答题
17．（12分）
（3分）
sinsin+coscos=
（6分）
cos(－)=
（8分）
（10分）
∴sin(－)=－
（12分）
18．（12分）
（1）略 （6分）
（2）不垂直 （12分）
方法一：求出EF=
，BE=
，取EC中点G，BG=2，GF=1，BF=
∴△BEF是等腰三角形
∴EF与BF不垂直
∴EF与平面BDC不垂直.
方法二：向量法，如图建立坐标系
E(0,0，0)，F(1,1，0)，B(0,1，2)，C(0,2，0)
=(1,1，0)，
=(0,1，2)
∴EF与BC不垂直
∴EF与平面BDC不垂直.
19．（12分）
（1）方法一：直线亘这定点P(0,1) （2分）
而P(0,1)在椭圆C内 （3分）
∴与C恒有两个不同交点 （4分）
方法二：由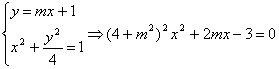
（2分）
△=(2m)2+4×3×(4+m2)>0 （3分）
∴与C恒有两个不同交点
（4分）
（2）方法一：设A(x1,y1),B(x2,y2),M(x,y)则
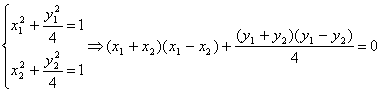（6分）
x1+x2+
=0(∵x1≠x2)
x1+x2=2x,y1+y2=2y,k=m （8分）
∴x+
m=0
（9分）
又y=mx+1 （10分）
消去m得4x2+(y－)2=
（12分）
∴M点轨迹方程为4x2+y2－y=0(y≠0)
方法二：由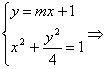
(4+m2)x2+2mx－3=0
（10分）
消去m得4x2+y2－y=0(y≠0)
∴M点轨迹方程为4x2+y2－y=0(y≠0) （12分）
20．（14分）
(理)（1）P1=，P2=
，P3=
（2）Pn+2－Pn+1=
∴
∴{Pn+2－Pn+1}是公比为－的等比数列
（10分）
（3） Pn+2－Pn+1=(P2－P1)·(－)n－1=(－)n+1
P2－P1=(－)2,P3－P2=(－)3,……，Pn－Pn－1=(－)n
相加：Pn－P1=(－)2+(－)3+…+(－)n=
[1－(－)n－1]
∴Pn=
（14分）
(文)（1）an=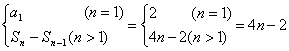
（4分）
b1=a1=2,b2=
,q=
bn=b1qn－1=2·()n－1
（7分）
（2）Cn=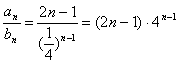
（8分）
Tn=1+3·41+5·42+……+(2n－1)·4n－1
4Tn=4+3·42+5·43+……+(2n－1)·4n
－3Tn=1+2·41+2·42+……+2·4n－1 －(2n－1)·4n
=－[(6n－5)4n+5]
∴Tn=
[(6n－5)4n+5]
21．（14分）
（理）（1）f′(x)=4+2ax－2x2，由题意f′(x)≥0在[－1,1]上恒成立 （2分）
∴
∴A=[－1,1]
（5分）
（2）方程f(x)=2x+x3可化为x(x2－ax－2)=0
∵x1≠x2≠0,
∴x1,x2是x2－ax－2=0两根 （7分）
△=a2+8>0,x1+x2=a,x1x2=2
∴x1－x2=
∵－1≤a≤1
∴x1－x2最大值是
（10分）
∴m2+tm+1≥3在t∈[－1,1]上恒成立
令g(t)=mt+t2－2
∴
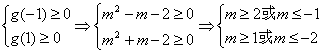
m≥2或m≤－2 （14分）
故存在m值，其取值范围为(－∞,－2)∪[2,+∞]
（文）（1）f′(x)=3x2+b
由已知f′(x)在[－1,1]上恒成立 （3分）
∴b≥－3x2在[－1,1] 上恒成立
∵－3x2在[－1,1]上最大值为0 （7分）
（2）f(x)在[－1,1]上最大值为f（1）=1+b （9分）
∴b2－tb+1≥1+b （10分）
即b2－(t+1)b≥0恒成立，由b≥0得
∴b－(t+1)≥0,t+1≤b恒成立
∴t≤－1 （14分）
四、选考题：（10分）
A．（1）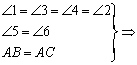
△ABE≌△ACD （5分）
（2）
△ABC∽△BEC
∴
（8分）
∴AE=
（10分）
B．P(2，
)
P(
) （3分）
x－
y+2=0
（7分）
D=
（10分）
C．设a=cos
,b=sin,c=cos,d=sin
（4分）
ac+bd=coscos+sinsin
（6分）
=cos(－)≤1
（10分）
方法二：只需证(ac+bd)2≤(a2+b2)(c2+d2) （6分）
即证：2abcd≤a2d2+b2c2 （8分）
即证：(ad－bc)2≥0
上式显然成立
∴原不等式成立. （10分）