高三年级第四次月考数学试题(理)
YC 2020
第Ⅰ卷(选择题 共60分)
一、选择题:本大题共10小题,每小题5分,共50分.在每小题列出的四个选项中,只有一项是符合题目要求的.
1.复数![]() 的虚部为
的虚部为 ![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.设函数![]() 在
在![]() 处连续,且
处连续,且![]() ,则
,则![]() 等于 ( )
等于 ( )
A.-1 B.1 C.0 D.-2
3.若![]() ,
,![]() ,则
,则![]() = ( )
= ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.等差数列![]() 中,
中,![]() ,则此数列的前20项和为 ( )
,则此数列的前20项和为 ( )
A.160 B.180 C.200 D.220
5.下列函数既是奇函数,又在区间![]() 上单调递减的是 ( )
上单调递减的是 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
6.等比数列![]() 中,若对任意正整数
中,若对任意正整数![]() ,有
,有![]() ,则
,则![]() A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() ( )
( )
7.
|
A.![]() B.
B.![]()
C.![]() D.
D.![]()
8.已知等差数列![]() ,
,![]() 表示前
表示前![]() 项的和,
项的和,![]() 则
则![]() 中最小的是( )
中最小的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9.若函数![]() 反函数,则实数m的取值范围是 ( )
反函数,则实数m的取值范围是 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
10.已知函数![]() 满足:①
满足:①![]() ;②在
;②在![]() 上递增;③
上递增;③![]() ,
, ![]() 且
且![]() ,则
,则![]() 与
与![]() 的大小关系为 ( )
的大小关系为 ( )
A.![]() B.
B.![]()
C.![]() D.无法确定
D.无法确定
11.已知函数![]() 的解集是
的解集是![]() ,则
,则
![]() 的解集是 ( )
的解集是 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
 12. 已知
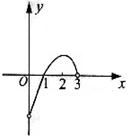
12. 已知![]() 的定义在(-3,3)上的奇函数,当0<x<3时,
的定义在(-3,3)上的奇函数,当0<x<3时,![]() 的图象如图所示,那么不等式
的图象如图所示,那么不等式![]() 的解集是
的解集是
A.![]() B.
B.![]()
C.![]() D.
D.![]()
![]()
第Ⅱ卷(非选择题 共100分)
二、填空题:本大题共4小题,每小题4分,共16分.把答案填在答题卷中相应的横线上.
13.若![]() ,则
,则![]() = .
= .
14.已知函数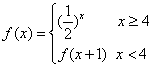 ,则
,则![]() 的值为_________.
的值为_________.
15.若![]() 是函数
是函数![]() 图象上任意不同的两点,那么直线PQ的斜率的取值范围为_______.
图象上任意不同的两点,那么直线PQ的斜率的取值范围为_______.
16.观察下表中的数字排列规律,第n行(![]() )第2个数是__________.
)第2个数是__________.

三、解答题
17.设函数![]() 图像的一条对称轴是直线
图像的一条对称轴是直线![]() 。
。
(Ⅰ)求![]() ;
;
(Ⅱ)求函数![]() 的单调增区间;
的单调增区间;
(Ⅲ)证明直线![]() 与函数
与函数![]() 的图像不相切。
的图像不相切。
18.学校近期对学生的某个体育项目进行测试,每个同学最多有4次参加测试的机会,只要有一次测试合格就算过关.如果某同学参加4次测试,合格的概率依次为0.5,0.6,0.7,0.8.求该同学参加测试次数![]() 的分布列和
的分布列和![]() 的期望,并求该同学能通过测试的概率.
的期望,并求该同学能通过测试的概率.
19.已知![]() .
.
(I)求sinx-cosx的值;
(Ⅱ)求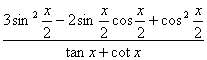 的值.
的值.
20. 已知数列{![]() }满足
}满足![]() ,且
,且![]() .
.
(Ⅰ)求证:数列![]() 是等差数列; (Ⅱ)求数列
是等差数列; (Ⅱ)求数列![]() 的通项公式;
的通项公式;
(Ⅲ)设数列![]() 的前
的前![]() 项之和
项之和![]() .
.
21.已知函数![]() 在
在![]() 处的切线方程为
处的切线方程为 ![]() ,
,
(Ⅰ)若函数![]() 在
在![]() 时有极值,求
时有极值,求![]() 的表达式;
的表达式;
(Ⅱ)在(Ⅰ)条件下,若函数![]() 在
在![]() 上的值域为
上的值域为![]() ,求m的取值范围;
,求m的取值范围;
(Ⅲ)若函数![]() 在区间
在区间![]() 上单调递增,求b的取值范围.
上单调递增,求b的取值范围.
22.已知函数![]() 的图象过点
的图象过点![]() ,且方程
,且方程![]() 有两个相等的实数根.
有两个相等的实数根.
(Ⅰ)求实数![]() 的值;
的值;
(Ⅱ)若正项数列![]() 满足:
满足:![]() ,求通项
,求通项![]() ;
;
(Ⅲ)对满足(2)中的数列![]() ,若数列
,若数列![]() ,
,![]() 为数列
为数列![]() 的前
的前![]() 项和,证明
项和,证明![]() .
.
参考答案
一、选择题(本大题共10小题,每小题5分,共50分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | B | C | C | B | C | C | C | B | D | C | A | B |
二、填空题(本大题共4小题,每小题6分,共36分)
13. ![]() 14.
14.![]()
15.![]() 16.
16.![]()
17.解答:
(Ⅰ)![]() 的图像的对称轴,
的图像的对称轴,![]()
![]()
![]()
(Ⅱ)由(Ⅰ)知![]()
由题意得
![]()
所以函数![]()
(Ⅲ)证明:![]()
所以曲线![]() 的切线斜率取值范围为[-2,2],而直线
的切线斜率取值范围为[-2,2],而直线![]() 的斜率为
的斜率为![]() ,所以直线
,所以直线![]() 与函数
与函数![]() 的图像不相切.
的图像不相切.
18.解答:某同学参加测试次数![]() 的分别列为
的分别列为
|
| 1 | 2 | 3 | 4 |
| 概率P |
|
|
|
|
-------8分
![]() 的期望为
的期望为![]() --------3分
--------3分
该同学能通过测试的概率为![]() -------3分
-------3分
19. (I)由已知:![]() 又
又![]() ,
,
![]() =
=![]() 。
------------ 6分
。
------------ 6分
(Ⅱ)由(I)得: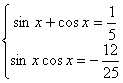 。
。
原式=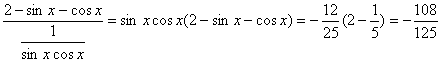 。
。
------------ 12分
20.解答: ![]()
![]()
![]() -------4分
-------4分
![]()
![]() -------4分
-------4分
![]() ……①
……①
![]() ……②
……②
②-①![]()
![]()
![]() -------6分
-------6分
21.解答:由![]() 求导得
求导得![]() ,在
,在![]() 处的切线方程为
处的切线方程为![]() 即
即![]()
由已知切线方程为![]()
所以:![]() 即
即![]()
![]()
![]()
![]()
![]() -------4分
-------4分
(2)![]()
| x | -2 |
|
|
|
|
| - | - | 0 | + |
|
| 13 | ↘ | 极小 | ↗ |
![]() ,
,![]()
当![]() ,令
,令![]() 得
得![]() ,由题意得m的取值范围为
,由题意得m的取值范围为![]() -------5分
-------5分
(3)![]() 上单调递增
上单调递增
又![]() ,
,![]()
依题意![]() 上恒成立
上恒成立![]()
①在![]()
②在![]()
![]()
③在![]()
22.(1)∵函数![]() 的函数图象过点
的函数图象过点![]() ,
,
∴函数![]() 的图象过点
的图象过点![]() ,则
,则![]() 。
。
又∵方程![]() 有两个相等的实数根,
有两个相等的实数根,
∴![]() ,即方程有等根
,即方程有等根![]() ,则
,则![]()
代入![]() 得
得![]() ,故
,故![]() 。
-------4分
。
-------4分
(2)∵![]() ,∴
,∴![]() ,即
,即![]()
∴![]() ,则
,则![]() -------4分
-------4分
(3)![]() ,所以
,所以![]()
∵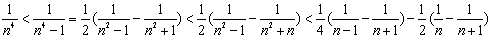
∴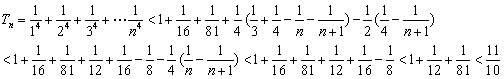
-------6分