高三数学试卷(理科)
一. 选择题 (本题共10小题,每小题5分,满分50分)
1、设全集![]() ,集合
,集合![]() ,
,![]() ,则
,则![]() =( )
=( )
(A) ![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D) ![]()
2、已知![]() ,且
,且![]() , 则
, 则![]() = ( )
= ( )
(A) ![]() (B)
(B)
![]() (C)
(C) ![]() (D)
(D)
![]()
3、过定点![]() 的直线被圆C:
的直线被圆C:![]() 所截,所截得的最短弦长为( )
所截,所截得的最短弦长为( )
(A) ![]() (B)
(B)
![]() (C)
(C)
![]() (D)
(D)
![]()
4、已知函数![]() 的反函数为
的反函数为![]() ,若
,若![]() ,则
,则![]() 的最小值是( )
的最小值是( )
(A)
1
(B) ![]() (C)
(C) ![]() (D)
(D)
![]()
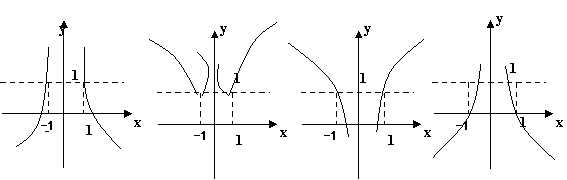 5、函数
5、函数![]()
![]() 的图象大致是( )
的图象大致是( )
(A) (B) (C) (D)
6、数列![]() 中,
中,![]() ,则下列值中满足
,则下列值中满足![]() 的
的![]() 值是( )
值是( )
(A) 20 (B) 19 (C) 18 (D) 17
7、已知函数![]() .在
.在![]() 上单调递减,则实数
上单调递减,则实数![]() 的取值范围是( )
的取值范围是( )
(A) ![]() (B)
(B)
![]() (C)
(C)
![]() (D)
(D)
![]()
8、在![]() 中,
中,![]() 是
是![]() 的( )
的( )
(A)充分而不必要条件 (B)必要而不充分条件 (C)充要条件 (D)既非充分也非必要条件
9、设点![]() 是曲线
是曲线![]() 上任一点,
上任一点, ![]() 点处切线的倾斜角为
点处切线的倾斜角为![]() ,则
,则![]() 的取值范围是( )
的取值范围是( )
(A) ![]() (B)
(B) ![]() (C)
(C) ![]()
![]() (D)
(D) ![]()
10.若一些函数的解析式和都相同,但定义域不同,我们称这些函数为“同族函数”.那么函数解析式为 ![]() 、值域为
、值域为![]() 的“同族函数”中不同函数个数有( )
的“同族函数”中不同函数个数有( )
(A) 15 (B) 16 (C) 27 (D) 81
二.填空题 (本大题共4小题,每小题4分,满分16分)
11.定义运算![]() ,满足条件
,满足条件![]() 的复数
的复数![]() = .
= .
12.已知![]() 的展开式中,所有项的系数之和等于81,那么这个展开式中
的展开式中,所有项的系数之和等于81,那么这个展开式中![]() 的系数是
。
的系数是
。
13.已知![]() 满足约束条件
满足约束条件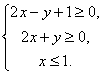 ,则
,则![]() 的最小值是 。
的最小值是 。
14.已知曲线C的方程:![]() ,则下列结论正确的是
,则下列结论正确的是
(请将你认为正确的结论序号全部填入)
①曲线![]() 关于
关于![]() 轴对称;
②曲线
轴对称;
②曲线![]() 关于原点对称;
关于原点对称;
③点![]() 都在曲线C上; ④曲线
都在曲线C上; ④曲线![]() 是封闭图形,且面积大于
是封闭图形,且面积大于![]()
三、解答题(本大题共6小题,每小题14分,共84分。解答写出文字说明,证明过程或演算步骤。)
15、已知函数![]() 。
。
(1)求函数![]() 的最小正周期和单调递增区间;
的最小正周期和单调递增区间;
(2)将函数![]() 的图象按向量
的图象按向量![]() 平移,使平移后的图象关于原点成中心对称,求长度最小的
平移,使平移后的图象关于原点成中心对称,求长度最小的![]()
16、已知函数![]() 是定义在
是定义在![]() 上的奇函数,且当
上的奇函数,且当![]() 时都有
时都有![]() 成立,
成立,
(1)若![]() ,试比较
,试比较![]() 与
与![]() 的大小;(2)若对
的大小;(2)若对![]() ,
,![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围。
的取值范围。
17、![]() 袋中有写有数字0的卡片2张,数字1的卡片3张,
袋中有写有数字0的卡片2张,数字1的卡片3张,![]() 袋中有写有数字0的卡片2张,数字1的卡片1张,现从
袋中有写有数字0的卡片2张,数字1的卡片1张,现从![]() 袋、
袋、![]() 袋中各任取一张卡片,交换后放回。
袋中各任取一张卡片,交换后放回。
(1)求交换后,![]() 袋中仍保持数字0的卡片2张,数字1的卡片3张的概率;
袋中仍保持数字0的卡片2张,数字1的卡片3张的概率;
(2)交换后,![]() 袋中所有的卡片上的数字之和记为
袋中所有的卡片上的数字之和记为![]() ,求
,求![]() 的分布列及数学期望。
的分布列及数学期望。
18、一次函数![]() 满足
满足![]() ,点
,点![]() 在函数
在函数![]() 的图象上,并有
的图象上,并有![]()
![]() 。
。
(1)求数列![]() 的通项公式;
的通项公式;
(2)记![]() ,求
,求![]() 。
。
19、已知![]() 是椭圆
是椭圆![]() 的左、右焦点,
的左、右焦点,![]() 为坐标原点,动点
为坐标原点,动点![]() 满足
满足![]() ,
,
(1)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)过椭圆的右焦点![]() 作倾斜角为
作倾斜角为![]() 的直线与轨迹
的直线与轨迹![]() 交于
交于![]() 两点,问在椭圆左准线上是否存在点
两点,问在椭圆左准线上是否存在点![]() ,使
,使![]() 为锐角三角形? 若存在,求点
为锐角三角形? 若存在,求点![]() 纵坐标的取值范围;若不存在,说明理由。
纵坐标的取值范围;若不存在,说明理由。
20、函数![]() 在
在![]() 与
与![]() 处取得极值,且
处取得极值,且![]() ,曲线
,曲线![]() 与直线
与直线![]() 相切于原点,
相切于原点,
(1)用![]() 表示
表示![]() ;
;
(2)求实数![]() 的最大值;
的最大值;
(3)若函数![]() ,其中
,其中![]() 是
是![]() 的导函数,证明:当
的导函数,证明:当![]() ,且
,且![]() 时,
时,![]() 。
。
高三数学(理科)答案
一、
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | A | C | C | B | A | B | B | C | D | D |
二、 11、![]() 12、32 13、
12、32 13、![]() 14、①②④
14、①②④
三、
15、解:
![]()
![]()
(1)![]() ,函数的单调递增区间为
,函数的单调递增区间为![]()
(2)由![]() ,得
,得![]() ,于是
,于是![]()
![]() ,
,
当![]() 时,
时,![]() 最小,此时
最小,此时![]()
![]() 。
。
16、解:(1)因为函数![]() 是定义在
是定义在![]() 上的奇函数,所以
上的奇函数,所以![]() ,
,
由![]() ,得
,得![]() ,又
,又![]() ,所以
,所以![]() 。
。
(2)由题意,对![]() ,
,![]() 恒成立,得
恒成立,得
![]() ,即
,即![]() ,
,
又因为![]() ,都有
,都有![]() ,即
,即![]() 是
是![]() 上的增函数,
上的增函数,
从而![]() 对
对![]() 恒成立
恒成立![]()
![]() 对
对![]() 恒成立,
恒成立,
![]() .即实数
.即实数![]() 的取值范围为
的取值范围为![]() .
.
17、解:(1)![]()
(2)
|
| 2 | 3 | 4 |
|
|
|
|
|
![]()
![]()
18、解:(1)设![]() ,由
,由![]() 得
得![]()
又点![]() 在函数
在函数![]() 的图象上,得
的图象上,得
![]() ,
,![]()
![]() ,从而
,从而![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
19、解:(1) ![]() ,
,![]() ,
,![]()
由![]()
![]() ,化简得轨迹
,化简得轨迹![]() 的方程:
的方程:![]()
(2)抛物线的 焦点为![]() ,准线
,准线![]() ,椭圆左准线:
,椭圆左准线:![]()
椭圆左准线在抛物线准线的左边,所以![]() 为锐角。
为锐角。
由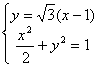
![]() 或
或![]()
即![]()
![]() ,
,![]() 、
、![]()
![]() ,
,![]() ,设
,设![]()
![]()
![]() ,
,![]()
![]() ,
,![]() 。
。
![]() 为锐角三角形,则
为锐角三角形,则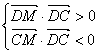
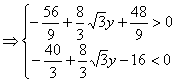
解得:![]() 。即存在点
。即存在点![]() ,使
,使![]() 为锐角三角形,且点
为锐角三角形,且点![]() 纵坐标的取值范围为
纵坐标的取值范围为![]()
20、解:(1)![]() ,
,![]() 。
。
(2)![]() 是方程
是方程![]() 的两根,
的两根,![]() ,
,
![]()
![]()
![]()
![]()
![]()
![]() ;
;![]()
令![]()
![]() ,则
,则![]() ,
,
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,![]()
![]()
(3)![]()
![]()
![]()
![]()
![]()
![]()
由![]() ,
,![]()
![]()
![]()
![]() ,
,
当![]() 时,
时,![]() ,
,![]()
![]()
![]()
![]()
![]()