高三数学综合测试（八）
一、选择题：本大题共10小题，每小题5分，共50分。在每小题给出的四个选项中，只有一项是符合题目要求的。把答案填在答卷上对应的空格内。
1．设集合
,则满足
的集合B的个数是 （ ）
A．1 B．3 C．4 D．8
2．“
”是“函数
在区间
上为增函数”的 （ ）
A．充分不必要条件 B．必要不充分条件
C．充要条件 D．既不充分也不必要条件
3．
|
,且
=
则（ ）
A．0≤
≤
B．
≤≤
C．≤≤
D．
≤≤
4．函数
的图象关于（ ）对称；
5．在正方体ABCD－A1BC1D1中，点P在线段AD1上运动，则异面直线CP与BA1所成的角
的取值范围是 ( )
A.
B.
C. 
D.
6．已知数列
的通项公式
，设的前
项的和为
，则使
成立的自然数（ ）
7. 世界杯足球赛共有24个球队参加比赛，第一轮分成六个组进行单循环赛（在同一组的每两个队都要比赛），决出每个组的一、二名，然后又在剩下的12个队中按积分取4个队（不比赛），共计16个队进行淘汰赛来确定冠亚军，则一共需比赛（ ）场次
A.53 B.52 C.51 D.50
8．若将
逐项展开得
，则
出现的频率为
，
出现的频率为
，如此将
逐项展开后，
出现的频率是（ ）
9．若
是一个给定的正整数，如果两个整数
用除所得的余数相同，则称
与
对模同余，记作
，例如：
.若:
,则
可以为（ ）
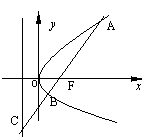10．如图，过抛物线
的焦点F的直线
交抛物线于点A、B，交其准线于点C，若
，且
，则此抛物线的方程为
( )
A．
B．
C．
D．
二、填空题：本大题共5小题，每小题5分，共25分，把答案填在题中横线上．
11、设函数
， 则使得
≥1的自变量
的取值范围是
.
12、已知复数
，
则
.
13、已知
且满足不等式组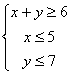
，则
的最大值是
.
14、已知动点
在椭圆
上，若
点坐标为
且
，则
的最小值是 .
15、定义运算a※b为
.如1※2=1，则函数
※
的值域为 ；若a※b为
,如1※2=2，则函数※的值域为
.
高三数学综合测试（八）
班级： 姓名： 学号：
一、选择题：本大题共10小题，每小题5分，共50分。
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
|
|
|
|
|
|
|
|
|
|
二．填空题：本大题共5小题，每小题5分，共25分。
11、 12、 13、
14、 15、
三．解答题：本大题共6小题，共75分。解答应写出文字说明，证明过程或演算步骤．
16、（本小题满分12分）
已知△ABC的面积S满足3≤S≤3
，且
·
=6，与的夹角为
（1）求的取值范围；
（2）若函数f()=sin2+2sincos+3cos2，求f()的最小值.
17、（本小题满分12分）如图，直三棱柱ABC-A1B1C1中， AC=BC，
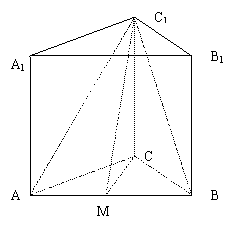且AM=BM=CM，M为AB的中点.
（1）、求证： AC1⊥CB ；
（2）、若∠AC1B=60°，求CB与平面AC1B
所成角的余弦值。
18、（本小题满分12分）在湖南卫视的一次有奖竞猜活动中，主持人准备了A、B两个相互独立的问题，并且宣布：幸运观众答对问题A可获奖金1000元，答对问题B可获奖金2000元，先答哪个题由观众自由选择，但只有第一个问题答对，才能再答第二题，否则终止答题。若你被选为幸运观众，且假设你答对问题A、B的概率分别为、。
(1)、记先回答问题A的奖金为随机变量
，则的取值分别是多少？
(2)、你觉得应先回答哪个问题才能使你获得更多的奖金？请说明理由.
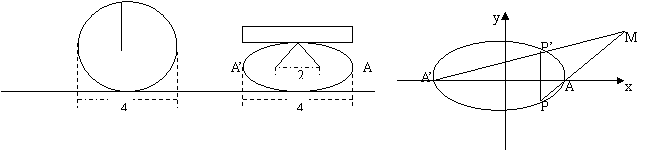
19. （本小题满分12分）如图：半径为2的圆，在外力下压成椭圆，圆心“弹开”，半径裂成两条（长度不变）；
（1）、求椭圆的标准方程；
（2）、过该椭圆外一点
，连接
与
分别交椭圆于不同两点
与
，且与关于轴对称，求点的轨迹方程。
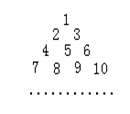20.（本小题满分13分）把正整数按上小下大，左小右大的原则排成三角形数表示（每一行比上一行多一个数），如右图所示：设
是位于这个三角形数表中从上往下数第
行，从左往右数第
个数，如
.
（1）
若
，求
的值；
（2）
记三角形数表从上往下数第行各数之和为
，
令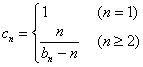
，若数列
的前项和为
，求
的值。
21.（本小题满分14分） 定义函数
其导函数记为
.
（1）、求证：
；
（2）、设
，求证：
；
（3）、是否存在区间
使函数
在区间
上的值域为
？ 若存在，求出最小的
值及相应的区间.