高考数学（理科）模拟试题（二）
第Ⅰ卷
一、选择题：本大题共8小题，每小题5分，共40分，在每小题给出的四个选项中，只有一项是符合题目要求的．
1．设P、Q为两个非空实数集合，定义集合
若P={0.2.5}Q={1,2,6}则P+Q元素的个数是（ ）
Ａ．6 Ｂ．7 Ｃ．8 Ｄ．9
2．设P、Q是简单命题，则“P且Q为假”是“P或Q为假”的 ( )
Ａ．必要不充分条件 Ｂ．充分不必要条件
Ｃ．充要条件 Ｄ．既不充分也不必要条件
3． 下列问题的算法适宜用条件结构的是( )
Ａ．求点(1,0)到点(3,4)的距离 Ｂ．已知直角三角形两直角边求斜边
Ｃ．计算1,3,5,7,9这5个数的平均数 Ｄ．解不等式
4． 若复数
为实数,则实数m的值为( )
Ａ．
Ｂ．
Ｃ．或 Ｄ．以上都不对
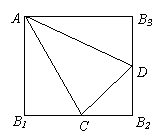5．如图，正方形AB1 B2 B3中，C，D分别是B1 B2 和B2 B3
的中点，现沿AC，AD及CD把这个正方形折成一个四面体，
使B1 ，B2 ，B3三点重合，重合后的点记为B，则四面体
A—BCD中，互相垂直的面共有（ ）
Ａ．4对 Ｂ．3对
Ｃ．2对 Ｄ．1对
6．对于
上可导的任意函数
，若满足
，则必有（ ）
Ａ．
B.
C．
D．
7．已知等差数列
的前
项和为
，若
，且
三点共线（该直线不过点
），则
等于（ ）
Ａ．100 Ｂ．101 Ｃ．200 Ｄ．201
8.若函数
在区间
内恒有
,则
的单调递增区间是( )
Ａ.
Ｂ.
Ｃ.
Ｄ.
第Ⅱ卷
二、填空题：本大题6小题，每小题5分，共30分．
9. 下图是一个物体的三视图,根据图中尺寸(单位:cm),计算它的体积 (结果精确到1 cm3) 等于 cm3．
 |
10．在
的二项展开式中，若常数项为
，则等于 ．
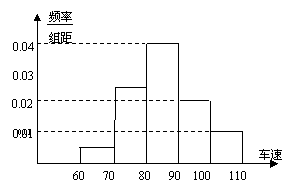
11．在某路段检测点,对200辆
汽车的车速进行检测,检测结果
表示为如图所示的频率分布直
方图,则车速不小于90 km/ h的
汽车有 辆．
12. 
为双曲线
的右支上一点，
，
分别是圆
和
上的点，则
的最大值为 .
13,14.在下列三题中选做两题(若三题都做,则以得分较低的两题计分):
(1)如图为一物体的轴截面图,则图中R的值是 ．
 |
(2) 已知直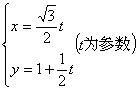线
与抛物线
交于A、B两点，则线段AB的长是 ．
（3）若
，则
的最小值是 ．
三、解答题：本大题共6小题，共80分．解答应写出文字说明，证明过程或演算步骤．
15．（本小题满分12分）
已知函数
(1) 画出函数的简图;
(2) 该函数是周期函数吗?若是,它的最小正周期是多少?
(3) 写出这个函数的单调增区间.
16．（本小题满分12分）
某班有学生45人,其中O型血的人有10人,A 型血的人有12人, B型血的人有8人,AB 型血的人有15人,现抽取两人进行检验,
(1) 求这两人血型相同的溉率;
(2) 求这两人血型相同的分布列.
17．（本小题满分14分）
如图,已知长方体AC1中,棱AB=BC=1, BB1=2, 连接B1C, 过B点作B1C的垂线交CC1于E, 交B1C于F.
(1) 
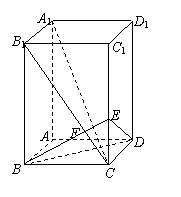求证: A1C⊥平面EBD;
(2) 求点 A到平面A1B1C的距离;
(3) 求平面A1B1C与直线DE所成角的正弦值.
18．（本小题满分14分）
设抛物线
与直线
的两交点为A、B，点P在抛物线的弧上从A向B运动，
（1） 求使△PAB的面积最大时P点的坐标
；
（2） 证明由抛物线与直线围成的图形被直线
分成面积相等的两部分.
19．（本小题满分14分）
已知二次函数
,
(1) 若
且
,证明:的图像与x轴有两个相异交点;
(2)
证明:
若对x1, x2, 且x1<x2,
,则方程
必有一实根在区间 (x1, x2)
内;
(3)
在(1)的条件下,是否存在
,使
成立时,
为正数.
20．（本小题满分14分）
设F1, F2分别为椭圆
的左右两个交点.
(1) 若椭圆C上的点
到F1, F2两点的距离之和等于4, 写出椭圆C的方程和焦点坐标;
(2)
设点K是(1)中所得椭圆上的动点,求线段
的中点的轨迹方程;
(3)
已知椭圆具有性质: M,N是椭圆C上关于原点对称的两个点, 点P是椭圆上任意一点,当直线PM, PN的斜率都存在,并记为
,
时,那么与之积是与点P位置无关的定值.试对双曲线
写出类似的性质,并给以证明.
参考答案:
一、BADC BDAC
二、9．457 10.6 11.60 12.9 13、14.(1)25 (2)
(3)3
三、
15.解(1) 
(图象略).
(2)由图象知函数的最小正周期是
.
(3) 由图象知函数的单调增区间是
(1) 16．解(1)记两人血型同为O,A,B,AB型的概率分别为P1,P2,P3,P4,则
故两人血型相同的概率为
(2)将两人血型同为O,A,B,AB型编号为1,2,3,4, 记两人血型相同为X,则 X的可能取值为1,2,3,4,其分布列为:
X | 1 | 2 | 3 | 4 |
P | 45/244 | 33/122 | 7/61 | 105/244 |
17．. 解:如图
|
(1)证明略
(2)
(3)
18．解(1)令
得
,
.此时△PAB的面积最大,故 P点的坐标为
(2)提示:由定积分求得两部分面积都等于
19．解(1) 提示:可推出
.
(2) 提示:可令
.证明
.
(3)略解: 假设存在符合条件的,则由已知得
且
.由(1)知
,故有
.
,
.
令
,可推得
的对称轴
.
故在
上有零点.
即方程必有一根
.
进而推得当
时,
.
20．(1)椭圆C的方程为
,焦点坐标
.
(2)所求轨迹方程为
.
(3)类似的性质为: 若M,N是双曲线上关于原点对称的两个点, 点P是椭圆上任意一点,当直线PM, PN的斜率都存在,并记为,时,那么与之积是与点P位置无关的定值..
证明:设点M的坐标为
,则点N的坐标为
,其中
.
又设点P的坐标为
,
由 
得
,
将 
代入得
.