高考数学（理科）模拟试题（四）

高考数学（理科）模拟试题（四）

一、选择题：（每小题5分，共40分）

1、设集合U={1,2,3,4,5},A={1,3,5},B={2,3,5},则C_U(A∩B)等于(　　 )

(A) {1,2,4}　　　 (B){4}　　　 (C) {3,5}　　  (D)Ф

2、已知sin=，sin<0,则tan的值等于(  　  )

(A) 　　　　(B)　　  (C)　　　　(D)

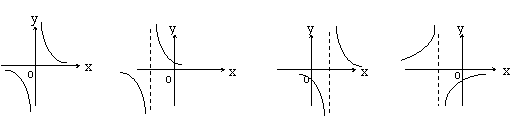
3、函数的大致图象只能是（  　　）

（A）　　　　　　 (B)　　　　　　  (C)　　　　　　　  (D)

4、双曲线的两条准线分顶点间距离为三等分，则双曲线的离心率为(  　  )

(A) 　　　　　(B)3　　　　　 (C)　　　　  (D)6

5、设A=，B=,若AB，则实数的取值范围是(  　  )

(A)　　 (B)　　 (C)　　 (D)

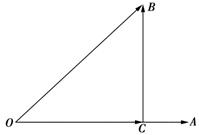
6．如图，非零向量,且BC⊥OA，C为垂足，设向量a，则λ的值为t(　　　)（（（

  A.　　　　　　　　　 B.

　C.　　　　　　　　　 D.

7、已知直线平面，直线平面，给出下列命题：

若∥，则　　　　 ②若，则∥

③若∥，则　　　　 ④若，则∥

其中正确的命题是（  　　）

（A）③④　　 （B）①③　　 （C）②④　　 （D）①②

8、在某次数学测验中，记座号为的同学的考试成绩为，

若，且满足，则这四位同学考试成绩的所有可能情况有（　　　）种　

(A)15　　　 (B)20　　　(C)30　　　  (D)35

二、填空题：（每小题5分，共30分）

9、若与的夹角为150­⁰，，则　　　　

10、抛物线的焦点坐标是，则　　　

11、△ABC中，BC=8，AC=5，三角形面积为12，则cos2C的值为　　　　

12、　　　　　 。　　　　　　　　　　

13、一个正整数表如下（表中下一行中的数的个数是上一行中数的个数的2倍）：　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

第1行	1
第2行	2　　　　 3
第3行	4　　 5　　　 6　　 7
…	……　　　　  ……

　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 

则第9行中的第4个数是　  　　　　

14、在以下三题中选做一道

(1)过点A(2,3)的直线的参数方程，若此直线与直线

相交于点B，则＝　　　　　。

(2)已知，则的最大值为　　　　　。

(3)若BE、CF是的高，且，则＝　　　　。

三、解答题(满分80分)

15、(本小题满分14分)

已知A、B是△ABC内角，

①若A、B,求证：tanA•tanB>1，

②若B=，求sinA+sinC的取值范围。

16.(本小题满分14分)

　在一次军事演习中，某军同时出动了甲、乙、丙三架战斗机对一军事目标进行轰炸，已知甲击中目标的概率是；甲、丙同时轰炸一次，目标未被击中的概率为；乙、丙同时轰炸一次，都击中目标的概率是.

　(1)求乙、丙各自击中目标的概率；

　(2)求目标被击中的概率.

17.(本小题满分14分)

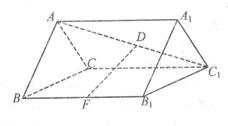  如图，正三棱柱ABC-A₁B₁C₁的各棱长都等于2，D在AC₁上，F为BB₁中点，且FD⊥AC₁，

(1)试求的值；

(2)求二面角F-AC₁-C的大小;

(3)求点C₁到平面AFC的距离.

18.(本小题满分14分)

　在平面直角坐标系中,已知A_n(n,a_n)、B_n(n,b_n)、C_n(n-1,0)(n∈N*)，满足向量与向量共线，且点B_n(n,b_n) (n∈N*)都在斜率为6的同一条直线上.

　(1)试用a₁，b₁与n来表示a_n;

  (2)设a₁=a，b₁=-a,且12<a≤15，求数列{a_n}中的最小项。

19.(本小题满分12分)

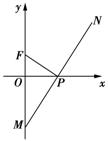
　已知定点F(0,a)(a≠0)，点P、M分别在x，y轴上，满足·＝0，点N满足＋＝0.

　(1)求N点的轨迹方程C；

　(2)过F作一条斜率为k的直线l，l与曲线C交于A、B两点，设G(0,-a),∠AGB=θ，求证：0<θ≤。

20.(本小题满分12分)

　已知函数f(x)=mx³-x的图象上，以N(1,n)为切点的切线的倾斜角为，

　(1)求m,n的值；

　(2)是否存在最小的正整数k，使得不等式f(x)≤k-1991对于x∈[-1,3]恒成立？如果存在，请求出最小的正整数k；如果不存在，请说明理由;

　(3)求证：f(sinx)+f(cosx)≤2f(t+)(x∈R，t>0).

参考答案

一．选择题

1－8　　A　B　B　B　A　A　B　A

二．填空题　

9．　2　　　　　　　　　　　10．

11．　　　　　　　　　　　12．

13．　259　　　　　　　　　　

14．(1) 　　(2)　　 (3)

三．解答题

15．①证

②解：

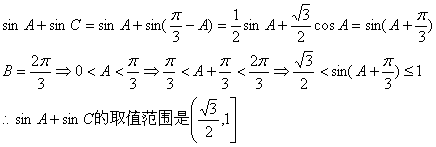
16(12分)

　 解：(1)记甲、乙、丙各自独立击中目标的事件分别为A、B、C.

　　则由已知，得P(A)=,P(·)=P()P()=[1-P(C)]=,∴P(C)=…3分

　　由P(B·C)＝P(B)P(C)=，得P(B)=，∴P(B)＝.　　　…………8分

　 (2)目标被击中的概率为

1-P(··)＝1-[1-P(A)][1-P(B)][1-P(C)]=1-(1-)(1-)(1-)=,…10分

答:(1)乙、丙各自击中目标的概率分别为，;(2)目标被击中的概率为.…12分

17.(12分)

　　解(方法1)(1)连AF，FC₁，∵三棱柱ABC-A₁B₁C₁是正三棱柱且各棱长都等于2，又F为BB₁中点，∴Rt△ABF=Rt△C₁B₁F，∴AF=FC₁.

　　　又在△AFC₁中，FD⊥AC₁，所以D为AC₁的中点，即=1.　………4分

　　(2)取AC的中点E，连接BE及DE，易得DE与FB平行且相等，

　　　 ∴四边形DEBF是平行四边形，∴FD与BE平行.

　　　 ∵三棱柱ABC-A₁B₁C₁是正三棱柱,∴△ABC是正三角形,∴BE⊥AC，∴FD⊥AC.

　　　 又∵FD⊥AC₁，∴FD⊥平面ACC₁，所以二面角F-AC₁-C的大小为90°，　…9分

　　(3)运用等积法求解，AC＝2，AF＝CF＝，可求S_△ACF＝2，

　　　 V_F-ACC1= V_B-ACC1­=××=，V_F-ACC1= V_C1-ACF=S_△ACF×h，

求得h=.12分

18.(14分)

　 解：(1)∵点B_n(n,b_n)(n∈N*)都在斜率为6的同一条直线上，

　　　　  ∴=6，即b_n+1-b_n=6,

　　　　  于是数列{b_n}是等差数列，

故b_n=b₁+6(n-1).　　　　　　　　  …………3分

∵共线.

∴1×(-b_n)-(-1)(a_n+1-a_n )=0,即a_n+1-a_n=bn　　　　　　　　　　　　　…………5分

∴当n≥2时，a_n=a₁+(a₂-a₁)+(a₃-a₂)+ …+(a_n-a_n-1)=a₁+b₁+b₂+b₃+…+b_n-1

　　　　　　　　　　  =a₁+b₁(n-1)+3(n-1)(n-2)　　　　　　　　　　　　　　　　　　　　　　　　　…………7分

当n=1时，上式也成立.

所以a_n=a₁+b₁(n-1)+3(n-1)(n-2).　　　　　　　　　　　　　　　　　　　　　　　　　　　 …………8分

(2)把a₁=a,b₁=-a代入上式，得a_n=a-a(n-1)+3(n-1)(n-2)=3n²-(9+a)n+6+2a.

∵12<a≤15,∴,∴当n=4时，a_n取最小值，最小值为a₄=18-2a. 14分

19.(14分)

解：(1)∵，∴P为MN的中点.

　　　 　　设N(x,y)，则M(0，-y),P().

　　　 　　于是()，.

　　　　∵∴()²-ay=0.

即N点的轨迹方程为x²=4ay　　　　　　　　　　　　　　　　　　　　　　　　　………5分

(2)由题意知，直线l的方程为y=kx+a,代入x²=4ay得x²-4akx-4a²=0.

　设A(x₁,y₁),B(x₂,y₂),则x₁+x₂=4ak,x₁x₂=-4a^2. 　　　　　　　　　　　　　　　　　 ………7分

　∴y₁+y₂=(kx₁+a)+(kx₂+a)=k(x₁+x₂)+2a=4ak²+2a,

　y₁y₂=(kx₁+a)(kx₂+a)=k²x₁x₂+ak(x₁+x₂)+a²=-4a²k²+4a²k²+a²=a²　　　　　　 …9分

　∵G(0，-a),∴=(x₁,y₁+a),(x₂,y₂+a).

　∴=x₁x₂+(y₁+a)(y₂+a)=x₁x₂+y₁y₂+a(y₁+y₂)+a²

　  =-4a²+a²+a(4ak²+2a)+a²=4a²k²≥0,

即·cosθ≥0，∴cosθ≥0,故0≤θ≤.　　　　　　　　　　　　 ……12分

又点G(0，-a)不在直线l上，∴A、B、G三点不共线.

故0<θ≤.　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 ………14分

20.(14分)

　解：(1)f′(x)=3mx²-1,依题意，得tan= f′(1)，即1=3m-1,m=.

　　　 　∴f′(x)=,n=－.

　　　 　(2)令f′(x)=2x²-1=0,得x=±.

　　　 　当-1<x<-时，f′(x)=2x²-1>0;

　　　 　当<x<3时，f′(x)=2x²-1>0.

　　　 　又f(-1)=,f(-)=,f()=-,f(3)=15.

　　　 　因此，当x∈[-1,3]时-≤f(x)≤15;　　　　　　　　　　　　　　　　………6分

　　　 　要使得不等式f(x)≤k-1991对于x∈[-1,3]恒成立，则k≥１５+1991=2006. ………8分

所以，存在最小的正整数k=2006,使不得等式f(x)≤k-1991对于x∈[-1,3]恒成立.

　　　  (3)(方法1)：f(sin)+f(cosx)=(sin³x-sinx)+(cos³x-cosx)

　　　　　　　　　　　　　　=(sin³x+cos³x)-(sinx+cosx)

　　　　　　　　　　　　　　=(sinx+cosx)[(sin²x-sinxcosx+cos²x)-1]

　　　　　　　　　　　　　　=sinx+cosx·-sinxcosx-=sinx+cosx³

　　　　　　　　　　　　　　=³≤.　　　　　　　　　　　　　　　　　　 ………11分

又∵t>0,∴t+≥

∴2f(t+)[(t2+)-≥]2.

综上可得，f(sinx)+f(cosx)≤2f(t+)(x∈R,t>0).　　　　　　　　 ………14分

(方法2)由(2)知，函数f(x)在[-1,-]上是增函数；在[-,]上是减函数；在[，1]上是增函数；

又f(-1)=,f

　　　 所以，当x∈[-1,1]时，-≤f(x)≤,即f(x)≤.

　　　 ∵sinx,cosx∈[-1,1],∴f(sinx) ≤,f(cosx)≤.

　　　 ∴f(sinx)+f(cosx) ≤f(sinx)+f(cosx) ≤+≤　　　　　　　　 ………11分

　　　 又∵t>0.∴t+且函数f(x)在[1，+∞]上是增函数.

　　　 ∴2f(t+)≥2f()=2[()³-]=.

　　　 综上可得，f(sinx)+f(cosx)≤2f(t+)(x∈R,t>0).　　　　　　　　 ………14分