高考数学(理科)模拟试题(一)
第Ⅰ卷(选择题 共40分)
一、选择题(每小题5分,满分40分)
1. 设方程![]() 的解集为A,方程
的解集为A,方程![]() 的解集为B,若
的解集为B,若![]() ,
,
则p+q= ( )
A、2 B、0 C、1 D、-1
2. 已知![]() ,且
,且![]() 是第四象限的角,则
是第四象限的角,则![]() ( )
( )
A ![]() B
B
![]() C
C ![]() D
D
![]()
3. 已知![]() 的实根个数是
( )
的实根个数是
( )
A、1个 B、2个 C、3个 D、1个或2个或3个
4.实数![]() 是直线
是直线![]() 和
和![]() 平行的(
)
平行的(
)
A.充分非必要条件 B.必要非充分条件 C.充要条件 D.既非充分也非必要条件
5.平面上有一个△ABC和一点O,设![]() ,又OA、BC的中点分别为D、E,则向量
,又OA、BC的中点分别为D、E,则向量![]() 等于(
)
等于(
)
A.![]() B
B ![]() C
C ![]() D
D ![]()
6. 函数![]() 在下面哪个区间内是增函数( )
在下面哪个区间内是增函数( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
7.点![]() 是椭圆
是椭圆![]() (
(![]() 上的任意一点,
上的任意一点,![]() 是椭圆的两个焦点,且∠
是椭圆的两个焦点,且∠![]() ,则该椭圆的离心率的取值范围是
( )
,则该椭圆的离心率的取值范围是
( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
|
 8. 已知函数
8. 已知函数A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
第Ⅱ卷
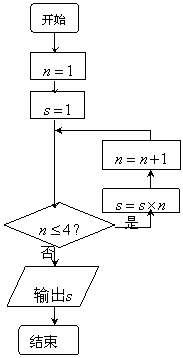 二、填空题(每小题5分,满分30分)
二、填空题(每小题5分,满分30分)
9.复数![]() (
(![]() 是虚数单位)的实部为
是虚数单位)的实部为
10.在![]() 的展开式中,
的展开式中, ![]() 的系数是
的系数是
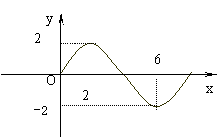
11. 函数![]() 的部分图象
的部分图象
如图1所示,则![]()
12. 程序框图(如图2)的运算结果为
13. 从以下两个小题中选做一题(只能做其中一个,做两个
按得分最低的记分).
(1)自极点O向直线l作垂线,垂足是H(![]() ),
),
|
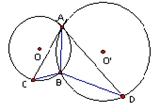
|
的切线,交⊙O于点C,AD是⊙O的切线,交⊙![]() 于
于
点D,若BC= 2,BD=6,则AB的长为
|
①0<b<a ②a<b<0 ③0<a<b ④b<a<0
⑤a=b
其中不可能成立的关系式有_______________.
三、解答题
15.(本小题满分12分)
已知函数![]() ,(1)求函数
,(1)求函数![]() 的最小正周期;(2)求函数
的最小正周期;(2)求函数![]() 的单调减区间;(3)画出函数
的单调减区间;(3)画出函数![]() 的图象,由图象研究并写出
的图象,由图象研究并写出![]() 的对称轴和对称中心.
的对称轴和对称中心.
|
| |||||||||||||||||||||
|
| |||||||||||||||||||||
|
|
|
| |||||||||||||||||||
|
|
| ||||||||||||||||||||
|
| |||||||||||||||||||||
16.(本小题满分14分)
一个盒子里装有标号为1,2,3,![]() ,
,![]() 的
的![]() (
(![]() 且
且![]() )张标签,今随机地从盒子里无放回地抽取两张标签,记ξ为这两张标签上的数字之和,若ξ=3的概率为
)张标签,今随机地从盒子里无放回地抽取两张标签,记ξ为这两张标签上的数字之和,若ξ=3的概率为![]() 。(1)求
。(1)求![]() 的值;(2)求ξ的分布列;(3)求ξ的期望。
的值;(2)求ξ的分布列;(3)求ξ的期望。
17.(本小题满分14分)
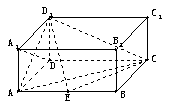
如图,在长方体![]() 中,
中,![]() ,点E在棱
,点E在棱![]() 上移动。
上移动。
(Ⅰ)证明:![]() ;
;
(Ⅱ)当E为![]() 的中点时,求点E到面
的中点时,求点E到面![]() 的距离;
的距离;
(Ⅲ)![]() 等于何值时,二面角
等于何值时,二面角![]() 的大小为
的大小为![]() 。
。
18.(本小题满分14分)
已知函数![]() .
.
①若![]() 使
使![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
②设![]() ,且
,且![]() 在
在![]() 上单调递增,求实数
上单调递增,求实数![]() 的取值范围.
的取值范围.
19.(本小题满分14分)
在平面直角坐标系内有两个定点![]() 和动点P,
和动点P,![]() 坐标分别为
坐标分别为![]() 、
、![]() ,动点
,动点![]() 满足
满足![]() ,动点
,动点![]() 的轨迹为曲线
的轨迹为曲线![]() ,曲线
,曲线![]() 关于直线
关于直线![]() 的对称曲线为曲线
的对称曲线为曲线![]() ,直线
,直线![]() 与曲线
与曲线![]() 交于A、B两点,O是坐标原点,△ABO的面积为
交于A、B两点,O是坐标原点,△ABO的面积为![]() ,
,
(1)求曲线C的方程;(2)求![]() 的值。
的值。
20.(本小题满分12分)
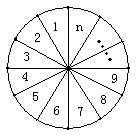
如图,将圆分成![]() 个区域,用3种不同颜色给每一个区域染色,要求相邻区域颜色互异,把不同的染色方法种数记为
个区域,用3种不同颜色给每一个区域染色,要求相邻区域颜色互异,把不同的染色方法种数记为![]() 。求
。求
(Ⅰ)![]() ;
;
(Ⅱ)![]() 与
与![]() 的关系式;
的关系式;
(Ⅲ)数列![]() 的通项公式
的通项公式![]() ,并证明
,并证明![]() 。
。
参考答案
一、选择题
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 答案 | C | A | B | C | B | B | A | D |
二、填空题
9.![]() 10。
10。![]() 11。
11。![]() 12。
12。![]() 13。(1)
13。(1)![]() (2)
(2)![]()
14.34
三、解答题
15. 解: (1)![]()
![]()
(2)由![]() 得
得![]() ,
,
所以,减区间为![]()
(3) ![]() 无对称轴,对称中心为(
无对称轴,对称中心为(![]() )
)
16.
解:(1)![]() ,
,![]()
![]()
![]()
![]() ;
;
(2) ξ的值可以是![]()
![]() ;
;![]() ;
;![]() ;
;
![]() ;
; ![]() ;
;
![]() ;
;![]() 。
。
分布列为
| ξ | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| P |
|
|
|
|
|
|
|
(3)
Eξ=![]()
![]() Eξ=
Eξ=![]() 。
。
17. 解:以D为坐标原点,直线![]() 分别为
分别为![]() 轴,建立空间直角坐标系,设
轴,建立空间直角坐标系,设![]() ,则
,则![]() 。
。
(Ⅰ)因为![]() ,所以
,所以![]() 。
。
(Ⅱ)因为E为![]() 中点,则
中点,则![]() ,从而
,从而![]() ,
,![]() ,设平面
,设平面![]() 的法向量为
的法向量为![]() ,则
,则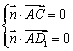 ,也即
,也即![]() ,得
,得![]() ,从而
,从而![]() ,
,
所以点E到平面![]() 的距离为
的距离为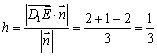
(Ⅲ)设平面![]() 的法向量为
的法向量为![]() ,
,
∵![]()
由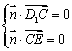 ,有
,有![]() ,令
,令![]() ,从而
,从而![]()
∴![]()
由题意,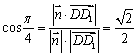 ,即
,即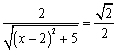 。
。
∴![]() (不合题意,舍去),
(不合题意,舍去),![]() 。
。
∴当![]() 时,二面角
时,二面角![]() 的大小为
的大小为![]() 。
。
18. 1![]() ,
,![]()
![]() ,
,![]()
![]()
2![]() ,
,![]()
(Ⅰ)当![]() 即
即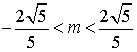 时,
时,
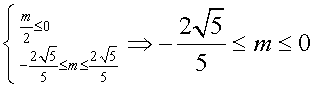
(Ⅱ)当![]() 即
即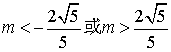 时.设方程
时.设方程![]() 的根为
的根为![]()
若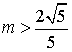 ,则
,则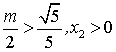 .
.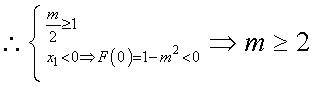
若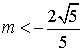 ,则
,则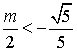
![]()
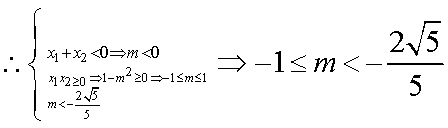
综上所述:![]()
19.解:(1)设P点坐标为![]() ,则
,则
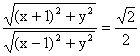 ,化简得
,化简得![]() ,
,
所以曲线C的方程为![]() ;
;
(2)曲线C是以![]() 为圆心,
为圆心,![]() 为半径的圆 ,曲线
为半径的圆 ,曲线![]() 也应该是一个半径为
也应该是一个半径为![]() 的圆,点
的圆,点![]() 关于直线
关于直线![]() 的对称点的坐标为
的对称点的坐标为![]() ,所以曲线
,所以曲线![]() 的方程为
的方程为
![]() ,
,
该圆的圆心![]() 到直线
到直线![]() 的距离
的距离![]() 为
为
![]() ,
,
![]()
![]() ,或
,或![]() ,
,
所以,![]() ,或
,或![]() 。
。
20. 解:(Ⅰ) 当![]() 时,不同的染色方法种数
时,不同的染色方法种数![]() ,
,
当![]() 时,不同的染色方法种数
时,不同的染色方法种数![]() ,
,
当![]() 时,不同的染色方法种数
时,不同的染色方法种数![]() ,
,
当![]() 时,分扇形区域1,3同色与异色两种情形
时,分扇形区域1,3同色与异色两种情形
∴不同的染色方法种数![]() 。
。
(Ⅱ)依次对扇形区域![]() 染色,不同的染色方法种数为
染色,不同的染色方法种数为![]() ,其中扇形区域1与
,其中扇形区域1与![]() 不同色的有
不同色的有![]() 种,扇形区域1与
种,扇形区域1与![]() 同色的有
同色的有![]() 种
种
∴![]()
(Ⅲ)∵![]()
∴![]()
![]()
………………
![]()
将上述![]() 个等式两边分别乘以
个等式两边分别乘以![]() ,再相加,得
,再相加,得
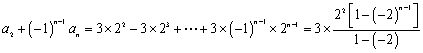 ,
,
∴![]() ,
,
从而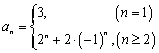 。
。
(Ⅲ)证明:当![]() 时,
时,![]()
当![]() 时,
时,![]() ,
,
当![]() 时,
时,
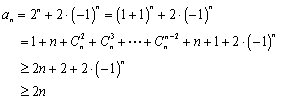 ,
,
故![]()