高考文科数学试题全国II卷
(吉林、甘肃、黑龙江、内蒙古、贵州、云南)
一.选择题
(1)已知向量![]() =(4,2),向量
=(4,2),向量![]() =(
=(![]() ,3),且
,3),且![]() //
//![]() ,则
,则![]() =( )
=( )
(A)9 (B)6 (C)5 (D)3
(2)已知集合![]() ,则
,则![]() ( )
( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
(3)函数![]() 的最小正周期是( )
的最小正周期是( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
(4)如果函数![]() 的图像与函数
的图像与函数![]() 的图像关于坐标原点对称,则
的图像关于坐标原点对称,则![]() 的表达式为( )
的表达式为( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
(5)已知![]() 的顶点B、C在椭圆
的顶点B、C在椭圆![]() 上,顶点A是椭圆的一个焦点,且椭圆的另外一个焦点在BC边上,则
上,顶点A是椭圆的一个焦点,且椭圆的另外一个焦点在BC边上,则![]() 的周长是( )
的周长是( )
(A)![]() (B)6 (C)
(B)6 (C)![]() (D)12
(D)12
(6)已知等差数列![]() 中,
中,![]() ,则前10项的和
,则前10项的和![]() =( )
=( )
(A)100 (B)210 (C)380 (D)400
(7)如图,平面![]() 平面
平面![]() ,
,![]() 与两平面
与两平面![]() 、
、![]() 所成的
所成的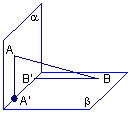 角分别为
角分别为![]() 和
和![]()
![]() 过A、B分别作两平面交线的垂线,垂足为
过A、B分别作两平面交线的垂线,垂足为![]() 、
、![]() 若AB=12,则
若AB=12,则![]() ( )
( )
(A)4 (B)6 (C)8 (D)9
(8)已知函数![]() ,则
,则![]() 的反函数为( )
的反函数为( )
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
(9)已知双曲线![]() 的一条渐近线方程为
的一条渐近线方程为![]() ,则双曲线的离心率为( )(A)
,则双曲线的离心率为( )(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
(10)若![]() 则
则![]() ( )
( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
(11)过点(-1,0)作抛物线![]() 的切线,则其中一条切线为( )
的切线,则其中一条切线为( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
(12)5名志愿者分到3所学校支教,每个学校至少去一名志愿者,则不同的分派方法共有( )(A)150种 (B)180种 (C)200种 (D)280种
二.填空题:本大题共4小题,每小题4分,共16分,把答案填在横线上
(13)在![]() 的展开式中常数项是_____
的展开式中常数项是_____![]() (用数字作答)
(用数字作答)
(14)圆![]() 是以
是以![]() 为半径的球
为半径的球![]() 的小圆,若圆
的小圆,若圆![]() 的面积
的面积![]() 和球
和球![]() 的表面积
的表面积![]() 的比为
的比为![]() ,则圆心
,则圆心![]() 到球心
到球心![]() 的距离与球半径的比
的距离与球半径的比![]() _____
_____![]()
(15)过点![]() 的直线
的直线![]() 将圆
将圆![]() 分成两段弧,当劣弧所对的圆心角最小时,直线
分成两段弧,当劣弧所对的圆心角最小时,直线![]() 的斜率
的斜率![]()
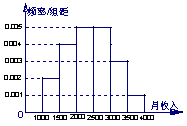
(16)一个社会调查机构就某地居民的月收入调查了10000人,并根据所得数据画了样本的频率分布直方图(如下图)![]() 为了分析居民的收入与年龄、学历、职业等方面的关系,要从这10000人中再用分层抽样方法抽出100人作进一步调查,则在
为了分析居民的收入与年龄、学历、职业等方面的关系,要从这10000人中再用分层抽样方法抽出100人作进一步调查,则在![]() (元)月收入段应抽出_____人
(元)月收入段应抽出_____人![]()
三.解答题:本大题共6小题,共74分![]() 解答应写出文字说明,证明过程或演算步骤
解答应写出文字说明,证明过程或演算步骤![]()
(17)(本小题满分12分)
在![]() ,求
,求
(1)![]()
(2)若点![]()
(18)(本小题满分12分)
设等比数列![]() 的前n项和为
的前n项和为![]() ,
,![]()
(19)(本小题满分12分)
某批产品成箱包装,每箱5件,一用户在购进该批产品前先取出3箱,再从每箱中任意出取2件产品进行检验![]() 设取出的第一、二、三箱中分别有0件、1件、2件二等品,其余为一等品
设取出的第一、二、三箱中分别有0件、1件、2件二等品,其余为一等品![]()
(I)求取6件产品中有1件产品是二等品的概率![]()
(II)若抽检的6件产品中有2件或2件以上二等品,用户就拒绝购买这批产品,求这批产品被用户拒绝的概率![]()
(20)(本小题12分)
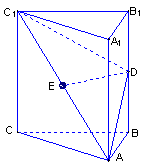
如图,在直三棱柱![]() 中,
中,![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点
的中点![]()
(I)证明:ED为异面直线![]() 与
与![]() 的公垂线;
的公垂线;
(II)设![]() 求二面角
求二面角![]() 的大小
的大小
(21)(本小题满分为14分)
设![]() ,函数
,函数![]() 若
若![]() 的解集为A,
的解集为A,![]() ,求实数
,求实数![]() 的取值范围
的取值范围![]()
(22)(本小题满分12分)
已知抛物线![]() 的焦点为F,A、B是抛物线上的两动点,且
的焦点为F,A、B是抛物线上的两动点,且![]() 过A、B两点分别作抛物线的切线,设其交点为M
过A、B两点分别作抛物线的切线,设其交点为M![]()
(I)证明![]() 为定值;
为定值;
(II)设![]() 的面积为S,写出
的面积为S,写出![]() 的表达式,并求S的最小值
的表达式,并求S的最小值![]()