高三4月模拟考试理科数学试卷
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,用时120分钟.
第Ⅰ卷(选择题,满分50分)
一、选择题(本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的,把正确的代号填在指定位置上)
1.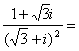 [ B ]
[ B ]
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.下列命题中,正确的个数是[ B ]
①若+=0,则==; ②在△ABC中,若++=,则O为△ABC的重心;
③若,是共线向量,则·=·,反之也成立;
④若,是非零向量,则+=的充要条件是存在非零向量,使·+·=0.
A.1 B.2 C.3 D.4
3.若命题P:x∈A∩B,则﹁P [ B ]
![]()
![]()
![]()
![]()
![]() A.x∈A且x∈B B.x∈A或x∈B C.x∈A且x∈B D.x∈A∪B
A.x∈A且x∈B B.x∈A或x∈B C.x∈A且x∈B D.x∈A∪B
4.已知函数f(x)=log2ax-1 (a≠0)满足关系式f(-2+x)=f(―2―x),则a的值为[ C ]
A.1 B. C.- D.-1
5.已知f(x)=2x+3,(x∈R),若f(x)-1<a的必要条件是x+1<b,(a、b>0).则a、b之间的关系是[ C ]
A.a≤ B.b< C.b≥ D.a>
6.已知![]() =[ A ]
=[ A ]
A.0 B.2 C.4 D.8
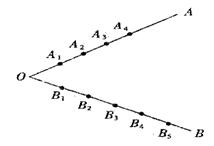 7.如图,在∠AOB的两边上分别为A1、A2、A3、A4和B1、B2、B3、B4、B5共9个点,连结线段AiBi(1≤i≤4,1≤j≤5),如果其中两条线段不相交,则称之为一对“和睦线”,则图中共有[ A ]对“和睦线” ( )
7.如图,在∠AOB的两边上分别为A1、A2、A3、A4和B1、B2、B3、B4、B5共9个点,连结线段AiBi(1≤i≤4,1≤j≤5),如果其中两条线段不相交,则称之为一对“和睦线”,则图中共有[ A ]对“和睦线” ( )
A.60
B.62
C.72
D.124
8.函数y=-sinx+cosx在x∈[-,]时的值域是[ C ]
A.[0, ] B.[-,0] C.[0, ] D.[0,1]
9.在圆周上有10个等分点,以这些点为顶点,每3个点可以构成一个三角形,如果随机选择了3个点,刚好构成直角三角形的概率是[ C ]
A. B. C. D.
10.已知椭圆![]() 的左、右焦点分别为F1、F2,且F1F2=2c,点A在椭圆上,
的左、右焦点分别为F1、F2,且F1F2=2c,点A在椭圆上,![]() =0
=0![]() ,则椭圆的离心率e=[ C ]
,则椭圆的离心率e=[ C ]
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
第Ⅱ卷(非选择题,共计100分)
二、填空题(本大题共5小题,每小题5分,共25分,把正确的答案填在指定位置上)
11.若数列x,a1,a2,y成等差数列,x,b1,b2,y成等比数列,则的取值范围是 (-∞,0)∪[4,+∞] .
12.将函数y=x2的图象F按向量=(3,-2)平移到F′,则F′的函数解析式为 y=x2-6x+7 .
13.设随机变量ξ服从正态分布N(1,22),若P(ξ≤c)=43P(ξ>c),则常数c= 5 (参考数据:φ(2)=0.9773)
14.在实数的原有运算法则中,我们补充定义新运算“+”如下:当a≥b时,a+b=a;当a<b时,a+b=b2;则函数f(x)=(1+x)·x―(2+x),x∈[―2,2]的最大值等于 6 (“·”与“-”分别为乘法与减法).
15.设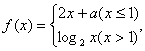 若
若![]() 存在,则常数
存在,则常数![]() __-2 .
__-2 .
三.解答题(本大题共6个小题,共75分).
16.(本小题满分12分)已知向量=(cos4x,-1),=(1,cin4x+sin2x),x∈R,f(x)=·.
(1)求函数f(x)的最小正周期; (2)若x∈[0, ],求f(x)的最值及相应的x值.
解:f(x)=·=cos4x―sin4x―sin2x=cos2x-sin2x=2cos(2x+).
(1)函数f(x)的最小正周期T=π.
(2).∵x∈[0, ]∴2x+∈[,].
∴当2x+=即x=0时,f(x)mox=1.
当2x+=π即x=时,f(x)min=-2.
17. (本小题满分12分)某校的一个研究性学习小组进行一种验证性实验,已知该种实验每次实验成功的概率为![]() .
.
(1)求他们做了5次这种实验至少有2次成功的概率;
(2)如果在若干次实验中累计有两次成功就停止实验,否则将继续进行下次实验,但实验的总次数最多不超过5次,求该小组做实验的次数![]() 的概率分布列和期望.
的概率分布列和期望.
解:(1)设5次实验中,只成功一次为事件A,一次都不成功为事件B,至少2次成功为事件C,则
P(C)=1-P(A+B)=1-P(A)-P(B)------------------2分
=1-![]() =
=![]()
所以5次实验至少2次成功的概率为![]() .---------------------5分
.---------------------5分
(2) ![]() 的可能取值为2,3,4,5.
的可能取值为2,3,4,5.
又∵![]() ;
;![]()
![]()
![]() -----------9分
-----------9分
(每对一个得1 分)
∴![]() 的分布列为:
的分布列为:
|
| 2 | 3 | 4 | 5 |
| P |
|
|
|
|
----------------------------10分
∴Eξ=![]() ×2+
×2+![]() ×3+
×3+![]() ×4+
×4+![]() ×5=
×5=![]() -------------------------12分
-------------------------12分
18.(本小题满分12分)平面内有向量=(1,7),=(5,1),=(2,1),点Q为直线OP上的一个动点.
(1)当·取最小值时,求的坐标;
(2)当点Q满足(1)的条件和结论时,求cos∠AQB的值.
解:设=(x.y),∵与共线![]() x=2y. ∴=(2y,y),又=-=(1―2y,7―y),
x=2y. ∴=(2y,y),又=-=(1―2y,7―y),
=-=(5―2y,1―y).
∴·=(1―2y)(5―2y)+(7―y)(1―y) =5y2-20y+12
 =5(y―2)2―8≥―8.此时y=2,=(4,2).
=5(y―2)2―8≥―8.此时y=2,=(4,2).
(2)当=(4,2)时,=(-3,5),=(1,-1),
·=-8.
∴cos∠AQB===-.
19.
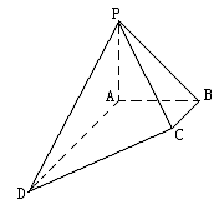
(本小题满分12分)如图,在四棱锥![]() 中,侧棱PA⊥底面ABCD, AD∥BC,∠ABC=
中,侧棱PA⊥底面ABCD, AD∥BC,∠ABC=![]() ,
,![]() ,
,![]() .
.
(Ⅰ) 求点D到平面PBC的距离; (Ⅱ) 求二面角![]() 的大小.
的大小.
|
解:(Ⅰ)如图,在四棱锥![]() 中,
中,
∵BC∥AD,从而点D到平面PBC间的距离等于点A到平面PBC的距离.
∵∠ABC=![]() ,∴AB⊥BC, 又PA⊥底面ABCD,∴PA⊥BC,
,∴AB⊥BC, 又PA⊥底面ABCD,∴PA⊥BC,
∴BC⊥平面 PAB,………………2分
∴平面PAB⊥平面PBC,交线为PB,过A作AE⊥PB,垂足为E,则AE⊥平面PBC,
∴AE的长等于点D到平面PBC的距离.而![]() ,∴
,∴![]() .………5分
.………5分
|
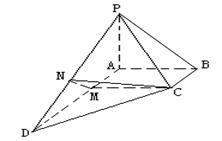
(Ⅱ) ∵PA⊥底面ABCD,∴平面PAD⊥底面ABCD,
引CM⊥AD于M,MN⊥PD于N,则CM⊥平面PAD,
∴MN是CN在平面PAD上的射影,
由三垂线定理可知CN⊥PD,
∴∠CNM是二面角![]() 的平面角.…………9分
的平面角.…………9分
依题意![]() ,
,![]() ,
,
∴![]() ,∴
,∴![]() ,
,
可知![]() ,∴
,∴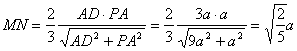 ,
,
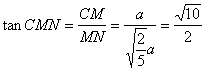 ,∴二面角
,∴二面角![]() 的大小为
的大小为![]() …… 12分
…… 12分
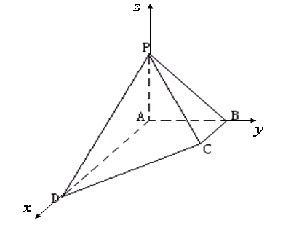
解法二:如图, A为原点,分别以AD、AB、AP为x轴、y轴、z轴建立空间直角坐标系.
|
∴![]() ,
,
∴![]() . 则
. 则![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
∴![]() ,
,![]() ,
,![]() .
.
设平面PBC的一个法向量为![]() ,则
,则
![]() 令
令![]() ,得
,得![]() ,
,
则点D到平面PBC的距离等于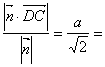
![]() .……………6分
.……………6分
(Ⅱ) ∵AB⊥PA,AB⊥AD,∴AB⊥底面PDA,∴平面PDA的一个法向量为![]() .
.
设平面PDC的一个法向量为![]() ,
,
∵![]() ,
,![]() ,∴
,∴![]()
令![]() ,得
,得![]() ,∴
,∴![]() .
.
∵二面角![]() 是锐二面角,∴二面角
是锐二面角,∴二面角![]() 的大小为
的大小为![]() .……12分
.……12分
20.(本小题满分13分)
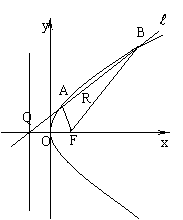
如图,![]() 是抛物线
是抛物线![]() 的焦点,
的焦点,![]() 是准线与
是准线与![]() 轴的交点,直线
轴的交点,直线![]() 经过点
经过点![]() 。
。
(1)
直线![]() 与抛物线有唯一公共点,求
与抛物线有唯一公共点,求![]() 的方程;
的方程;
(2)
直线![]() 与抛物线交于A,B两点,
与抛物线交于A,B两点,
(Ⅰ)记![]() 的斜率分别为
的斜率分别为![]() ,求
,求![]() 的值;
的值;
(Ⅱ)若点![]() 在线段
在线段![]() 上,且满足
上,且满足![]() ,求点
,求点![]() 的轨迹方程。
的轨迹方程。
解: 依题意![]() ,直线
,直线![]() 斜率存在,设其斜率为
斜率存在,设其斜率为![]() ,则
,则![]() 的方程为
的方程为![]() ,代入抛物线方程有:
,代入抛物线方程有:![]() ……………2分
……………2分
(1)若![]() ,令
,令![]() 得,
得,![]() ,此时,
,此时,![]() 的方程为
的方程为![]() 。…………………4分
。…………………4分
若![]() ,方程有唯一解。此时方程为
,方程有唯一解。此时方程为![]() ………5分
………5分
(2)显然![]() ,记
,记![]() ,
,
则![]() ,
,![]() ,
,![]() ………7分
………7分
(Ⅰ)![]() ………………………9分
………………………9分
(Ⅱ)设点![]() 的坐标为
的坐标为![]() ,∵
,∵![]() ,∴
,∴![]() ,
,
∴![]() …………………11分 ∴
…………………11分 ∴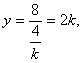
![]() ,………12分
,………12分
由![]() 得,
得,![]() ,又
,又![]() ,∴
,∴![]() 。
。
综上,点R的轨迹方程为![]()
![]() 。…………………………13分
。…………………………13分
21.(本小题满分14分)已知函数![]()
(1) 若![]() 在
在![]() 上单调递增,求
上单调递增,求![]() 的取值范围;
的取值范围;
(2) 若定义在区间D上的函数![]() 对于区间D上的任意两个值
对于区间D上的任意两个值![]() 总有以下不等式
总有以下不等式![]() 成立,则称函数
成立,则称函数![]() 为区间D上的“凹函数”.
为区间D上的“凹函数”.
试判断当![]() 时,
时,![]() 是否为“凹函数”,并对你的判断加以证明.
是否为“凹函数”,并对你的判断加以证明.
解:(Ⅰ)由![]() ,得
,得![]() ……………………2分
……………………2分
欲使函数为![]() 上单调增函数,则
上单调增函数,则![]() 在
在![]() 上恒成立,即不等式
上恒成立,即不等式![]() 在
在![]() 上恒成立.也即
上恒成立.也即![]() 在
在![]() 上恒成立.………………4分
上恒成立.………………4分
令![]() ,上述问题等价于
,上述问题等价于![]() ,而
,而![]() 为在
为在![]() 上的减函数,则
上的减函数,则![]() ,于是
,于是![]() 为所求. ………………………………………………6分
为所求. ………………………………………………6分
(Ⅱ)证明:由![]() 得
得
![]()
![]() ………………………………7分
………………………………7分
![]() ………………………………………8分
………………………………………8分
而![]() ① ………………………10分
① ………………………10分
又![]() , ∴
, ∴![]() ② …………11分
② …………11分
∵![]() ∴
∴![]() ,
,
∵![]() ∴
∴![]() ③ …………………………………13分
③ …………………………………13分
由①、②、③得![]()
即![]() ,
,
从而由凹函数的定义可知函数为凹函数. …………14分
湖南省部分中学2007年4月高三调研联考数学理科
本试题分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。共150分。考试时间120分钟。
第Ⅰ卷(选择题,共50分)
一、选择题:(本大题共10小题,每小题5分,共50分,)
1.复数Z=![]() 为纯虚数,则实数m= ( )
为纯虚数,则实数m= ( )
A.-1.or.3 B.![]() C.3 D.1
C.3 D.1
2.已知等差数列{![]() 中,
中,![]() ,则
,则![]() ( )
( )
A.20 B.22 C.26 D.28
3.设函数![]() ,对于任意实数
,对于任意实数![]() ,且方程
,且方程![]() =0有2007个解,则这2007个解之和为( )
=0有2007个解,则这2007个解之和为( )
A.0 B.-1 C.2007 D.4014。
4.对于直线m.n和平面α,下面命题中的真命题是( )
![]()
![]()
![]()
![]()
5.若![]() 是函数y=f(x)=
是函数y=f(x)=![]() 的反函数,若
的反函数,若![]() ,则
,则![]()
A 1.
B.
2
C.
3
D.
![]()
6、在![]() 的展开式中,第五项的系数与第七项的系数相等,则n=( )
的展开式中,第五项的系数与第七项的系数相等,则n=( )
A.8 B.9 C.10 D.11
7.有7个高矮不一的同学排成一排,最高的站在中间,两边各有3名同学,使得最高的同学的两边越往边上越矮,则不同的排队方式共有( )
A. ![]() B.
B.![]() C.
C.![]() D.
D.![]()
8、在平面四边形ABCD中,P为平面上一点,若![]() ,则点P为( )
,则点P为( )
A.四边形ABCD对角线的交点 B.AC的中点 C.BD的中点 D.在CD边上。
9.已知椭圆![]() 的左、右焦点为
的左、右焦点为![]() ,P为椭圆上的一点,且
,P为椭圆上的一点,且![]() 的最大值的取值范围是
的最大值的取值范围是![]() 。则椭圆的离心率的范围为 ( )
。则椭圆的离心率的范围为 ( )
A. ![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.已知函数![]() ,在
,在![]() 时取最小值,则函数
时取最小值,则函数![]() 是( )
是( )
A.偶函数且图像关于点![]() 对称, B.偶函数且图像关于点
对称, B.偶函数且图像关于点![]() 对称,
对称,
C.奇函数且图像关于点![]() 对称, D.奇函数且图像关于点
对称, D.奇函数且图像关于点![]() 对称,
对称,
第Ⅱ卷(非选择题 共100分)
二、填空题:(本大题共5 小题,每小题4 分,共20 分,把答案填在横线上。)
11.已知实数x、y满足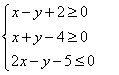 ,则
,则![]() 的最大值为_______
的最大值为_______
12. 如图,在正三棱柱ABC-![]() 中,AB=1,点D在棱
中,AB=1,点D在棱![]() 上,BD=1,若AD与平面B
上,BD=1,若AD与平面B![]() C所成的角为a,则sina=________.
C所成的角为a,则sina=________.
13.直线L是过y=![]() 图像上的定点P(1,-1)的切线,点P关于直线y=x的对称点为C,则以C为圆心,且与直线L相切的圆的标准方程是_________.
图像上的定点P(1,-1)的切线,点P关于直线y=x的对称点为C,则以C为圆心,且与直线L相切的圆的标准方程是_________.
14.在实数集R上定义运算![]() 对任意实数x均成立,则实数
对任意实数x均成立,则实数![]() 的取值范围__________.
的取值范围__________.
15.下列命题中正确的序号是______________
①若命题P和命题Q中只有一个是真命题,则![]() P或Q是假命题
P或Q是假命题
②![]() 成立的必要不充分条件;
成立的必要不充分条件;
③若函数y=f(x)满足![]() 是周期函数;
是周期函数;
④若![]() ,则r的取值范围是
,则r的取值范围是![]() 。
。
三、解答题:(本大题共6 小题,共80 分,解答应写出文字说明,证明过程或演算步骤。)
16.(12分)在三角形ABC中,![]()
![]() 求A的大小;
求A的大小;![]() .。
.。
17.(本题满分12分)如图,四棱锥P-![]() CD中,PD⊥平面
CD中,PD⊥平面![]() ,PA与平面
,PA与平面![]() 所成的角为600,在四边形
所成的角为600,在四边形![]() 中,∠ADC=∠DAB=900,AB=4,CD=1,AD=2
中,∠ADC=∠DAB=900,AB=4,CD=1,AD=2
![]() 求异面直线PA与BC所成的角;
求异面直线PA与BC所成的角;
![]() 设
设![]() 。
。
18.(12分)甲、乙两人进行摸球游戏,一袋中装有2个黑球和1个红球。规则如下:若一方摸中红球,将此球放入袋中,此人继续摸球;若一方没有摸到红球,将摸到的球放入袋中,则由对方摸彩球。现甲进行第一次摸球。
![]() 设
设![]() 是前三次摸球中,甲摸到的红球的次数,求随机变量
是前三次摸球中,甲摸到的红球的次数,求随机变量![]() 的概率分布与期望。
的概率分布与期望。
![]() 在前四次摸球中,甲恰好摸中两次红球的概率。
在前四次摸球中,甲恰好摸中两次红球的概率。
19.(12分)有一个受到污染的湖泊,其湖水的容积为V立方米,每天流入流出湖泊的水量都是r立方米,现假设下雨与蒸发正好平衡,且污染物质与湖水能很好地混合,用g(t)表示第t天每立方米湖水所含污染物质的克数,我们称g(t)为第t天的湖水污染质量分数,已知目前每天流入湖泊的水中有p克的污染物质污染湖水,湖水污染物质分数满足关系式:![]() 。
。
![]() 当湖水污染质量分数为常数时,求湖水污染的初始质量分数;
当湖水污染质量分数为常数时,求湖水污染的初始质量分数;
![]() 求证:当
求证:当![]() 时,湖泊的污染程度越来越严重。
时,湖泊的污染程度越来越严重。
(3)如果政府加大治污力度,使得流入湖泊的所有污染停止,那么需要经过多少天才能使湖水的污染水平下降到开始时的污染水平的5%?
20.(本题满分13分)
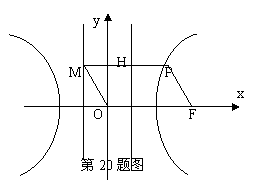 如图,F为双曲线C:
如图,F为双曲线C:![]() 的右焦点。P为双曲线C右支上一点,且位于
的右焦点。P为双曲线C右支上一点,且位于![]() 轴上方,M为左准线上一点,
轴上方,M为左准线上一点,![]() 为坐标原点。已知四边形
为坐标原点。已知四边形![]() 为平行四边形,
为平行四边形,![]() 。
。
(Ⅰ)写出双曲线C的离心率![]() 与
与![]() 的关系式;
的关系式;
(Ⅱ)当![]() 时,经过焦点F且品行于OP的直线交双曲线于A、B点,若
时,经过焦点F且品行于OP的直线交双曲线于A、B点,若![]() ,求此时的双曲线方程。
,求此时的双曲线方程。
21.(14分)设函数![]() 的定义域与值域均为R,
的定义域与值域均为R,![]() 的反函数为
的反函数为![]() ,定义数列{
,定义数列{![]() 中,
中,![]() ,……。
,……。
![]() 若对于任意实数x,均有
若对于任意实数x,均有![]() +
+![]() =2.5x,求证:①
=2.5x,求证:①![]() ,……。
,……。
②设![]() ……,求{
……,求{![]() 的通项公式。
的通项公式。
![]() 若对于任意实数x,均有
若对于任意实数x,均有![]() +
+![]() <2.5x,是否存在常数A、B同时满足:
<2.5x,是否存在常数A、B同时满足:
①当n=0.or.n=1时,有![]() 成立;②当n=2、3、4、……,时,
成立;②当n=2、3、4、……,时,![]() 成立。
成立。
如果存在,求出A、B的值;如果不存在,说明理由。
参考答案
一、选择题
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| C | D | C | C | B | B | D | B | A | D |
二、填空题:![]()
![]()
![]()
![]()
![]()
![]() ②③④
②③④
三、解答题:(本大题共6 小题,共80 分,解答应写出文字说明,证明过程或演算步骤。)
16.(12分)在三角形ABC中,![]()
![]() 求A的大小;
求A的大小;![]() .。
.。
解![]() 。
。
17.(本题满分12分)如图,四棱锥P-![]() CD中,PD⊥平面
CD中,PD⊥平面![]() ,PA与平面
,PA与平面![]() 所成的角为600,在四边形
所成的角为600,在四边形![]() 中,∠ADC=∠DAB=900,AB=4,CD=1,AD=2
中,∠ADC=∠DAB=900,AB=4,CD=1,AD=2
![]() 求异面直线PA与BC所成的角;
求异面直线PA与BC所成的角;
![]() 设
设![]() 。
。
解: ![]() 建立坐标系,
建立坐标系,![]() 易求异面直线PA与BC所成的角为
易求异面直线PA与BC所成的角为![]() ;
;
![]()
![]()
18.(12分)甲、乙两人进行摸球游戏,一袋中装有2个黑球和1个红球。规则如下:若一方摸中红球,将此球放入袋中,此人继续摸球;若一方没有摸到红球,将摸到的球放入袋中,则由对方摸彩球。现甲进行第一次摸球。
![]() 设
设![]() 是前三次摸球中,甲摸到的红球的次数,求随机变量
是前三次摸球中,甲摸到的红球的次数,求随机变量![]() 的概率分布与期望。
的概率分布与期望。
![]() 在前四次摸球中,甲恰好摸中两次红球的概率。
在前四次摸球中,甲恰好摸中两次红球的概率。
解: 18、(1)![]() 的分布是
的分布是
|
| 0 | 1 | 2 | 3 |
| P |
|
|
|
|
E![]() =
=![]()
(2) ![]()
19.(12分)有一个受到污染的湖泊,其湖水的容积为V立方米,每天流入流出湖泊的水量都是r立方米,现假设下雨与蒸发正好平衡,且污染物质与湖水能很好地混合,用g(t)表示第t天每立方米湖水所含污染物质的克数,我们称g(t)为第t天的湖水污染质量分数,已知目前每天流入湖泊的水中有p克的污染物质污染湖水,湖水污染物质分数满足关系式:![]() 。
。
![]() 当湖水污染质量分数为常数时,求湖水污染的初始质量分数;
当湖水污染质量分数为常数时,求湖水污染的初始质量分数;
![]() 求证:当
求证:当![]() 时,湖泊的污染程度越来越严重。
时,湖泊的污染程度越来越严重。
(3)如果政府加大治污力度,使得流入湖泊的所有污染停止,那么需要经过多少天才能使湖水的污染水平下降到开始时的污染水平的5%?
解:![]()
(1) ![]()
(2)由![]() 知
知![]() ,所以g(t)为增函数,湖泊的污染程度越来越严重。
,所以g(t)为增函数,湖泊的污染程度越来越严重。
(3)由p=0及![]()
所以需要经过![]() 天才能使湖水的污染水平下降到开始时的污染水平的5%。
天才能使湖水的污染水平下降到开始时的污染水平的5%。
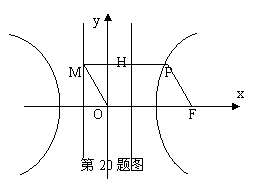
20.(本题满分13分)
如图,F为双曲线C:![]() 的右焦点。P为双曲线C右支上一点,且位于
的右焦点。P为双曲线C右支上一点,且位于![]() 轴上方,M为左准线上一点,
轴上方,M为左准线上一点,![]() 为坐标原点。已知四边形
为坐标原点。已知四边形![]() 为平行四边形,
为平行四边形,![]() 。
。
(Ⅰ)写出双曲线C的离心率![]() 与
与![]() 的关系式;
的关系式;
(Ⅱ)当![]() 时,经过焦点F且品行于OP的直线交双曲线于A、B点,若
时,经过焦点F且品行于OP的直线交双曲线于A、B点,若![]() ,求此时的双曲线方程。
,求此时的双曲线方程。
解:∵四边形![]() 是
是![]() ,∴
,∴![]() ,作双曲线的右准线交PM于H,则
,作双曲线的右准线交PM于H,则![]() ,又
,又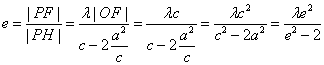 ,
,![]() 。
。
(Ⅱ)当![]() 时,
时,![]() ,
,![]() ,
,![]() ,设双曲线为
,设双曲线为![]()
又四边形![]() 是菱形,所以直线OP的斜率为
是菱形,所以直线OP的斜率为![]() ,则直线AB的方程为
,则直线AB的方程为![]() ,代入到双曲线方程得:
,代入到双曲线方程得:![]() ,
,
又![]() ,由
,由![]() 得:
得:![]() ,则
,则![]() ,所以
,所以![]() 为所求。
为所求。
21.(14分)设函数![]() 的定义域与值域均为R,
的定义域与值域均为R,![]() 的反函数为
的反函数为![]() ,定义数列{
,定义数列{![]() 中,
中,![]() ,……。
,……。
![]() 若对于任意实数x,均有
若对于任意实数x,均有![]() +
+![]() =2.5x,求证:①
=2.5x,求证:①![]() ,……。
,……。
②设![]() ……,求{
……,求{![]() 的通项公式。
的通项公式。
![]() 若对于任意实数x,均有
若对于任意实数x,均有![]() +
+![]() <2.5x,是否存在常数A、B同时满足:
<2.5x,是否存在常数A、B同时满足:
①当n=0.or.n=1时,有![]() 成立;②当n=2、3、4、……,时,
成立;②当n=2、3、4、……,时,![]() 成立。
成立。
如果存在,求出A、B的值;如果不存在,说明理由。
解:(1)由![]() ,又在等式
,又在等式![]() +
+![]() =2.5x中令
=2.5x中令![]() ,
,
从而有![]() ………………(1)成立。
………………(1)成立。
又![]() 及(1)式有:
及(1)式有:![]() ,所以{
,所以{![]()
![]() ,
,
![]() 。
。
(2)由n=0.or.n=1时,有![]() 成立,可求得A=B=4,
成立,可求得A=B=4,
由对于任意实数x,均有![]() +
+![]() <2.5x,可得
<2.5x,可得![]() ………………(2)
………………(2)
下面利用(2)和A=B=4,用数学归纳法证明:
当n=2、3、4、……,时,![]() 成立即可,证明过程容易,略去。
成立即可,证明过程容易,略去。
所以存在实数A=B=4,使结论成立。