高三自测数学试题
一、选择题(本大题共12小题,每小题5分,计60分.)
1.设全集![]() ,
,![]() ,
,![]() ,那么
,那么![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.函数![]() 的反函数是 (
)
的反函数是 (
)
A.![]() B.
B.![]()
C.![]() D.
D.![]()
3.数列![]() 中,
中,![]() ,且
,且![]() ,则数列
,则数列![]() 的前8项和等于
( )
的前8项和等于
( )
A.2
B.![]() D.
D.![]()
4.将一张坐标纸折叠,使得点(0,2)与点(![]() ,0)重合,且点(2005,2006)与点(
,0)重合,且点(2005,2006)与点(![]() )重合,则
)重合,则![]() 的值为 ( )
的值为 ( )
A.1 B.![]() C.0 D.2007
C.0 D.2007
5.已知![]() ,
,![]() 与
与![]() 的夹角为60°,
的夹角为60°,![]() ,
,![]() ,则
,则![]() 的值为 ( )
的值为 ( )
A.![]() B.
B.![]() C.1 D.2
C.1 D.2
6.定义在R上的奇函数![]() 是周期函数,T为其一个周期,则
是周期函数,T为其一个周期,则![]() 的值是
( )
的值是
( )
A.T
B.![]() C.0 D.无法确定
C.0 D.无法确定
7.在△ABC中,A=![]() ,BC=3,则△ABC的周长为 (
)
,BC=3,则△ABC的周长为 (
)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.设![]() 为两条直线,
为两条直线,![]() 为两个平面,给出下列四个命题,其中正确命题的个数为 ( )
为两个平面,给出下列四个命题,其中正确命题的个数为 ( )
(1)若![]()
![]() ∥
∥![]() ,
,![]() ∥
∥![]() ,则
,则![]() ∥
∥![]() (2)若
(2)若![]() ,则
,则![]() ∥
∥![]()
(3)若![]() ∥
∥![]() ,
,![]() ∥
∥![]() ,则
,则![]() ∥
∥![]() (4)若
(4)若![]() ,则
,则![]()
A.0个 B.1个 C.2个 D.3个
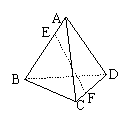
9.如图,正四面体ABCD中,E在棱AB上,F在棱CD上,使![]() ,设
,设![]() ,
,![]() 表示EF与AC所成的角,
表示EF与AC所成的角,![]() 表示EF与BD所成的角,则 ( )
表示EF与BD所成的角,则 ( )
 A.
A.![]() 在(0,+∞)上单调增加
在(0,+∞)上单调增加
B.![]() 在(0,+∞)上单调减少
在(0,+∞)上单调减少
C.![]() 在(0,1)上单调增加,而在(1,+∞)上单调减少
在(0,1)上单调增加,而在(1,+∞)上单调减少
D.![]() 在(0,+∞)上为常数
在(0,+∞)上为常数
10.已知抛物线![]() ,过焦点的弦AB被焦点分成长为
,过焦点的弦AB被焦点分成长为![]() 的两段,那么( )A.
的两段,那么( )A.![]() B.
B.![]() ·
·![]() C.
C.![]() D.
D.![]()
11.正方体ABCD-A1B![]() ,点P是平面ABCD上的一个动点,且动点P到直线A1D1的距离与动点P到点M的距离的平方差是1,则动点P的轨迹是
(
)
,点P是平面ABCD上的一个动点,且动点P到直线A1D1的距离与动点P到点M的距离的平方差是1,则动点P的轨迹是
(
)
A.直线 B.圆 C.双曲线 D.抛物线
12.设A、B是椭圆![]() 上的两个动点,一个焦点是F,则△ABF的周长的最大值为 (
)
上的两个动点,一个焦点是F,则△ABF的周长的最大值为 (
)
A.6 B.
二、填空题(本大题共6小题,每小题4分,计24分)
13.命题“若![]() ,则
,则![]() 全为
全为
14.如果函数![]() 在区间(
在区间(![]() )上是减函数,那么实数
)上是减函数,那么实数![]() 的取值范围是
.
的取值范围是
.
15.已知![]() 满足约束条件
满足约束条件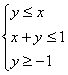 ,则
,则![]() 的最大值是
.
的最大值是
.
16.若已知椭圆![]() 的一条准线与抛物线
的一条准线与抛物线![]() 的准线重合,则
的准线重合,则
![]() .
.
17.如图设平面![]() ,
,![]() ,垂足分别为B、D,若增加一个条件就
,垂足分别为B、D,若增加一个条件就
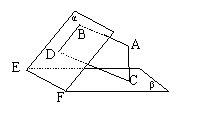 能推出BD⊥EF,现有
能推出BD⊥EF,现有
①AC⊥![]() ;
;
②AC与![]() 所成的角相等;
所成的角相等;
③AC与CD在![]() 内的射影在同一条直线上;
内的射影在同一条直线上;
④AC∥EF,那么上述几个条件中能成为增加条件的是 .
18.已知平面上点![]() ,则满足条件的点P在平面上所组成图形的面积是
.
,则满足条件的点P在平面上所组成图形的面积是
.
数学试题答题纸
一、选择题答题表:
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
二、填空题答案:
13. 14.
15. 16.
17. 18.
三、解答题(本大题共5小题,计66分)
19.(本题满分12分)已知A、B、C三点的坐标分别是A(3,0),B(0,3),C(![]() ),其中
),其中![]() .
.
(1)若![]() ,求角
,求角![]() 的值;
的值;
(2)若![]() ·
·![]() ,求
,求![]() 的值.
的值.
。
20. (本题满分12分)已知函数![]() ,数列
,数列![]() 是公差为
是公差为![]() 的等差数列,
的等差数列,![]() 是公比为
是公比为![]() 的等比数列,设
的等比数列,设![]()
![]() ;
;
(1)求数列![]() 和
和![]() 的通项公式;
的通项公式;
(2)设数列![]() 对一切正整数n,都有
对一切正整数n,都有![]() =
=![]() 成立,求数列
成立,求数列![]() 的前n项和
的前n项和![]() .
.
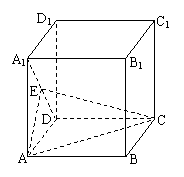 21. (本题满分14分)如图,已知棱长为
21. (本题满分14分)如图,已知棱长为![]() 的正方体ABCD-A1B
的正方体ABCD-A1B
(1)求证:AE⊥平面CDE;
(2)求二面角E-AC-D的正切值;
(3)求点B到平面ACE的距离.
22.(本题满分14分)已知![]()
(1)若![]() ,求
,求![]() 的单调区间;
的单调区间;
(2)若![]() ,且当
,且当![]() 时恒有
时恒有![]() ,求
,求![]() 的取值范围.
的取值范围.
23.(本题满分14分)如图,直角坐标系![]() 中,一直角三角形ABC,∠C=90°,B、C在
中,一直角三角形ABC,∠C=90°,B、C在![]() 轴上,且关于原点O对称,D在边BC上,BD=3DC,△ABC的周长为12,若一双曲线E以B、C为焦点,且经过A、D两点.
轴上,且关于原点O对称,D在边BC上,BD=3DC,△ABC的周长为12,若一双曲线E以B、C为焦点,且经过A、D两点.
(1)求双曲线E的方程;
 (2)若一过点P(m,0)(m为常数,且m≠0)的直线
(2)若一过点P(m,0)(m为常数,且m≠0)的直线![]() 与双曲线E相交于不同于双曲线顶点的两点M、N,且
与双曲线E相交于不同于双曲线顶点的两点M、N,且![]() ,问在
,问在![]() 轴上是否存在定点G,使
轴上是否存在定点G,使![]() ?若存在,求出所有这样定点G的坐标,若不存在,请说明理由.
?若存在,求出所有这样定点G的坐标,若不存在,请说明理由.