高三数学第二轮复习教学案
第四课时 函数的性质
班级______学号______姓名______
【考纲解读】1.理解函数的概念，会求函数的定义域、值域、解析式；
2.理解函数的奇偶性、单调性、周期性、对称性，能综合运用性质解决函数问题
【教学目标】1.正确理解、运用函数的概念；
2.掌握求函数的定义域、值域、解析式的基本方法；
3.能正确判断函数的奇偶性、单调性、周期性、对称性，并利用函数性质解决相关问题
【例题讲解】
例1 (1).函数
的定义域为
( )
A．（1，2）∪（2，3） B．
C．（1，3） D．[1，3]
(2).下列函数既是奇函数，又在区间
上单调递减的是 （ ）
A.
B.
C.
D.
(3).函数
的值域是
( )
A.(
) B.
C.
D.
(4).若函数
在区间
内恒有
>0，则的单调递增区间为
( )
A．
B．
C．(0,¥) D．
(5).函数
在[0，1]上的最大值与最小值之和为a，则a的值为
.
(6).设定义在
上的函数
满足
且当
时,
则在
上的表达式
.
例2.设函数
，且
（1）
求的解析式及定义域；（2）求的值域；（3）讨论的单调性
例3.设函数
（1）求的定义域；（2）判断的奇偶性；
（3）求证在区间
上单调递增
例4.已知二次函数的二次项系数为
，且不等式
的解集为（1，3）.
（1）如果方程
有两个相等的根，求的解析式；
（2）如果函数的最大值为正数，求的取值范围.
例5.已知函数
.
（1）求函数的定义域、值域；
（2）是否存在实数
，使得函数满足：对于区间
上使函数有意义的一切
，都有
高三数学第二轮复习教学案
第五课时 函数的图象
班级______学号______姓名______
【考纲解读】1.掌握作图象的基本方法，能够利用函数的性质描绘函数图象；熟练作出基本初等函数的图象；
2.掌握函数图象的平移变换、对称变换、伸缩变换及简单应用，以达到识图、作图和用图的目的；
3.了解函数图象与反函数图象间的对称关系及其应用.
【教学目标】1.能熟练地根据函数的性质作出函数的图象，并判断函数的对称轴等基本特征；
2.培养学生数形结合思想，能知图选式、知式选图、图象变换.
【例题讲解】
例1. (1)函数
图象过两点(-1,0)和(0,1),则
（ ）
(2).已知函数
满足
且
时，
，则函数的图象与
的图象的交点个数为
（ ）
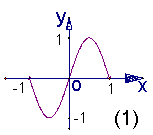
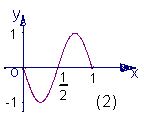
(3).已知函数
的图象的一部分如图⑴，则图⑵的函数图象所对应的函数解析式可以为
（ ）
(4).函数
满足
则
______. 
若函数
的图象关于直线
对称,则
的值是________________.
(6).若函数的图象关于点
对称,且存在反函数
,若
,则于
______.
例2.已知函数与
的图象关于直线对称,求函数
的单调递减区间．
例3.设
函数
的图象关于原点对称.
(1)求的值;(2)求的反函数及反函数的定义域;
(3)对于给定的正实数
，解不等式
例4.已知函数的图象与函数
的图象关于点
对称.
(1)
求的表达式;
(2)若
且
在区间(0,2)上为减函数,求实数的取值范围.
例5.已知函数是函数
的反函数，函数的图象与函数
的图象关于直线
成轴对称图形，记
(1)求函数
的解析式及定义域；
(2)试问在函数的图象上是否存在两个不同的点
，使直线
恰好与
轴垂直.若存在，求出两点的坐标；若不存在，说明理由.
高三数学第二轮复习教学案
第六课时 抽象函数的性质研究
班级______学号______姓名______
【教学目标】理解抽象函数的意义，能根据函数方程等条件研究抽象函数的性质以及解决相关的综合问题．
【例题讲解】
例1.(1)若函数是定义在上的偶函数，在
上是减函数，且
则使得
的的取值范围是
( ) A. (-¥,2) B. (2,+¥) C. (-¥,-2)È(2,+¥) D.(-2,2)
(2). 设函数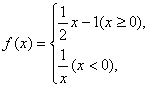
若
，则实数的取值范围是__________．
(3).函数对一切实数
均有
成立,且
则
．
(4).设函数在
内有定义，下列函数：①
②
③
④
中必是奇函数的是_______________（要求填写正确答案的序号）．
（5）.若函数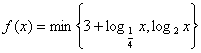
，其中
表示
两者中的较小者，
则
的解为 ．
(6).是定义在上的奇函数，且的图象关于直线
对称，则
________________.
例2.已知是定义在
上的偶函数，且在
上为增函数，若
，试求的取值范围．
例
．设是定义在上的偶函数，其图象关于直线
对称，若
时，
且
(1)求
、
；(2)求的周期．
例4.定义在上的单调函数满足
且对任意
都有
．
(1) 求证为奇函数；
(2) 若
对任意
恒成立，求实数的取值范围．
例5.函数
对于任意实数
,都有
.当
时,
且
.(1)求证
;(2)判断在
上的单调性;(3)若
,求正实数的值.