高三年级数学（文）一诊模拟考试
本试题分为第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分.共150分，考试时间150分钟.
第Ⅰ卷（选择题，共60分）
一、选择题（本大是共12小题，每小题5分，共60分。在小题中给出的四个选项中，只有一项是最符合题目要求的。）
1．tan675°的值为 （ ）
A．1 B．－1 C．
D．－
2．已知A={xx+1≥0}，B={yy2－4>0}，全集I=R，则A∩（C1B）为 （ ）
A．{xx≥2或x≤－2} B．{xx≥－1或x≤2}
C．{ x－1≤x≤2 } D．{ x－2≤x≤－1 }
3．过点（2，－2）且与双曲线
有相同渐近线的双曲线方程是 （ ）
A．
B．
C．
D．
4．已知等差数列{an}的公差为2，若a1，a3，a4成等比数列，则a2等于 （ ）
A．－4 B．－6 C．－8 D．－10
5．已知a、b、c满足c<b<a，且ac<0，那么下列选项中一定成立的是 （ ）
A．ab>ac B．c(b－a)<0 C．cb2<ab2 D．ac(a－c)>0
6．函数
的定义域是 （ ）
A．（－∞，4） B．[3，4
C．（3，4） D．[3，4]
7．向量
、
满足（－）·（2+）=－4，且=2，=4，则与夹角的余弦值等
于 （ ）
A．－
B． C．－
D．
8．在△ABC中，角A、B、C的对边分别是a、b、c，且∠A=2∠B，则
等于（ ）
A．
B．
C．
D．
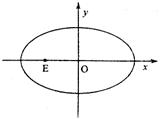
9．若O（0，0），A（4，－1）两点到直线ax+a2y+6=0的距离相等，则实数a可能取值的个
数共有（ ）个 （ ）
A．无数 B．2 C．3 D．4
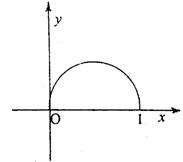
10．已知函数f(x)(0≤x≤1)的图象是一段圆弧（如图所示），若0<x1<x2<1，则 （ ）
|
B．
C．
D．前三个判断都不正确
11．已知
的最大值是 （ ）
A．2 B．－2 C．1 D．－1
12．在下列电路图中，表示开关A闭合是灯泡B亮的必要但不充分条件的线路图是（ ）
|
第Ⅱ卷（非选择题，共90分）
二、填空题（本大题共4个小题，每小题4分，共16分）
13．抛物线x2=y的准线方程为 。
14．数列{an}满足a1+a2+…+an=2n；则
= .
15．设有两个命题：①关于x的不等式mx2+1>0的解集是R，②函数f(x)=logmx是减函数.如果这两个命题中有且只有一个真命题，则实数m的取值范围是 .
16．设函数f(x)的图像与直线x=a，x=b及x轴所围成图形的面积称为函数f(x)在[a,b]上的面积。已知函数
，则函数
上的面积为
.
三、解答题（本大题共6小题，共74分，解答应写出文字说明，证明过程或演算步骤）
17．（本题满分12分）解关于x的不等式
.
18．（本题满分12分）设向量
，其中
.
| |
的取值范围；
（Ⅱ）若函数
的大小.
19．（本题满分12分）
某城市自来水厂蓄水池现有水9千吨，水厂每小时向池中注水2千吨，同时向全市供水，x小时内供水总量为
千吨，问：
（1）多少小时后，蓄水池内水量最少？
（2）当蓄水池水量少于3千吨时，供水会出现紧张现象，现决定扩大生产，每小时向池内注水3千吨，能否消除供水紧张现象，为什么？
20．（本题满分12分）已知函数
（1）当a=2时，求函数f(x)的最大值；
（2）函数f(x)的值域恰为
，试求出所有满足条件的自然数a所构成的集合.
21．（本题满分13分）
已知方向向量v= (1, 
)的直线l过点（0，－2）和椭圆C：
（a>b>0）的焦点，且椭圆C的中心关于直线l的对称点在椭圆C的右准线上。
（1）求椭圆C的方程；
|
（O为原点.）求直线m的方程.
22．（本小题满分12分）
已知f (x)是定义在R上的不恒为零的函数，且对于任意的a、b∈R都满足
（1）求
的值；
（2）判断f (x)的奇偶性，并证明你的结论；
（3）若
表示数列{bn}的前n项和.试问：是否存在关于n的整式g
(n)，使得S1+S2+S3+…+Sn－1 =（Sn－1）·g (n)对于一切不小于2的自然数n恒成立？若存在，写出g(n)的解析式，并加以证明；若不存在，试说明理由.
| |
参考答案
一、选择题
1.B 2.C 3.D 4.B 5.A 6.B 7.A 8.A 9.C 10.C
11.A 12.B
8．解：
∴选A.
9．由题意可知直线ax+a2y+6=0与直线OA平行或过O、A中点，
（1）当平行时
|
或a=－2 ∴选C.
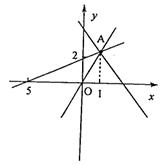
11．解：如图x+y－2=t过点A（1，2）时t取最大
∴（2x+y－2）max=2 ∴选A
二、填空题
13．
14．
15．
16．
16．解：由已知得正、余弦半个周期图象所围面积为
.
则y=cos3x半周期为
且
∴其所围面积为2×
三、解答题
17．解：（1）当x<－2或x>2且x≠3时不等式成立 4分
（2）－2<x<2时，4－x2>0，3－x>0；则原不等式等价于3－x≤4－x2 7分
解得
10分
综上所述：原不等式解集为{xx<－2 或或x>2且x≠3}
12分
18．解：（I）
2分
（II）
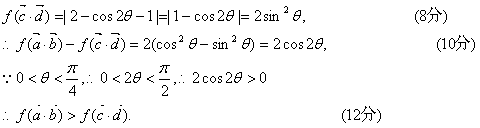
19．设x小时后，蓄水池有水y千吨，
（1）
3分
当x=4时，y最小=1
即4小时后，水量最少； 6分
（2）
9分
即扩大生产后，蓄水池水量最少是
千吨，可以消除供水紧张现象。 12分
20．解：（1）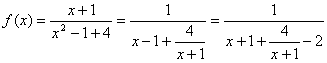
2分
时等号成立 4分
即当x=1∈[0，2]时f(x)的最大值为 6分
（2）假设存在这样的自然数a满足条件，
由（1）知当x=1时，ymax=则1∈[0，a]；所以a≥1 8分
又f(x)在[0，1]上单增，在[1，a] 上单减；且f(0)= 
所以只需
11分
解得0≤a≤3
又a≥1且a为自然数，所以a构成的集合为{1，2，3}. 13分
21．（1）直线
………………①过原点垂直l的直线方程为
……②
解①②得
.
∵椭圆中心（0，0）关于直线l的对称点在椭圆C的右准线上，
.
∵直线l过椭圆焦点，
∴该焦点坐标为（2，0）.
∴c=2,a2=6，b2=2. 故椭圆C的方程为
. ③ （5分）
（2）设M（x1，y1）N（x2，y2）.
设直线m：x=ty－2，代入③，整理得（t2+3）y2－4ty－2=0.
解得
（12分）
故直线m的方程为
（13分）
22．解：（1）令a = b = 0，得
令a = b
= 1，得
，
2分
（2）令
令
是奇函数.
5分
（3）当
令
，
7分
即
，
10分
又S1=1
故存在关于n的整式g (n)=n，使等式对于一切不小于2的自然数n恒成立 12分