高三数学第二次联考试题（理科）
一、选择题（50分）
1.设集合A=｛a，b｝，则满足A
B=｛a,b,c,d｝的所有集合的个数是（ ）
A.1 B.4 C.8 D.16
2.等差数列｛an｝前n项和为Sn，且 a8+a16=0,则有（ ）
A.S8＜S16 B.S8=S16 C.S7＜S16 D.S7 = S16
3.平面上不共线的四点A，B，C，D，若
则
△ABC的形状为（ ）
A.直角三角形 B.等腰三角形 C.等边三角形 D.等腰直角三角形
4.函数y=asinx+2bcosx图像的一条对称轴方程为x=
，则直线ax+by+1=0与直线x+y+2=0的夹角为（
）
A.arctan3 B. arctan
C.
arctan2 D. arctan
5.设随机变量
～N（
，
2），且P（＜1）=,P（＞2）=p,则P（0＜＜1）=（ ）
A. p
B.1-p
C.1-2p D. -p
6.某圆以
原点为圆心，经过双曲线
的焦点，且被该双曲线的右准线分为弧长为1﹕2的两段圆弧，那么该双曲线的离心率为（ ）
A.
B.
C.
D.
7.已知（1+x）+（1+x）2+（1+x）3+…+（1+x）n=a0+a1x+a2x2+…+anxn,a1+a2+…+an-1=29-n,(n
N且n＞1)，那么（1+y）6的展开式中含yn的项的系数为
A.1 B.6 C.15 D.20
8.函数y=f（x）的图像过原点，且它的导函数f′（x）的图像是如图所示的一条直线，则y=f（x）的图像的顶点在（ ）
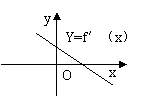A.第一象限 B. 第二象限
C.第三象限 D. 第四象限
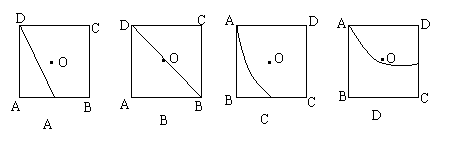
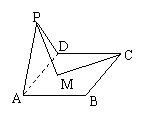9.如右图，△ADP为正三角形，四边形ABCD为正方形，平面PAD⊥面ABCD.M为平面ABCD内的动点，且满足MP=MC，则点M在正方形ABCD内的轨迹为（O为正方形ABCD的中心）（ ）
10.已知定义域为R的函数f（x）满足f（-x）=－f（x+6），当x＞3时，f（x）单调递增，若x1+x2＜6且（x1-3）（x2-3）＜0，则f（x1）+f（x2）的值（ ）
A.恒为0 B.恒小于 0 C.恒 大于0 D.可正可负
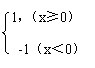二、填空题（共25分）
11.若函数f（x）=
，则不等式xf（x）+x≤0的解集为_________.
 |
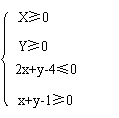12.已知实数x，y满足 ，则z=x2+（y+2）2的最小值为_________.
 |
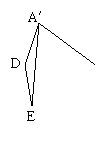13.如图，矩形ABCD中，AB=2CD=2，且E为AB的中点，
将△ADE沿DE折起，使平面A′DE⊥平面EBCD，则A′C
与平面EBCD所成角的正切值等于__________.
14.2006年12月1日，国内版“城市之间”南北十强决赛在海口市拉开帷幕，我省有衡阳，岳阳，郴州三市参与决赛，为满足活动的需要，海口市共准备了四个宾馆以供各代表团入住，假定每个代表团可入住任一宾馆，且入住各个宾馆是等可能的，则我省三个代表团恰好分住其中三个不同宾馆的概率为__________.
15.对于实数x≥0，定义符号[x]表示不超过x的最大整数，则方程[2sinx]=[x]的解集是（x以弧度为单位）___________.
三、解答题（共75分）
16.（12分）已知向量
=
=（cos
，sin），
，
其中O为坐标原点，且
（1）若
求
的值；
（2）若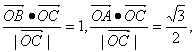
求△OAB的面积S.
17.（12分）袋中装着标有数字1，2，3，4，5的小球各2个，从袋中任取3个小球，按3个小球上最大数字的9倍计分，每个小球被取出的可能性都相等，用表示取出的3个小球上的最大数字.
（1）取出的3个小球上的数字互不相同的概率；
（2）随机变量的概率分布和数学期望；
（3）计分介于20分到40分之间的概率.
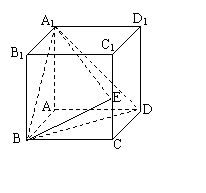
18.（12分）如图，在正方体ABCD－A1B1C1D1中，点E在棱 CC1上.
（1）求证： A1E⊥BD；
（2）当A1E与面BED所成角 为多大时，面A1BD⊥面EBD；
（3）在（2）的结论下，求此时二面角A－A1D－E的大小.
 |
19.（12分）已知B（1，b）为函数f（x）=x3+ax2+1的图像上一点，过B（1，b）的切线斜率为－3.
（1）求a,b的值；
（2）若不等式f（x）≤
－1990对于x[－1，4]恒成立，试求的取值范围；
（3）设g（x）+f（x）=－3x2+tx+1，问： 是否存在实数t，使得当 x
（0，1]时，g（x）有最大值1？
20.（13分）如图，F是抛物线y2=4x的焦点，Q为准线与x轴的交点，直线l经过点Q.
（1）直线l与抛物线有唯一公共点，求l的方程；
（2）直线l与抛物线交于A，B两点，
①记FA，FB的斜率分别为k1，k2.求证：k1+k2为定值；
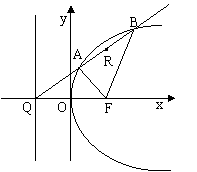②若点R在线段AB上，且满足
求点R的轨迹方程.
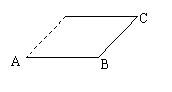
21.（14分）如图，将圆分成标有1，2，…，n的n个具有不同标号的扇形区域，用3种不同颜色给每一个扇形区域染色，要求相邻区域颜色互异，把不同的染色方法种数记为an.求：
（1）a1,a2,a3,a4;
（2）an与an+1(n≥2)的关系式；
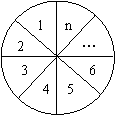（3）数列｛an｝的通项公式an,并证明an≥2n（nN*）.
参考答案
一、选择题
1.B 2.D 3.B 4.B 5.D 6.D 7.C 8.A 9.A 10.B
二、填空题
11.｛xx≤0｝
12.5 13.
14.
15.[0，
）[1，
）（，2）
三、解答题
16.（1）
（2）S=1
17.（1）
（2）E=
（3）
18.（1）略
（2）arcsin
（3）arccos（－）
19.（1）a=－3,b=－1; （2）≥2007 （3）t=
20.（1）y=0;y=x+1;y=－x－1;（2）1.k1+k2=0;
2.x=1（－2＜y＜2且y≠0）
21.（1）a1=3,a2=6,a3=6,a4=18;
（2）an+an+1=3×2n;
（3）an=2n+2·（－1）n.