高三数学高考模拟试卷2
一、选择题
1、若α、β终边关于y轴对称,则下列等式成立的是( )
A、sinα=sinβ B、cosα=cosβ C、tanα=tanβ D、cotα=cotβ
2、已知一物体在共点力F1=(lg2,lg2),F2=(lg5,lg2)的作用下产生位移S=(2lg5,1),则共点力对物体做的功W为( )
A、lg2 B、lg5 C、1 D、2
3、△ABC中,3sinA+4cosB=6,3coA+4sinB=1,则∠C的大小是( )
A、![]() B、
B、![]() C、
C、![]() 或
或![]() D、
D、![]() 或
或![]()
4、已知![]() 的分布列为
的分布列为
|
| -1 | 0 | 1 |
| P |
|
|
|
且设![]() ,则
,则![]() 的期望值是( )
的期望值是( )
A、![]() B、-
B、-![]() C、1
D、
C、1
D、![]()
5、等差数列{an}中,S9=-36,S13=-104,等比数列{bn}中,b5=a5,b7=a7,则b6=( )
A、![]() B、-
B、-![]() C、±
C、±![]() D、无法确定
D、无法确定
6、若直线2ax-by+2=0(a,b∈R)始终平分圆x2+y2+2x-4y+1=0的周长,则ab的取值范围是( )
A、(-∞,![]() ] B、(0,
] B、(0,![]() ] C、(0,
] C、(0,![]() ) D、(-∞,
) D、(-∞,![]() )
)
7、如果一个平面与一个正方体的十二条棱所在的直线都成相等的角,记作θ,那么sinθ的值为( )
A、![]() B、
B、![]() C、
C、![]() D、1
D、1
8、若动点P、Q是椭圆9x2+16y2=144上的两点,O是其中心,若![]() ,则中心O到统PQ的距离OH必为( )
,则中心O到统PQ的距离OH必为( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
9、函数f(x)的反函数图像向左平移1个单位,得到曲线C,函数g(x)的图象与曲线C关于y=x成轴对称,那么g(x)等于( )
A、g(x)=f(x)-1 B、g(x)=f(x+1)
C、g(x)=f(x)+1 D、g(x)=f(x-1)
10、将两邻边长之比为3:4的长方形ABCD沿对角线AC折成一个直二面角,若四点A、B、C、D的外接球的球面面积为100π,则B、D两点间的球面距离为( )
A、![]() B、
B、![]() C、
C、![]() D、3
D、3![]()
11、已知集合A={12,14,16,18,20},B={11,13,15,17,19},在A中任取一个元素用ai(i=1,2,3,4,5)表示,在B中任取一个元素用bj(j=1,2,3,4,5)表示,则所取两数满足ai>bI的概率为( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
12、生物学指出,生态系统中,在输入一个营养级的能量中,大约10%-20%的能量流动到下一个营养级,在H1→H2→H3→4→H5→H6,这条生物链中,若能使H6获得10J的热量,则需要H1最多可提供的能量是( )
A、104kJ B、105kJ C、106kJ D、107kJ
二、填空题
13、若把抛物线y=2x2绕其顶点逆时针方向转动90°,则转动后所得的抛物线的焦点坐标为 。
![]() 14、设 ABCD的对角线交于点O,且
14、设 ABCD的对角线交于点O,且![]() ,
,![]() ,则
,则![]() = 。
= 。
15、某校准备召开高中毕业生代表会,把6个代表名额分配给高三年级的3个班,每班至少一个名额,不同的分配方案共有 种。
16、已知函数f(n)=![]() (n∈N),则
(n∈N),则![]() = 。
= 。
三、解答题
17、已知向量![]() =3i-4j,
=3i-4j,![]() =6i-3j,
=6i-3j,![]() =(5-m)I-(3+m)j,其中i、j分别是直角坐标系内x轴与y轴正方向上的单位向量。
=(5-m)I-(3+m)j,其中i、j分别是直角坐标系内x轴与y轴正方向上的单位向量。
①若A、B、C能构成三角形,求实数m应满足的条件;
②若△ABC为直角三角形,且∠A为直角,求实数m的值。
18、已知数列{an}的前n项之和为Sn,且Sn=a(an-1)(a≠0,a≠1,n∈Nn)
(1)求数列{an}的通项公式;
(2)数列{bn}=2n+b(b是常数),且a1=b1,a2>b2,求a的取值范围。
19、如图,在三棱锥P-ABC中,PA⊥底面ABC,△ABC为正三角形,D、E分别是BC、CA的中点。
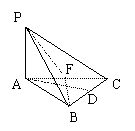 (1)证明:平面PBE⊥平面PAC;
(1)证明:平面PBE⊥平面PAC;
(2)如何在BC上找一点F,使AD//平面PEF?并说明理由;
(3)若PA=AB=2,对于(2)中的点F,求三棱锥B-PEF的体积。
20、某种细菌两小时分裂一次,(每一个细菌分裂成两个,分裂所需的时间忽略不计),研究开始时有两个细菌,在研究过程中不断进行分裂,细菌总数y是研究时间t的函数,记作y=f(t)
(1)写出函数y=f(t)的定义域和值域;
(2)在所给坐标系中画出y=f(t);(0≤t<6)的图象;
 (3)写出研究进行到n小时(n≤0,n∈Z)时细菌的总数有多少个(用关于n的式子表示)。
(3)写出研究进行到n小时(n≤0,n∈Z)时细菌的总数有多少个(用关于n的式子表示)。
21、已知椭圆C:![]() ,它的离心率为
,它的离心率为![]() ,直线
,直线![]() :y=x+2,它与以原点为圆心,以C1的短半轴长为半径的圆相切。
:y=x+2,它与以原点为圆心,以C1的短半轴长为半径的圆相切。
(1)求椭圆C1的方程;
(2)设椭圆C1的左焦点为F,左准线为![]() 。动直线
。动直线![]() 垂直于
垂直于![]() ,垂足为P,线段PF的垂直平分线交
,垂足为P,线段PF的垂直平分线交![]() 交于点M。点M的轨迹C2与x轴交于点Q,若R、S两点在C2上,且满足QR⊥RS,求QS的取值范围。
交于点M。点M的轨迹C2与x轴交于点Q,若R、S两点在C2上,且满足QR⊥RS,求QS的取值范围。
22、设函数f(x)=sin2x+![]() )
)
(1)求f(x)的最大值M(a)。
(2)当a∈[-1,1]时,求函数M(a)的最值。
【答案】
1、A 2、D 3、A 4、A 5、C 6、A 7、B 8、C 9、A 10、C 11、B 12、C
13、(![]() ,0) 14、
,0) 14、![]() 15、10
16、1
15、10
16、1
17、①当m≠![]() 时,A、B、C三点能构成三角形;
时,A、B、C三点能构成三角形;
②当m=![]() 时,三角形ABC为直角三角形,且∠A=90°。
时,三角形ABC为直角三角形,且∠A=90°。
18、(1)![]() (2)
(2)![]()
19、(1) ∵PA⊥底面ABC,∴PA⊥BE
又∵△ABC是正三角形,且E为AC的中点,∴BE⊥CA
又PA![]() ,∴BE⊥平面PAC
,∴BE⊥平面PAC
∵BE![]() 平面PBE,∴平面PBE⊥平面PAC。
平面PBE,∴平面PBE⊥平面PAC。
(2)取CD的中点F,则点F即为所求。
∵E、F分别为CA、CD的中点,∴EF//AD
又EF![]() 平面PEF,AD
平面PEF,AD![]() 平面PEF,∴AD//平面PEF。
平面PEF,∴AD//平面PEF。
(3)![]()
20、 (1)函数y=f(t)的定义域为[0,+∞);值域为{yy=2n,n∈N*}
 (2)
(2)
(3)y=
 21、(1)由
21、(1)由![]() ,得
,得![]()
∵直线![]() :y=x+2与圆x2+y2=b2相切,∴
:y=x+2与圆x2+y2=b2相切,∴![]() ,解得
,解得![]() ,则a2=3。
,则a2=3。
故所求椭圆C1的方程为![]() 。
。
(2)椭圆C1的左焦点为F(-1,0),左准线为![]() :x=-3。
:x=-3。
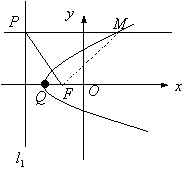
如图,连结MF,则MF=MP,∴点M的轨迹C2是以F为焦点,![]() 为准线的抛物线,其方程为y2=4(x+2),故Q(-2,0)。设
为准线的抛物线,其方程为y2=4(x+2),故Q(-2,0)。设![]() 、
、![]() ,由QR⊥RS得
,由QR⊥RS得
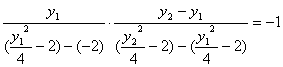
化简得y2=-(y1+![]() )
)
∴y22=y12+![]() ≥2×16+32=64
≥2×16+32=64
∵QS2=[(![]() -2)+2]2+y22=
-2)+2]2+y22=![]()
∴当y22=64时,QSmin=![]() .
.
故QS的取值范围是[8![]() ,+∞)。
,+∞)。
22、解:(1)由f(x)=-(cosx-a)2+a3+a2-a+1
令t=cosx,![]() ,
0≤t≤1
,
0≤t≤1
则g(t)=-(t-a)2+a3+a2-a+1
10若a<0,则当t=0时,M(a)=g(0)=a3-a+1
20若0≤a≤1,则当t=a时,M(a)=g(a)=a3+a2-a+1
30若a>1,则当t=1时,M(a)=g(1)=a3+a
∴M(a)=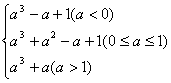
(2)当-1≤a<0时,M(a)=a3-a+1
∴M’(a)=![]() )(a-
)(a-![]() )
)
令M’(a)=0,得a1=-![]() ,或a2=
,或a2=![]() (舍去)
(舍去)
且M(-![]() )=(-
)=(-![]() )3-(-
)3-(-![]() )+1=
)+1=![]() +1
+1
当0≤a<1时,M(a)=a3+a2-a+1
∴M’(a)=3a2+2a-1=(3a-1)(a+1)
令M’(a)=0,得a3=![]() ,或a4=-1(舍去)
,或a4=-1(舍去)
且M(![]() )=(
)=(![]() )3+(
)3+(![]() )2-
)2-![]() +1=
+1=![]()
列表如下
| a | -1 | (1,- | - | (- | 0 | (0, |
| ( | 1 |
| M’(a) | + | - | + | ||||||
| M(a) | 1 |
| 1 |
| 2 |
从上表可知:
当a=1时,M(a)取得最大值2
当a=![]() 时,M(a)取得最小值
时,M(a)取得最小值![]() 。
。