高三数学摸底测试
一、选择题：本大题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.
1.(理)已知全集I=R，集合A={xy=
}，集合B={x0＜x＜2}，则(
A)∪B等于( )
A.[1，+∞) B.(1，+∞)
C.[0，+∞) D.(0，+∞)
(文)已知全集I=R，集合A={xx≤1}，集合B={x0＜x＜2}，则(A)∪B等于( )
A.[1，+∞) B.(1，+∞)
C.[0，+∞) D.(0，+∞)
2.在等差数列{an}中，若a1+a2=3，a3+a4=5，则a7+a8的值为( )
A.7 B.8 C.9 D.10
3.函数f(x)=log2(x+1)(x＞0)的反函数是( )
A.f-1(x)=2x-1(x∈R) B.f-1(x)=2x-1(x∈R)
C.f-1(x)=2x-1(x＞0) D.f-1(x)=2x-1(x＞0)
4.已知a、b、c∈R，则“a＞b”是“ac＞bc”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
5.(理)已知函数f(x)=a-x(a＞0，a≠1)，且f(3)=8，则( )
A.f(2)＞f(-2) B.f(-3)＞f(-2)
C.f(1)＞f(2) D.f(-3)＞f(-4)
(文)下列函数中，在其定义域内既是奇函数又是减函数的是( )
A.y=-x
(x∈R) B.y=(
)x (x∈R)
C.y=-x3-x (x∈R) D.y=
(x∈R，x≠0)
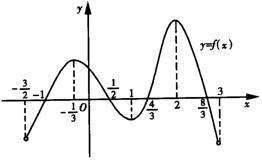
6.(理)函数y=f(x)在定义域(
，3)内可导，其图像如图所示.记y=f(x)的导函数为y=f′(x)，则不等式f′(x)≤0的解集为( )
A.[
，1]∪[2，3) B.[-1，
]∪[
]
C.[
]∪[1，2) D.(]∪[
]∪[
，3)
(文) 已知函数f(x)=a-x(a＞0，a≠1)，且f(3)=8，则( )
A.f(2)＞f(-2) B.f(-3)＞f(-2)
C.f(1)＞f(2) D.f(-3)＞f(-4)
7.某采访小组共8名同学，其中男生6名，女生2名.现从中按性别分层随机抽取4名同学参加一项采访活动，则不同的抽取方法共有( )
A.40种 B.70种 C.80种 D.240种
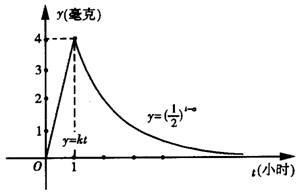
8.某医药研究所开发一种新药，如果成年人按规定的剂量服用，据检测，服药后每毫升血液中的含药量y(毫克)与时间t(小时)之间的关系用如图所示曲线表示.据进一步测定，每毫升血液中含药量不少于6.25毫克时，治疗疾病有效.则服药一次治疗该疾病有效的时间为( )
A.4小时 B.
小时 C.
小时 D.5小时
二、填空题：本大题共6小题，每小题5分，共30分.把答案填在题中横线上.
9.(理)复数
的值等于___________________.
(文)在(x2+
)6的展开式中常数项的值是_________________.
10.(理)等比数列{an}中，a3=8，S5=S3+16，S5的值等于____________.
(文)已知等比数列{an}中，an＞0，n=1，2，3，…，a2=2，a4=8，则前5项和S2的值为_________.
11.(理)若(x2-
)n的展开式中含有常数项，则正整数n的最小值是_______________.
(文)函数y=log2(x+)的最小值是___________________.
12.(理)
的值等于__________________
(文)如果学生甲每次投篮投中的概率为，那么他连续投三次，恰好两次投中的概率为_____________，至少有一次投中的概率为_____________.(用数字作答)
13.(理) 如果学生甲每次投篮投中的概率为，那么他连续投三次，恰好两次投中的概率为_____________，至少有一次投中的概率为_____________.(用数字作答)
(文)函数y=g(x)的图像与f(x)=ax-1的图像关于直线y=x对称，若g(x)的图像过点(2，4)，则g(a-1)的值为______________.
14.函数y=x2-5x+10的定义域为(n，n+1]，值域为Dn，n=1，2，3，….若将Dn中整数的个数记为an，则a1的值为__________；数列{an}的通项公式为____________.
三、解答题：本大题共6小题，共肋分.解答应写出文字说明，证明过程或演算步骤.
15.(本小题共12分)
已知集合A={x
＜1}，B={xx2＞5-4x}，C={xx-m＜1，m∈R}
(Ⅰ)求A∩B；
(Ⅱ)若(A∩B)
C，求m的取值范围.
16.(本小题共13分)
已知函数f(x)=x3+ax2+2，x=2是f(x)的一个极值点.求：
(Ⅰ)实数a的值；
(Ⅱ)f(x)的区间[-1，3]上的最大值和最小值.
17.(本小题共13分)
(理)某学校举办一场以“为希望工程献爱心”为主题的图书义卖活动.同学甲随机地从10本书中买两本，假设每本书被甲同学买走的概率相同.已知这10本书中有3本单价定为10元，4本单价定为15元，3本单价定为20元.记甲同学买这两本书所付金额为ξ(元).求：
(Ⅰ)随机变量ξ的分布列；
(Ⅱ)随机变量ξ的期望Eξ.
(文)已知{an}为等差数列，且a1=1，{bn}为等比数列，数列{an+bn}的前三项依次为3，7，13.求：
(Ⅰ)数列{an}，{bn}的通项公式；
(Ⅱ)数列{an+bn}的前n项和Sn.
18.(本小题共14分)
(理)已知函数f(x)=ln(x2+1)-ax(a∈R).
(Ⅰ)若函数f(x)在R上是增函数，求a的取值范围；
(Ⅱ)若a＜1，求f(x)的单调增区间.
(文)已知袋中有编号为1-9的小球各一个，它们的大小相同，从中任取三个小球.求：
(Ⅰ)恰好有一球编号是3的倍数的概率；
(Ⅱ)至少有一球编号是3的倍数的概率；
(Ⅲ)三个小球编号之和是3的倍数的概率.
19.(本小题共14分)
(理)设数列{an}的前n项和为Sn，且满足Sn=2-an，n=1，2，3，….
(Ⅰ)求数列{an}的通项公式；
(Ⅱ)若数列{bn}满足b1=1，且bn+1=bn+an，求数列{bn}的通项公式；
(Ⅲ)设cn=n(3-bn)，求数列{cn}的前n项和Tn.
(文)已知函数f(x)=
.
(Ⅰ)当a=-3时，求函数f(x)的单调递增区间；
(Ⅱ)若函数f(x)在区间(-∞，0)上至少有一个极值，求实数a的取值范围.
20.(本小题共14分)
(理)设函数f(x)=ax2+bx+c，a、b、c都是正实数，且f(1)=1.
(Ⅰ)若x＞0，证明：f(x)·f()≥1；
(Ⅱ)若正实数x1、x2、x3满足x1·x2·x3=1，证明：f(x1)·f(x2)·f(x3)≥1.
(文)设数列{an}的前n项和为Sn，且满足Sn=2-an，n=1，2，3，….
(Ⅰ)求数列{an}的通项公式；
(Ⅱ)若数列{bn}满足b1=1，且bn+1=bn+an，求数列{bn}的通项公式；
(Ⅲ)设cn=n(3-bn)，数列{cn}的前n项和为Tn，求证：Tn＜8.