高考数学仿真卷三（文）
（湖南卷）
一、选择题：本大题共10小题，每小题5分，共50分. 在每小题给出的四个选项中，只有一项是符合题目要求的.
1．命题“若
，则
”的否命题是
（ ）
A．若，则
B．若，则
C．若
，则
D．若，则
2．非零向量
不共线，若
+
=
，-=
，则⊥是=的
（ ）
A、充要条件 B、充分不必要条件
C、必要不充分条件 D、既不充分又不必要条件
3．图像
与函数
的图像关于（ ）
A．直线
对称 B．点
对称 C．直线
对称 D．点
对称
4．在△ABC中，若sin A = cos Bcos C，则tan C+tan B的值为（ ）
A． 1 B．—1 C．－2 D．2
5．设f(x)=x2-6x+5，若实数x、y满足条件
则
的最大值是（ ）
A．9-4
B.3 C.5 D.4
7．将
的图象上所有的点的横坐标扩大为原来的2倍（纵坐标不变），得到
的图象，再将的图象按向量平移，得到
的图象，
则=（ ）
A．（
，1） B．（-，1） C．（
，-1） D．（-，-1）
8．若直线mx＋ny＝4和⊙O∶
没有交点，则过（m，n）的直线与椭圆
的交点个数 （ ）
A．至多一个 B．2个
C．1个 D．0个
9．已知棱长都相等的正三棱锥内接于一个球，某人画出四个过球心的平面截球与正三棱锥所得的图形如下，则 （ ）
A.以下四个图形都是正确的 B.只有（2）（4）是正确的 C.只有（4）是正确的 D.只有（1）（2）是正确的
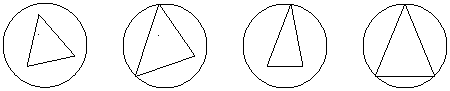
① ② ③ ④
10．直线x=m，y=x将圆面
分成若干块，现用5种颜色给这若干块涂色，每块只涂一种颜色，且任意两块不同色，共有120种涂法，则m的取值范围是 （ ）
A．
B．
C．
D 
二．填空题：本大题共5小题，每小题5分，共25分。把答案填在答题卡的相应位置
11．设
中所有项的系数和
12．已知椭圆
（a＞b＞0）与双曲线
（m＞0，n＞0）有相同的焦点（-c，0）和（c,0），若c是 a与m的等比中项，n2是2m2与c2的等差中项，则椭圆的离心率是
13．有8个大小相同的球，上面分别标有1、2、3、4、5、6、7、8，现任取三个球，则恰有两个球的序号相邻的取法有
14．数列
满足
（
且
），
，
是的前
次和，则为
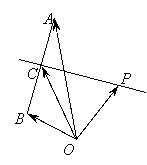
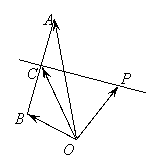
15如图，
是平面上的三点，向量
a， 
b,
设
为线段
的垂直平分线
上任意一点，向量
p若a=4，b=2，则p（a 
b）等于
三．解答题：本大题共6小题，共75分。解答应写出文字说明，证明过程或演算步骤。
16．（本小题满分12分）
内接于以O为圆心，1为半径的圆，且
．
（1）求数量积
，
，
；（2）求的面积．
17．（本小题满分12分）有甲.乙.丙三人玩掷骰子放球的游戏,若掷出1点,甲获得一球；若掷出2点或3点,乙获得一球；若掷出4点，5点或6点获得一球.设掷n次后,甲,乙,丙获得的球数分别为x,y,z.
(Ⅰ)当n=3时,求x,y,z成等差数列的概率；
（Ⅱ）当n=6时，求x,y,z成等比数列的概率。
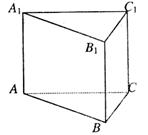
18．（本小题满分12分）已知正三棱柱ABC—A1B1C1的底边长为1，高为h(h>3)，点M在侧棱BB1上移动，到底面ABC的距离为x，且AM与侧面BCC1所成的角为α；
|
,求α
（Ⅱ）若
所成的角.
19．（本小题满分12分）已知函数f(x)=
，设正项数列{an}的首项a1=2,前n 项和Sn满足Sn=f(Sn-1)(n>1,且n∈N*);
(1)求an的表达式；
(2)在平面直角坐标系内，直线Ln的斜率为an,且Ln与曲线y=x2有且仅有一个公共点，Ln又与y轴交于点Dn(0,bn),当n∈N*时，记dn=
-1，若Cn=
,求证：C1+C2+C3+…+Cn-n<1.
20．（本小题满分13分）已知f（x）＝x3－3x，若m2－4n>0，m，n∈R，求证：“2m＋n<4”是“方程[f（x）]2＋mf（x）＋n＝0在区间（－1，1）内有两个不等的实根”的充分不必要条件．
21．（本小题满分13分）在直角坐标系中，O为坐标原点，F是x轴正半轴上的一点，若△OFQ的面积为S，且
.
（Ⅰ）（本问6分）设
若以O为中心，F为焦点的椭圆经过点Q，求
的最小值以及此时的椭圆方程；
（Ⅱ）
| |
的弦AB的两个端点在椭圆E上滑动，M为线段AB的中点，求M点到椭圆右准线距离的最大值及对应的AB直线的方程.
高考数学仿真卷三（文）参考答案
（湖南卷）
一、选择题：
| 提次 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ||
| 答案 | C | A | B | A | C | B | D | B | D | A |
提示
2 法一：⊥
•=（+）•（-）= 2 - 2 = 0 = ，选故C
法二：作
，
，以
，
为邻边作平行四边形OACB，则=
，=
. ⊥
为菱形 = .选故A
3． 
可见，当点（x,y）在的图象上时，其关于点（1，0）的对称点在的图象上，故两图象关于点对称。选故B
4．
tan C+tan B=
选故A
5 原不等式组等价于
作出可行域如右图.令
，即y=kx,知当此直线过
点A(1，5)时，k有最大值.∴k=5,选C
6。过 P的直线可以与L 异面垂直.故不一定在
内，选B
7． 
，即
，变换到，须按向量
平移。选D
8．
由直线mx＋ny＝4和⊙O∶没有交点
故选B。
9．，球心在正三棱锥的高上。故选D。
10．
。因涂法有120种，所以圆面分成4块，故选A。
二．填空题：
| 题次 | 11 | 12 | 13 | 14 | 15 |
| 答案 |
|
| 30 |
| 6 |
提示
13．．分类讨论，（1）1与2相邻或7与8相邻时，各有5种取法，共10种。（2）2与3，3与4，4与5，5与6，6与7各有4种取法，共20种取法。所以总共有30种取法。
14．显然是一个等和数列，即
形如： 
，1，，1,…… ∴
15
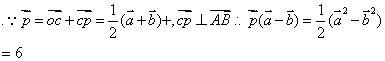
三．解答题：
16解：（1）∵
，由条件可得
两边平方得
∴
．
……（2分）
同理可得
，
．
……（6分）
（2）由可得
，∴
由，得
，∴
，
∴
，
……（8分）
由，得
，∴
，
∴
，
……（10分）
即可得
．
……（12分）
17．解 （Ⅰ）因为x+y+z=3，2y=x+z
所以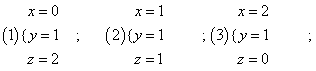
2分
（1）
表示 ：掷3次，1次出现2点或3点，2次出现4点或5点或6点，共三种情况。所以x=0，y=1，z=2的概率为
4分
（2）
表示：掷3次，1次出现1点，1次出现2点或3点，1次出现4点或5点或6点共有6种情况。所以x=y=z=1的概率为
6分
同理x=2，y=1，z=0的概率为
8分
所以当n=3时，求x，y，z成等差数列的概率为
9分
（Ⅱ）当n=6时，x，y，z成等比数列，所以x=y=z=2，所求概率为
12分
18．解：（I）设BC的中点为D，连结AD、DM，在正△ABC中，易知AD⊥BC，又侧面BCC1与底面ABC互相垂直，∴AD⊥平面BCC1，即∠AMD为AM与侧面BCC1所成的角，∴∠AMD=α，3分
∴在Rt△ADM中，cosAMD=
依题意BM即为点B到度面ABC的距离，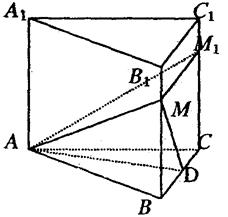
∴BM=x，4分
且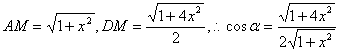
，
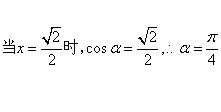6分
（II）
8分
19．解：(1)由Sn=
得
2分
所以数列
是以
为公差的等差数列，3分
∴
Sn=2n2,an=Sn-Sn-1=4n-2(n≥2),又a1=2∴an=4n-2(n∈N*).5分
(2)设Ln：y=anx+bn,由
6分
据题意方程有相等实根，∴△=a
，7分
∴bn=-
8分
当n∈N*时，dn=
9分
∴Cn=
10分
∴c1+c2+c3+…+cn-n=n+
11分
. 12分
20解：由f（x）＝x3－3x得f′（x）＝3（x2－1），对x∈（－1，1）有f′（x）<0，故f（x）在（－1，1）上力减函数，得f（x）∈（－2，2）． （3分）
于是“方程[f（x）]2＋mf（x）＋n＝0在区间（－1，1）内有两个不等的实根”等价于“方程g（t）＝t2＋mt＋n＝0在区间（－2，2）内有两个不等的实根”． （5分）
所以“方程[f（x）]2＋mf（x）＋n＝0在区间（－1，1）内有两个不等的实根”等价于
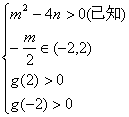（8分）
下面先证明充分性：由2m＋n<4得m<4
－2<
<2，
且4>±2m－n，即g（±2）>0．所以充分性成立． （10分）
下面再证不必要性：取m＝2,n＝
,显然满足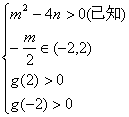
但是2m＋n<4不成立，即得不必要性成立．
综合以上得命题成立． （13分）
21解：（I） 设椭圆的方程是
，Q点的坐标设为（x1，y1），1分
则
∵△OFQ的面积是
3分
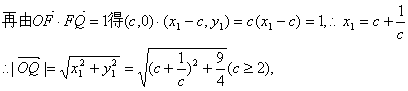4分
显然当且权当c=2时
有最小值，其最小值是3，5分
此时Q点的坐标是
，代入椭圆方程是
，
解得a2=10,b2=6，∴所求椭圆方程是
.6分
（II）由（I）椭圆方程，椭圆的左焦点为F1（－2，0），
欲求M点到右准线距离的最大值，可求该点到左准线距离的最小值，7分
设A、B、M点在左准线的射影分别为A′、B′、M′，由椭圆第二定义及梯形中位线性质得：
8分
由
即M点到左准线距离的最小值为2，此时A、F1、B三点共线，
9分
设过F1的直线方程为x=hy－2，将其与椭圆方程联立，
消去x得（3h2+5）y2－12hy－18=0，
∴y1+y2=
，此时中点M的纵坐标为y0=
,
故得M点的横坐标为x0=－2， 10分
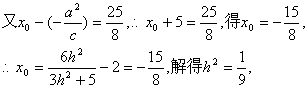12分
∴所求的直线方程为x=
y－2，即3x－y+2=0或3x+y+2=0 13分