高考数学模拟试卷(文)
何小菊
一、选择题
1.若p、q为简单命题,则“p且q为假”是“p为假”的( )
A.充分不必要的条件 B.必要不充分的条件
C.充要条件 D.既不充分也不必要的条件
2.直线y=x+2与圆![]() (
(![]() 为参数)的交点个数为 ( )
为参数)的交点个数为 ( )
A.0个
B.1个
C.2个
D.与![]() 的取值有关
的取值有关
3.若函数![]() 的反函数
的反函数![]() ,则
,则![]() ( )
( )
A.1 B.-1 C.1或-1 D.5
4. 如果a,b,c成等比数列,那么关于x的方程ax2+bx+c=0 ( )
A.一定有两个不相同的实数根 B.一定有两个相同的实数根
C.一定没有实数根 D.以上三种情况均可出现
5. 设![]() 、
、![]() 是不同的直线,
是不同的直线,![]() 、
、![]() 、
、![]() 是不同的平面,有以下四个命题:
是不同的平面,有以下四个命题:
(1)![]() ; (2)
; (2)![]() ;
;
(3)![]() ; (4)
; (4)![]() ,其中,假命题是( )
,其中,假命题是( )
A.(1)(2) B.(2)(3) C.(1)(3) D.(2)(4)
6 . 已知O是△ABC内一点,且满足![]() ,则O点一定是△ABC
,则O点一定是△ABC
的 ( )
A.内心 B.外心 C.垂心 D.重心
7.设双曲线以椭圆![]() 长轴的两个端点为焦点,其准线过椭圆的焦点,则双曲线的渐近线的斜率为 ( )
长轴的两个端点为焦点,其准线过椭圆的焦点,则双曲线的渐近线的斜率为 ( )
A.±2 B.![]() C.
C.![]() D.
D.![]()
8.在R上定义运算![]() :
:![]() .若不等式
.若不等式![]() 对任意实数
对任意实数![]() 成立,则 a的取值范围
( )
成立,则 a的取值范围
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9.函数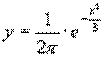 的部分图象大致是
( )
的部分图象大致是
( )
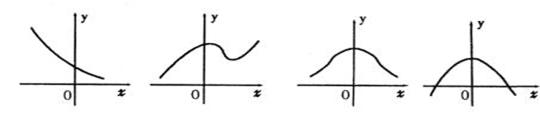
A. B. C. D.
10.用0、1、2、3、4这五个数字组成无重复数字的五位数,其中恰有一个且只有一个偶数数字夹在两个奇数数字之间的五位数的个数是( )
A.48 B.36 C.28 D.12
二.、填空题
11.过点(1, 0)作曲线![]() 的切线,则切线斜率为 _▲__
的切线,则切线斜率为 _▲__
12. 在三角形ABC中,sinA : sinB : sinC=2:3:4,则cosC的值为____▲____________.
13. 已知![]() 的展开式中
的展开式中![]() 的系数与
的系数与![]() 的展开式中x3的系数相等,则
的展开式中x3的系数相等,则![]() = _▲__ .
= _▲__ .
14. 以下四个关于圆锥曲线的命题中
①设A、B为两个定点,k为非零常数,![]() ,则动点P的轨迹为双曲线;
,则动点P的轨迹为双曲线;
②过定圆C上一定点A作该圆的动弦AB,O为坐标原点,若![]() 则动点
则动点![]() 的轨迹为椭圆;
的轨迹为椭圆;
③方程![]() 的两根可分别作为椭圆和双曲线的离心率;
的两根可分别作为椭圆和双曲线的离心率;
④双曲线![]() 有相同的焦点.
有相同的焦点.
其中真命题的序号为 _▲__ (写出所有真命题的序号)
三、解答题
15.设函数f(x)=![]()
(1) 求ω的值并判断函数![]() 的奇偶性.
的奇偶性.
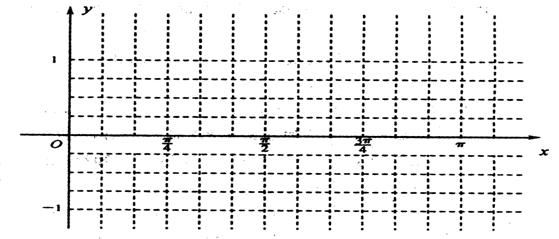
(2) 画出函数![]() 在区间[0,π]上的图象.
在区间[0,π]上的图象.
 |
.
16.如图,三棱锥![]() 中,
中,![]() ,
,
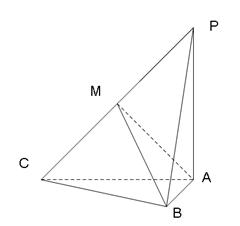
![]() .
.
(1)求证:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的大小;
的大小;
(3)若![]() 为线段
为线段![]() 上的点,设
上的点,设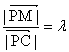 ,
,
问![]() 为何值时能使直线
为何值时能使直线![]()
![]() 平面
平面![]() 。
。
17.数列![]() 的前项
的前项![]() 和记为
和记为![]() ,数列
,数列![]() 是首项为2,公比也为2的等比数列.
是首项为2,公比也为2的等比数列.
(1)求![]() ;
;
(2)若数列![]() 的前
的前![]() 项和不小于100,问此数列最少有多少项?
项和不小于100,问此数列最少有多少项?
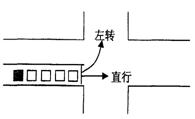
18.
|
此时前方交通灯为红灯,且该车前面已有4辆车
依次在同一车道上排队等候(该车道只可以
直行或左转行驶). 已知每辆车直行的概率
是![]() ,左转行驶的概率是
,左转行驶的概率是![]() ,该路口红绿灯
,该路口红绿灯
转换间隔时间均为1分钟. 假设该车道上一
辆直行去临安的车驶出停车线需要10秒钟,一辆左转去小和山的车驶出停车线需要20秒钟,求:
(1)前4辆车恰有2辆车左转行驶的概率;
(2)该车在第一次绿灯这亮起时的1分钟内通过该路口的概率(汽车驶出停车线就算通
过路口)。
19.设函数![]() 。
。
(1)若![]() 处取得极值,求常数a的值;
处取得极值,求常数a的值;
(2)若![]() 上为增函数,求a的取值范围。
上为增函数,求a的取值范围。
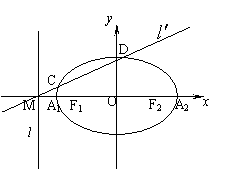
20.如图,已知椭圆的中心在坐标原点,焦点![]() 在
在![]() 轴上,长轴
轴上,长轴![]() 的长为4,左准线
的长为4,左准线![]() 与
与![]() 轴的交点为M,
轴的交点为M,![]() .
.
(1)求椭圆的方程;
(2)过点M的直线![]() 与椭圆交于C、D两点,若
与椭圆交于C、D两点,若![]() ,求直线
,求直线![]() 的方程;
的方程;
(3)若点P为准线![]() 上的动点,求∠F1PF2最大值.
上的动点,求∠F1PF2最大值.
 |
参考答案
一、 选择题
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | B | A | B | C | D | C | C | C | C | C |
二、 填空题
11. 2 12. -1/4
13. 0 14. 3,4
三、 解答题
15.(1)![]()
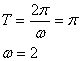 ------------------------------2分
------------------------------2分
![]() -------------------------------5分
-------------------------------5分
因为![]() 所以:非奇非偶--------------------------------2分
所以:非奇非偶--------------------------------2分
 |
(2)(略)
16.方法一:
(1)![]()
![]() ,
,
∴ ![]() ,
,![]() ,
,
![]()
![]() ,
,
∴ ![]() 平面
平面![]() .
……………………3分
.
……………………3分
(2)当M为PC中点时,即![]() 时,直线
时,直线![]() 平面
平面![]() , …………4分
, …………4分
证明如下:
由(Ⅰ)知![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,∴
,∴ ![]() , ……5分
, ……5分
在等腰![]() 中,
中,![]() M为
M为![]() 中点,∴
中点,∴ ![]() ,
…………6分
,
…………6分
又![]() ,
,
∴ ![]() 平面
平面![]() .
……………8分
.
……………8分
(3)由(Ⅱ)知当M为PC中点时,![]() 平面
平面![]() ,
,![]()
![]() 平面
平面![]() ,
,
∴ 平面![]() 平面
平面![]() .
……………………9分
.
……………………9分
过![]() 作
作![]() 于
于![]() ,∴
,∴ ![]() 平面
平面![]()
作![]() 于
于![]() ,连结
,连结![]() ,由三垂线定理可知,
,由三垂线定理可知,![]() .
.
∴ ![]() 为二面角
为二面角![]() 的平面角.
……………………11分
的平面角.
……………………11分
设![]() ,则
,则![]() .
.
在![]() 中,
中,![]() ,
,
由(Ⅰ)知![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,∴
,∴ ![]() .
.
在![]() 中,
中,![]()
![]() .
.
由面积公式得![]() ,
,![]() ,
……………12分
,
……………12分
同理,在![]() 中,
中,![]() 由面积公式得
由面积公式得![]() , ……………13分
, ……………13分
在![]() 中,
中,![]() .
.
所以二面角![]() 的大小为
的大小为![]() . ……………………14分
. ……………………14分
17.(Ⅰ)由题意![]() ,
,
∴![]() .
…………………………………………………………………2分
.
…………………………………………………………………2分
当![]() 时,
时,![]() =
=![]() , …………………5分
, …………………5分
又当![]() 时,
时,![]() ,适合上式,
,适合上式,
∴![]() . …………………………………………………………………7分
. …………………………………………………………………7分
(Ⅱ)∵ ![]() ,
,
∴ 数列![]() 是首项为1,公差为
是首项为1,公差为![]() 的等差数列,…………………………………9分
的等差数列,…………………………………9分
其前![]() 项和为
项和为![]() ,故
,故![]() ,……………………………11分
,……………………………11分
![]() ,得
,得![]() ,
,
满足它的最小整数是![]() ,即此数列最少有
,即此数列最少有![]() 项. …………………………………14分
项. …………………………………14分
18.
(Ⅰ)前4辆恰有2辆左转行驶的概率![]() ……7分
……7分
(Ⅱ)该车在第一次绿灯亮起时的1分钟内通过该路口的概率
![]() ………………14分
………………14分
19.1)![]() -------------2分
-------------2分
因![]() 取得极值,所以
取得极值,所以
![]()
|
|
(2)![]()
![]()
|
当![]()
![]() 所以
所以![]() 上为增函数,从而f(x)在
上为增函数,从而f(x)在![]() 上也为增函数。------------------------------13分
上也为增函数。------------------------------13分
综上所述,当![]() 上为增函数。 ----------14分
上为增函数。 ----------14分
20.(1)设椭圆方程为![]() ,半焦距为
,半焦距为![]() ,
,
则![]()
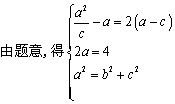
![]()
![]() ………………………………………………4分
………………………………………………4分
(2) 点M的坐标为![]() ,设C、D两点的坐标分别为
,设C、D两点的坐标分别为![]() ,
,
![]() 的方程为
的方程为![]() ,代入椭圆方程并整理得:
,代入椭圆方程并整理得:
![]() ①
①
则![]() ②-----------------------------6分
②-----------------------------6分
由 ![]() 得:
得:![]() ,
③-------------------------------7分
,
③-------------------------------7分
又![]() ,
④-
,
④-
由②③④得:![]() ,……………………8分
,……………………8分
解得:![]() ,代入①有检验有
,代入①有检验有![]() ,
,![]()
得所求直线![]() 的方程为
的方程为![]() ………………………………………10分
………………………………………10分
(3)![]()