高考数学试题赏析

高考数学试题赏析

以下是07年高考湖卷北理科第10题：

已知直线（a,b是非零常数）与圆x²+y²=100有公共点，且公共点的横坐标和纵坐标均为整数，那么这样的直线共有　　　　　　　　　　　　　　　　 　（　　　　　）

A.60条　　　　　　　  B.66条　　　　　　  C.72条　　　　　　　 D.78条

对于这道题，山里人——汪跃中老师提出如

下“猜”法：

　　 一猜圆上有几个整点.

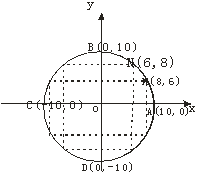
如图，我们称横坐标和纵坐标均为整数为整

点.圆上的整点都是x²+y²=100的整数解.由勾股

定理知这些点分别是：（10，0），（8，6），（6，8），

（0，10），（-6，8），（-8，6），（-10，0），…，

（8，-6）共12个点.

二猜过圆上一个整点的切线有多少？——12条.

 三猜过圆上两个整点的直线（即割线）有多少？

——条.

以上共计12+66=78条.

四猜原题有什么陷阱，即以上这些直线中有哪些不合条件？

由于是直线的截距式，要求其纵、横截距均不为零，故在上述直线中，以下直线不合条件：

（1）　　　 过原点的直线，也就是圆的直径所在直线，有6条；

（2）　　　 与坐标轴平行的割线，有8条；

（3）　　　 与坐标轴平行的切线，有4条.

以上共计18条.

因此，符合条件的直线共有78-18=60条，故选A.

汪跃中老师最后说：

本题涉及的基础知识，数的方面有：圆的方程、截距不为零的直线方程、勾股数、组合数等；形的方面有：整点、过圆上一个整点的切线、过圆上两个整点的直线、去掉过原点的直线、平行于坐标轴的直线等.

解本题的基本功体现在综合分析本题涉及的数与形的特点及其运用的能力上.

因为本题虽然涉及的知识面广，但什么样的考生都能动手，但要不犯一点错误却是很不容易的，题不难而区分度高，所以我们认为本题是一道难得的好题.