高考数学文科预测卷
命题人:关剑 审题人:徐启明
1.已知集合![]() ,集合
,集合![]() ,则( )
,则( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2、已知函数![]() 则下列判断正确的是
则下列判断正确的是
A此函数的最小正周期为![]() ,其图象的一个对称中心是
,其图象的一个对称中心是![]()
B此函数的最小正周期为![]() ,其图象的一个对称中心是
,其图象的一个对称中心是![]()
C此函数的最小正周期为![]() ,其图象的一个对称中心是
,其图象的一个对称中心是![]()
D此函数的最小正周期为![]() ,其图象的一个对称中心是
,其图象的一个对称中心是![]()
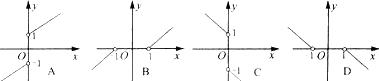
3.函数y=![]() +x的反函数图像是( )
+x的反函数图像是( )
4.直线![]() 相切,则直线l的一个方向量
相切,则直线l的一个方向量![]() =
=
A.(2,-2) B.(1,1) C.(-3,2) D.(1,![]() )
)
5.设x,y满足约束条件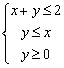 ,则z=3x+y的最大值是
,则z=3x+y的最大值是
A. 0 B. 4 C. 5 D. 6
6.设l,m,n是空间三条直线,![]() ,
,![]() 是空间两个平面,则下列选项中正确的是( )
是空间两个平面,则下列选项中正确的是( )
(A) 当n⊥![]() 时,“n⊥
时,“n⊥![]() ”是“
”是“![]() ∥
∥![]() ”成立的充要条件
”成立的充要条件
(B) 当m Ì a且n是l在![]() 内的射影时,“m⊥n,”是“l⊥m”的充分不必要条件
内的射影时,“m⊥n,”是“l⊥m”的充分不必要条件
(C) 当m Ì a时,“m⊥![]() ”是“
”是“![]() ”必要不充分条件
”必要不充分条件
(D) 当m Ì a,且n Ë a时,“n∥![]() ”是“m∥l”的既不充分也不必要条件
”是“m∥l”的既不充分也不必要条件
7.若双曲线![]() 的两条渐近线恰好是抛物线
的两条渐近线恰好是抛物线![]() 的两条切线,则a的值为
( )A.
的两条切线,则a的值为
( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.已知正方体ABCD-![]() 的棱长为1,对于下列结论:
的棱长为1,对于下列结论: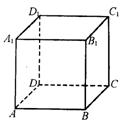
①BD![]() ⊥平面A
⊥平面A![]() DC
DC![]() ;②A
;②A![]() C
C![]() 和AD
和AD![]() 所成角为45°;③点A与点C
所成角为45°;③点A与点C![]() 在该正方体外接球表面上的球面距离为
在该正方体外接球表面上的球面距离为![]() .其中正确结论的个数是
.其中正确结论的个数是
A.0 B.1 C.2 D.3
9.要从10名男生与5名女生中选出6名学生组成课外活动小组,如果按性别分层抽样,试问组成此课外活动小组的概率为 ( )
A.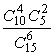 B.
B.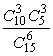 C.
C.![]() D.
D.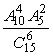
10.在![]() 中,
中,![]() ,
,![]() ,
,![]() .则
.则![]() 的值为( )
的值为( )
A.![]() B.
B.![]()
|
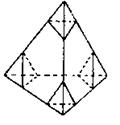
11.将棱长为3的正四面体以各顶点截去四个棱长为1的小正四面体(使截面平行于底面),所得几何体的表面积为( )
A.![]() B.
B. ![]() C
C ![]() D.
D.
![]()
12.设 f (x)=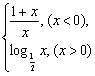 ,则f
(x)≥
,则f
(x)≥![]() 的解集是( )
的解集是( )
A.(-∞,-2![]() ∪
∪![]()
![]() , +∞)
B.
, +∞)
B. ![]() -2, 0)∪(0,
-2, 0)∪(0,
![]()
![]()
C. ![]() -2, 0)∪
-2, 0)∪![]()
![]() , +∞)
D. (-∞,-2
, +∞)
D. (-∞,-2![]() ∪(0,
∪(0, ![]()
![]()
13.已知函数![]() 满足
满足![]() ,则
,则![]()
14.若![]() 的展开式中的第五项是
的展开式中的第五项是![]() , Sn=
, Sn=
15.过椭圆的左焦点F且倾斜角为60°的直线交椭圆于A,B两点,若![]() ,则椭圆的离心率e=
。
,则椭圆的离心率e=
。
16、若两个向量![]() 与
与![]() 的夹角为q,则称向量“
的夹角为q,则称向量“![]() ×
×![]() ”为“向量积”,其长度
”为“向量积”,其长度![]() ×
×![]() =
=![]() •
•![]() •sinq。今已知
•sinq。今已知![]() =1,
=1,![]() =5,
=5,![]() •
•![]() =-4,则
=-4,则![]() ×
×![]() = 。
= 。
17.(12分)已知向量![]() ,定义函数
,定义函数![]() .
.
(1)求![]() 的最小正周期和最大值及相应的x值;(10分)
的最小正周期和最大值及相应的x值;(10分)
(2)当![]() 时,求x的值.(2分)
时,求x的值.(2分)
18. (12分)甲、乙、丙三个口袋内都分别装有6个不相同的球,并且每个口袋内的6个球均有1个红球,2个黑球,3个无色透明的球,现从甲、乙、丙三个口袋中依次随机各摸出1个球.求:(1)求恰好摸出红球、黑球和无色球各1个的概率;
(2)求摸出的3个球中含有有色球不少于2个的概率。
|
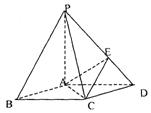
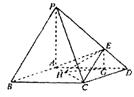
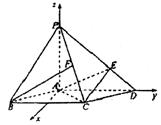
(2)求以AC为棱, EAC与DAC为面的二面角θ的大小;
(3)在棱PC上是否存在一点F,使BE//平面AEC?证明你的结论。
20.已知各项均为正数的数列{an}的前n项和为Sn,首项为a1,且![]() 成等差数列。(1)求数列{an}的通项公式;(2)若
成等差数列。(1)求数列{an}的通项公式;(2)若![]()
21 已知函数![]() 的导数的f′(x),若曲线y= f(x)上两点A、B处的切线都与x轴平行,且直线AB的斜率小于
的导数的f′(x),若曲线y= f(x)上两点A、B处的切线都与x轴平行,且直线AB的斜率小于![]() 时,
时,
f′(x)-3x2≤2恒成立,求a的取值范围.
22.本大题满分(14分)
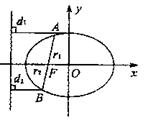
![]() 已知定点
已知定点![]() ,动点
,动点![]() 在
在![]() 轴上运动,过点
轴上运动,过点![]() 作
作![]() 交
交![]() 轴于点
轴于点![]() ,并延长
,并延长![]() 到点
到点![]() ,且
,且![]() ,
,![]() .
.
(1)求动点![]() 的轨迹方程;(2)直线
的轨迹方程;(2)直线![]() 与动点
与动点![]() 的轨迹交于
的轨迹交于![]() 、
、![]() 两点,若
两点,若![]() ,且
,且![]() ,求直线
,求直线![]() 的斜率
的斜率![]() 的取值范围.
的取值范围.
高考数学文科预测卷答案
1.B 2.B 3. B.
4.解答. A ![]() ,
,
直线![]() ,
,![]() ,因此,选择A.
,因此,选择A.
5.D 6.A
7.解答B.双曲线![]() 的两条渐近线为
的两条渐近线为![]() ,它恰好是抛物线
,它恰好是抛物线![]()
的两条切线,![]() ,且
,且![]() ,故选B.
,故选B.
8.C.由三垂线定理易证BD1⊥A1D,BD1⊥A1C1;②中夹角应为60°;正方体外接球半径为![]() ,点A与点C1的球面距离恰为大圆周长的一半,即
,点A与点C1的球面距离恰为大圆周长的一半,即![]() π.故①③正确.
π.故①③正确.
9.解答 A 从10名男生、5名女生中选出6名的不同选法只有C![]() 种;按分层抽样,设抽男生x人,女生y人,有
种;按分层抽样,设抽男生x人,女生y人,有![]() 则组成此课外活动小组需抽取4名男生、2名女生,不同选法有C
则组成此课外活动小组需抽取4名男生、2名女生,不同选法有C![]() ·C
·C![]() 种,∴P=
种,∴P=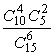 .因此选择A.
.因此选择A.
10.解答B. 由余弦定理:![]() 得:
得:![]() ,
,
|
所以,![]()
![]()
![]() . 即
. 即![]() .
.
11.原正四面体的表面积为![]() ,每截去一个小正四面体,
,每截去一个小正四面体,
表面减少三个小正三角形,增加一个正三角形,故表面积减少
![]() ,故所得几何体的表面积为
,故所得几何体的表面积为![]() .选择A
.选择A
12.D
13.1
14. 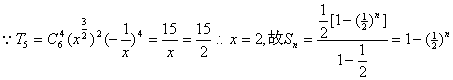
|
![]() 注意到直线AB的倾斜角为60°
注意到直线AB的倾斜角为60°
![]()
16.3
17.解:(1)![]() --------------------2分
--------------------2分
![]() --------------------4分
--------------------4分
![]() --------------------6分
--------------------6分
![]()
![]() .--------------------8分
.--------------------8分
当![]() 时(9分),
时(9分),![]() 取最大值
取最大值![]() .--------------------10分
.--------------------10分
(2)当![]() 时,
时,![]() ,即
,即![]() ,--------------------11分
,--------------------11分
解得![]() ,
,![]() .-------------------- 12分
.-------------------- 12分
18.解:(1)P1=![]() ×
×![]() ×
×![]() ×
×![]() =
=![]() .--------------------6
.--------------------6
(2)(文科)P2=![]() (
(![]() +
+![]() )2(
)2(![]() )+
)+![]() (
(![]() +
+![]() )3=
)3=![]() ------------------11
------------------11
答:----------12
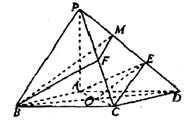
19.证明:因为底面ABCD是菱形,∠ABC=60°,所以AB=AD=AC=a,在△PAB中,
由PA2+AB2=2a2=PB2 知PA⊥AB.
同理,PA⊥AD,所以PA⊥平面ABCD.(3分)
|
由PA⊥平面ABCD.
知EG⊥平面ABCD.作GH⊥AC于H,连结EH,
则EH⊥AC,∠EHG即为二面角θ的平面角.
又PE:ED=2:1,
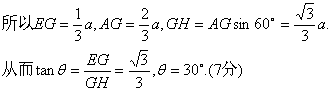
|
A(0,0,0),B(![]() a,-
a,-![]() a,0),C(
a,0),C(![]() a,
a, ![]() a,0).
a,0).
D(0,a,0),P(0,0,a),![]() .
.
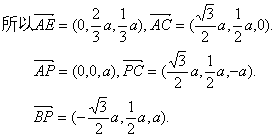
设点F是棱PC上的点,![]() ,则
,则
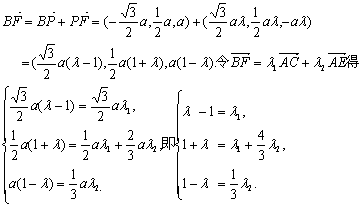 、
、
![]()
亦即,F是PC的中点时,![]() 、
、![]() 、
、![]() 共面.
共面.
又BF![]() 平面AEC,所以当F是棱PC的中点时,BF//平面AEC.(12分)
平面AEC,所以当F是棱PC的中点时,BF//平面AEC.(12分)
解法二 当F是棱PC的中点时,BF//平面AEC,证明如下,
|
由![]() ,知E是MD的中点.
,知E是MD的中点.
连结BM、BD,设BD∩AC=O,则O为BD的中点.
所以BM//OE. ②
由①、②知,平面BFM//平面AEC 。
又BF![]() 平面BFM,所以BF//平面AEC.
平面BFM,所以BF//平面AEC.
证法二:
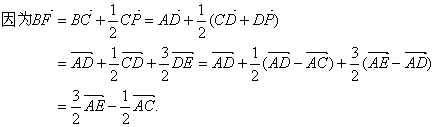
所以![]() 、
、![]() 、
、![]() 共面.
共面.
又BF![]() 平面ABC,从而BF//平面AEC.
平面ABC,从而BF//平面AEC.
20.(文)解(1)由题意知![]()
当n=1时,![]()
当![]()
两式相减得![]()
整理得:![]() ……………………………………………………4分
……………………………………………………4分
∴数列{an}是![]() 为首项,2为公比的等比数列.
为首项,2为公比的等比数列.
![]() ……………………………………5分
……………………………………5分
(2)![]()
![]() …………………………………………………………6分
…………………………………………………………6分
![]()
![]() ①
①
![]() ②
②
①-②得![]() ………………9分
………………9分
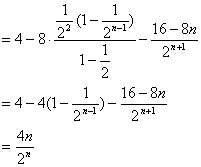 …………………………11分
…………………………11分
![]() …………………………………………………………12分
…………………………………………………………12分
21(文)解:![]()

22解:(1)设![]() ,
,![]()
![]()
![]()
![]()
![]() 为
为![]() 的中点,
的中点,![]()
![]() ………………(1分)
………………(1分)
![]() 在
在![]() 轴上,
轴上,![]()
![]() 即为
即为![]()
![]()
![]()
![]() ,
,![]()
![]()
![]() ,
,![]() 又
又![]() 即
即![]()
![]()
![]()
故点![]() 的轨迹方程为
的轨迹方程为![]() ……………………(6分)
……………………(6分)
(2)![]() 恰为
恰为![]() 的焦点,设
的焦点,设![]() 为:
为:![]() 代入
代入![]()
得:![]()
设![]() ,
,![]() 即
即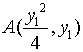 ,
,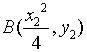
![]()
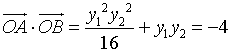
![]()
![]()
![]()
![]() 又
又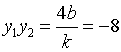
![]()
![]() …………………………………………(10分)
…………………………………………(10分)
即 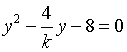 又
又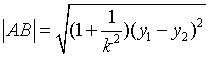
![]()
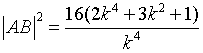
![]()
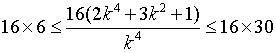
解之得 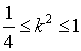
![]()
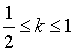 或
或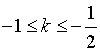 ………………14分
………………14分