高考数学综合训练(四)
一、选择题
1.已知集合![]() ,
,![]() ,那么集合
,那么集合![]() 等于
等于
A.![]() B.
B.![]()
C.![]() D.
D.![]()
2.将函数![]() 的图像按向量
的图像按向量![]() 平移后,得到
平移后,得到![]() 的图像,则
的图像,则
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.在空间中,有如下四个命题:
①平行于同一个平面的两条直线是平行直线,
②垂直于同一条直线的两个平面是平行平面;
③若平面![]() 内有不共线的三个点到平面
内有不共线的三个点到平面![]() 距离相等,则
距离相等,则![]() //
//![]() ;
;
④过平面![]() 的一条斜线有且只有一个平面与平面
的一条斜线有且只有一个平面与平面![]() 垂直。
垂直。
其中正确的两个命题是
A.①、③ B.②、④ C.①、④ D.②、③
4.若![]() ,其中a、b
,其中a、b![]() 是虚数单位,则
是虚数单位,则![]() 等于( )
等于( )
A.-3 B.-1 C.3 D.1
5、先将一个棱长为3的正方体木块的六个面分别涂上六种颜色,再将该正方体均匀割成棱长为1的小正方体,现从切好的小正方体中任取一块,所得正方体的六个面均没有涂色的概率是( ).
A.![]() B.
B.![]() C.
C. ![]() D.
D. ![]()
6.在函数![]() 在
在![]() 上是增函数,则
上是增函数,则![]() 的值可以是
的值可以是
A.1 B.2 C.-1 D.-2
7. 若样本![]() ,
,![]() ,…,
,…,![]() 的平均数为1,方差为2,则样本
的平均数为1,方差为2,则样本![]() ,
,![]() ,…,
,…,![]() 的平均数和方差分别为( )
的平均数和方差分别为( )
A.平均数为3,方差18 B.平均数为2,方差17
C.平均数为2,方差18 D.平均数为3,方差17
8、设椭圆的两个焦点分别为F1、F2,过F2作椭圆长轴的垂线与椭圆相交,其中的一个交点为P,若△F1PF2为等腰直角三角形,则椭圆的离心率是( ).![]()
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
9、已知数列![]() 的各项均为正数,其前
的各项均为正数,其前![]() 项和为
项和为![]() ,若
,若![]() 是公差为-1的等差数列,且
是公差为-1的等差数列,且![]() ,那么
,那么![]() 的值是( )
的值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.设![]() ,则对任意实数
,则对任意实数![]() 、
、![]() ,“
,“![]() ”,是“
”,是“![]() ”的( )
”的( )
A.充要条件 B.充分而不必要条件 C.必要而不充分条件D.既不充分又不必要条件
二.填空题(本大题共6小题,每小题5分,共30分,把答案填在题中横线上。)
11.在平面直角坐标系中,不等式组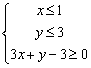 所表示的平面区域的面积是________。
所表示的平面区域的面积是________。
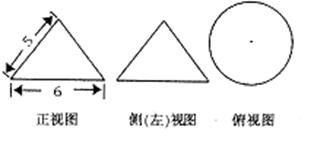 12.一个几何体的三视图及其尺寸如下(单位:㎝),则该几何体的表面积是
,体积是
.
12.一个几何体的三视图及其尺寸如下(单位:㎝),则该几何体的表面积是
,体积是
.
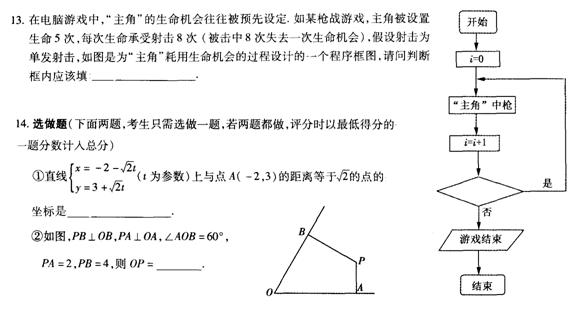 三.解答题(本大题共6小题,共80分,解答应写出文字说明,证明过程或演算步骤。)
三.解答题(本大题共6小题,共80分,解答应写出文字说明,证明过程或演算步骤。)
15.(本小题满分12分)已知![]() 是等差数列,
是等差数列,![]()
(Ⅰ)求![]() 的通项公式;(Ⅱ)设
的通项公式;(Ⅱ)设![]() 的前
的前![]() 项和
项和![]() ,求
,求![]() 的值
的值
16.(本小题满分12分)已知函数![]()
(Ⅰ)求![]() 的定义域; (Ⅱ)设
的定义域; (Ⅱ)设![]() 是锐角,且
是锐角,且![]() ,求
,求![]() 的值。
的值。
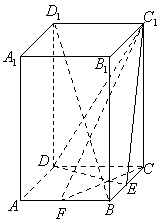
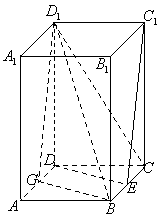
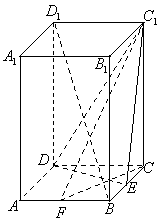 17.(本小题满分14分)如图,
17.(本小题满分14分)如图,![]() 是正四棱柱,侧棱长为3,底面边长
是正四棱柱,侧棱长为3,底面边长
为2,![]() 、
、![]() 是分别是
是分别是![]() ,
,![]() 的中点。
的中点。
(Ⅰ)求证:![]() //平面
//平面![]() ;
;
(Ⅱ)求异面直线![]() 和
和![]() 所成角的余弦值;
所成角的余弦值;
(Ⅲ)求证:平面![]() 平面
平面![]() 。
。
18.(本小题满分14分)经过长期观测得到:在交通繁忙的时间段内,某段公路汽车的车流量y(千辆/小时)与汽车的平均速度v(千米/小时)之间的函数关系为![]() .
.
(Ⅰ)在该时段内,当汽车的平均速度v为多少时,车流量最大?最大车流量为多少?
(Ⅱ)若要求在该时段内车流量超过9千辆/小时,则汽车的平均速度应在什么范围内?

20.(本小题满分14分)已知函数![]() 在
在![]() 处取得极值2.
处取得极值2.
(1)求函数![]() 的解析式;
的解析式;
(2) ![]() 满足什么条件时,区间(
满足什么条件时,区间(![]() ,2
,2![]() +1)为函数
+1)为函数![]() 的单调增区间;
的单调增区间;
(3)若![]() 为
为![]() 图象上任意一点,直线
图象上任意一点,直线![]() 与
与![]() 的图象切于
的图象切于![]() 点,求直线
点,求直线![]() 的斜率的取值范围.
的斜率的取值范围.
高考数学综合训练(四)(四)
班级 姓名 座号
一、选择题:
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
|
|
|
|
|
|
|
|
|
|
二、填空题:
11、 12、 、 13、
14(1) (2)
三、解答题:
15、
16、
 17、
17、
18、
高考数学综合训练(四)
参考答案
一、选择题:
1.D 2.C 3.B 4.D 5.D 6.A 7.C 8.D 9.A 10.A
二、填空题:
11.![]() 12.
12.![]() ,
,![]() 13.
13.![]() 。14、(1)
。14、(1)![]() 或
或![]() (2)
(2)![]()
三、解答题:本大题共6小题,共80分,解答应写出文字说明,证明过程或演算步骤。
15.(Ⅰ)解:设等差数列![]() 的公差为
的公差为![]() ,
,
则![]() 2分
2分
解得![]() ,
,![]() 4分
4分
所以数列![]() 的通项为
的通项为![]() 6分
6分
(Ⅱ)解:数列![]() 的前
的前![]() 项和为
项和为![]() 9分
9分
由![]() 化简得
化简得![]() ,
,
即![]() 所以
所以![]() 12分
12分
16.(Ⅰ)解:由![]() 得
得![]() 1分
1分
得![]() (
(![]() ) 3分
) 3分
所以![]() 的定义域为
的定义域为![]() 5分
5分
(Ⅱ)解:因为![]() 是锐角,且
是锐角,且![]() 7分
7分
![]()
![]() 9分
9分
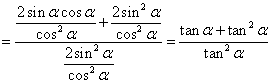 (12分)
(12分)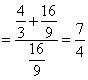 故
故![]() (14分)
(14分)
![]()
![]()
17.(Ⅰ)证明:连接![]() ,与
,与![]() 相交于
相交于![]() ,连接
,连接![]()
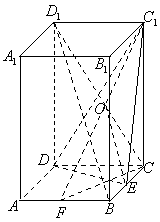
∵![]() 是矩形
是矩形
∴![]() 是
是![]() 的重点,又
的重点,又![]() 是
是![]() 的中点
的中点
∴![]() 又
又![]() 平面
平面![]() ,
,![]() 平面
平面![]()
∴![]() 平面
平面![]() 4分
4分
 (Ⅱ)取
(Ⅱ)取![]() 中点
中点![]() ,连结
,连结![]() ,
,![]() ,
,
∵![]() ,
,![]()
∴四边形![]() 是平行四边形∴
是平行四边形∴![]()
故![]() 就是异面直线
就是异面直线![]() 和
和![]() 所成角
所成角
在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]()
∴异面直线![]() 和
和![]() 所成角的余弦值为
所成角的余弦值为![]()
(Ⅲ)∵![]() ,∴
,∴![]() ,
,
又
∵![]() ∴
∴![]() ∴
∴![]()
又
∵![]() 平面
平面![]() ,
,![]() 平面
平面![]()
![]() ,
,![]()
∴![]() 平面
平面![]() 而
而 ![]() 平面
平面![]() ∴平面
∴平面![]() 平面
平面![]()
18、(1)解: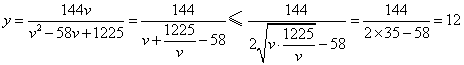
当且仅当![]() 即
即![]() 时,上式取等于号,
时,上式取等于号,
即当汽车的平均速度为![]() 千米/小时,车流量最大,最大车流量为
千米/小时,车流量最大,最大车流量为![]() 千辆/小时,
千辆/小时,
(2)由![]() 得
得 ![]()
![]() ,故上式等价于
,故上式等价于![]()
![]() 解得
解得![]()
车流量超过9千辆/小时,则汽车的平均速度应在![]()

20、解:(1)![]() ∴
∴![]() 。
。
∴![]() 。
。
(2)![]() ,令
,令![]() 。
。
∴![]()
所以只需![]() 是其子区间即可。
是其子区间即可。
∴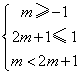
(3)设直线![]() 的斜率为
的斜率为![]() ,则
,则![]()
即![]()
其值域为直线的斜率![]() 的范围。
的范围。
令![]() 即
即![]() ,
,
![]()
∴![]()