高三数学第二轮复习教学案
第十五课时 求定性曲线的标准方程及求动点的轨迹方程
班级 学号 姓名
【考纲解读】
1.理解求曲线方程的一般步骤.
2.掌握求动点的轨迹方程时常见的基本方法.
【教学目标】
1.使学生会求曲线的标准方程(求基本量)和动点的轨迹方程.
2.进一步培养学生逻辑推理能力、运算能力、分析问题和解决问题的能力.
【例题讲解】
例题1
（1）圆心在抛物线
上，并且与抛物线的准线及
轴都相切的圆的方程是（ ）
A 
B 
C 
D 
（2）已知椭圆
=1和双曲线
有公共的焦点，那么双曲线的渐近线方程是（ ）
A 
B 
C 
D 
（3）已知两点
给出下列曲线方程：①
；②
；③
；④
，在曲线上存在点P满足
的所有曲线方程是（ ）
A ①③ B ②④ C ①②③ D ②③④
（4）已知两点
，动点
在
轴上的射影为
，则动点P的轨迹方程为_________.
(5)已知直线
交椭圆
于
两点，椭圆与轴的正半轴交于B点，若
的重心恰好落在椭圆的右焦点上，则直线的方程是_________.
(6)已知曲线
及直线
，曲线
与
关于直线对称，则曲线的方程为________.
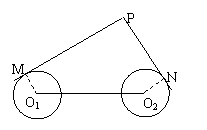例2如图，圆
和圆
的半径都等于1，
=4，过动点P分别作圆、圆的切线
为切点），使得
，试建立平面直角坐标系，并求动点P的轨迹方程.
例3 一个椭圆中心在原点，焦点
、
在轴上，P（
）是椭圆上一点，且
成等差数列，求椭圆的方程.
例4如图，过点A（
，斜率为
的直线与抛物线
交于P、
两点，（1）若曲线C的焦点F与P、、R三点按如图顺序成平行四边形
，求点R
的轨迹方程.
（2）设、两点只在第一象限运动，点（0，8）与线段
中点的连线交轴于点N，当点N在A点右侧时，求的取值范围.
 |
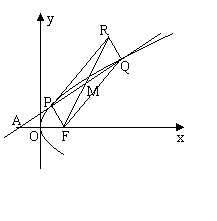例5点
是椭圆
上的一点，、、
分别为关于轴、原点、轴的对称点，
为椭圆上异于的另一点，且
，
与
的交点为
，当沿椭圆运动时，求动点的轨迹方程.
高三数学第二轮复习教学案
第十六课时 定义法与几何法及函数、方程、不等式法研究曲线性质
班级 学号 姓名
【考纲解读】
1.通过方程研究性质是解析几何的一个基本问题.
2.理解能用函数、方程、不等式等方法研究曲线的性质.
【教学目标】
1. 夯实基础知识，灵活运用基本方法解决问题.
2. 进一步发挥解几问题中几何方法与代数方法的互补作用.
【例题讲解】
例题1
（1）若
表示圆，则
的取值范围为（ ）
A 
B 
C 
D 
（2）设P是椭圆
上一动点，
是椭圆的两个焦点，则
的最小值是（ ）
A 
B 
C 
D 
（3）已知双曲线
，则过P(2,1)且与双曲线有且只有一个公共点的直线有（ ）条
A 1 B 2 C 3 D 4
（4）设双曲线
中，离心率
，则两条渐近线的夹角
的取值范围是_________.
（5）抛物线
上离点
最近的点恰好是顶点，则
的取值范围是______.
（6）点
在椭圆
的左准线上，过点P且方向为
的光线经直线
反射后通过椭圆的左焦点，则这个椭圆的离心率为__________.
例2设
两点在抛物线
上，是AB的垂直平分线，当直线的斜率为2时，求在轴上截距的取值范围.
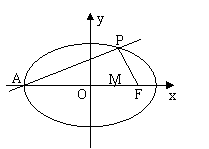
例3如图，点A、B分别是椭圆
的长轴的左右端点，点
是椭圆的右焦点，点在椭圆上，且位于轴上方，
.
(1) 求点P的坐标.
(2)设是椭圆长轴
上一点，到直线
的距离等于
，求椭圆上点到点的距离
的最小值.
 |
例4已知双曲线的右焦点为，过点作直线
垂直于该双曲线的一条渐近线
于P
（1）求该双曲线的方程.
（2）过点作直线
交该双曲线于、两点，如果
，求直线的方程.
例5给定抛物线，是的焦点，过点的直线与相交于A，B两点，设
，若
，求在轴上的截距的变化范围.