三角函数的性质
1.已知
，
，则
的取值范围是（
）
A、＜－1 B、
C、＞3 D、
或＜－1
2.当
时，函数
的值域是（
）
A、[－1, 1] B、
，1] C、[－2,
2] D、[－1, 2]
3.若
，则
的最大值和最小值分别是（ ）
A、7, 5 B、7，
C、5， D、7，－5
4.函数
是（
）
A、奇函数 B、偶函数 C、非奇非偶函数 D、以上都不是
5.函数y＝sin(2x＋
)的最小正周期是（
）
(A) 
(B) 
(C)
2 (D)4
6.下列函数中，既是区间
上的增函数，又是以为周期的偶函数的是（
）
A、
B、
C、
D、
7.函数f (x) = sin x +cos x 的最小正周期是 （ ）
(A)
(B)
（C）
（D）2
8.函数
在下列哪个区间上是减函数（
）
A．
B．
C． 
D．
9.已知函数y =tan 
在（－
，）内是减函数，则（ ）
A. 0 <
≤ 1 B.－1 ≤< 0
C. ≥ 1
D. ≤ －13、
10. 函数
是（
）
A、非奇非偶函数 B、仅有最小值的奇函数
C、仅有最大值的偶函数 D、既有最大值又有最小值的偶函数
11.已知函数
的最大值为
，最小值为
，则
＿＿，
＿＿＿。
12.函数
是奇函数，则
的值为 .
13.函数
的递减区间是
；函数
的递减区间是
.
14.函数
的最小正周期T=__________.
15.若
是以
为周期的奇函数，且
，则
＝ .
16.已知函数
为常数），且
，则
.
17. 已知函数
。
（1）求的最小正周期； （2）求的单调区间；
（3）求图象的对称轴和对称中心。
18. 已知函数
。
（1）求
的最小正周期； （2）若
，求的值域。
19.化简
，并求函数的值域和最小正周期．
20.已知函数
。
（1）求的最小正周期；
（2）求的最小值及取得最小值时相应的
值；
（3）若
，求满足
的值。
21. 求函数
的最值。
第四章复习6 三角函数的性质参考答案
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | C | D | D | B | B | B | C | C | B | D |
11. 
；1. 12.
13. 
14. 
15. －1 16.
－5
17、（1） （2）递增区间为
，递减区间为
（3）对称轴
，对称中心
18. （1） （2）
19．解：
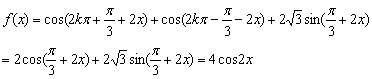
函数f(x)的值域为
; 函数f(x)的周期
；
20、(1) (2)2；
（3）
21、当
时，
，
；当
时，
，；当
时，，
；当
时，
，