三角函数
一.最值问题
1.函数![]() 的最小值是 .
的最小值是 .
2.函数![]() 的最小值是
.
的最小值是
.
3.函数y=sinxcosx+sinx+cosx的最大值是 .
4.当-![]() ≤x≤
≤x≤![]() 时, 函数f (x)=sinx+
时, 函数f (x)=sinx+![]() cosx的( )。
cosx的( )。
A.最大值是2,最小值是-2 B.最大值是1,最小值是-![]()
C.最大值是1,最小值是-1 D.最大值是2,最小值是-1
5. 已知k<-4,则函数y=cos2x+k(cosx-1)的最小值是( )
A. 1 B. -1 C. 2k+1 D. -2k+1
6.函数![]() 在区间
在区间![]() 上的最小值是(
)
上的最小值是(
)
A.![]() B.
B.![]() C.-1 D.
C.-1 D.![]()
7.设![]() ,对于函数
,对于函数![]() ,下列结论正确的是( )
,下列结论正确的是( )
A.有最大值而无最小值 B.有最小值而无最大值
C.有最大值且有最小值 D.既无最大值又无最小值
8.当![]() 时,函数
时,函数![]() 的最小值为(
)
的最小值为(
)
A.2 B.![]() C.4 D.
C.4 D.![]()
9.设实数![]() 满足
满足![]() ,
,![]() 是正常数,且
是正常数,且![]() ,那么
,那么![]() 的最大值是
( )
的最大值是
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.已知a>0, 0≤x<2π,函数y=cos2x-asinx+b的最大值为0,最小值为-4,试求a和b的值,并求出使y取得最大值和最小值时的x的值。
11.设函数![]() (其中
(其中![]() >0,
>0,![]() ),且f(x)的图象在y轴右侧的第一个最高点的横坐标为
),且f(x)的图象在y轴右侧的第一个最高点的横坐标为![]() .
.
(1)求ω的值;(2)如果f(x)在区间![]() 上的最小值为
上的最小值为![]() ,求a的值.
,求a的值.
二.三角形中的三角函数
1. 在△![]() 中,已知
中,已知![]() ,三角形面积为12,则
,三角形面积为12,则![]() .
.
2. 在![]() 中,已知
中,已知![]() ,则
,则![]() = .
= .
3.在![]() 中,A>B是
中,A>B是![]() 成立的 条件.
成立的 条件.
4.在![]() 中,若
中,若![]() ,则
,则![]() 的形状为 .
的形状为 .
5.在![]() 中,
中,![]() 分别是角A、B、C所对的边,若
分别是角A、B、C所对的边,若![]()
![]() ,则
,则![]() = .
= .
6.若△![]() 的内角
的内角![]() 满足
满足![]() ,则
,则![]() =( )
=( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D.
![]()
7.在![]() 中,若
中,若![]() ,则
,则![]() 必定是( )
必定是( )
A.钝角三角形 B.锐角三角形 C.直角三角形 D.等腰三角形
8.在△OAB中,O为坐标原点,![]() ,则当△OAB的面积达最大值时,
,则当△OAB的面积达最大值时,![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9.在![]() 中,已知
中,已知![]() ,给出以下四个论断其中正确的是( )
,给出以下四个论断其中正确的是( )
① ![]() ②
② ![]()
③ ![]() ④
④ ![]()
A.①③ B.②④ C.①④ D.②③
10.如果![]() 的三个内角的余弦值分别等于
的三个内角的余弦值分别等于![]() 的三个内角的正弦值,则( )
的三个内角的正弦值,则( )
A.![]() 和
和![]() 都是锐角△ B.
都是锐角△ B.![]() 和
和![]() 都是钝角△
都是钝角△
C.![]() 是钝角三角形,
是钝角三角形,![]() 是锐角三角形
是锐角三角形
D.![]() 是锐角三角形,
是锐角三角形,![]() 是钝角三角形
是钝角三角形
11.![]() 的内角
的内角![]() 所对边的长分别为
所对边的长分别为![]() 设向量
设向量![]() ,
,
![]() ,若
,若![]() ,则角
,则角![]() 的大小为( )
的大小为( )
A.![]() B.
B.![]() C.
C. ![]() D.
D. ![]()
12.已知在△ABC中,sinA(sinB+cosB)-sinC=0,sinB+cos2C=0,求角A.B.C的大小.
第四章复习7 三角函数参考答案
一.最值问题
1. ![]() 2.
2.
![]() 3.
3.
![]() 4.D 5.A 6.D 7.B 8.D 9.B
4.D 5.A 6.D 7.B 8.D 9.B
10. 解:函数y=cos2x-asinx+b=1-sin2x- asinx+b,
设sinx=t, -1≤t≤1, y=-t2-at+b+1=-(t+![]() )2+
)2+![]() +b+1,
+b+1,
(1)
当0<a≤2时, ymax=![]() +b+1=0, ymin=-a+b=-4,
+b+1=0, ymin=-a+b=-4,
解得![]() (舍去)或
(舍去)或![]() ,
,
当t=-1即x=![]() 时, ymax
=0, 当t=1即x=
时, ymax
=0, 当t=1即x=![]() 时, ymin
=-4.
时, ymin
=-4.
(2) 当a>2时, ymax=a+b=0, ymin=--a+b=-4,解得a=-2, b=2与a>2矛盾, 舍去.
∴ a=2, b=-2
11. 解:![]() ,
,![]()
二.三角形中的三角函数
1. ![]() 2.
2.
![]() 3. 充要 4.
钝角三角形 5.
3. 充要 4.
钝角三角形 5.
![]()
6.A 解:A 。 ∵![]() ,∴
,∴![]() 。
。
∴![]() ,
,
![]() =
=![]()
![]()
![]() 。
。
7.D 8.D 9.B
10D解:![]() 的三个内角的余弦值均大于0,则
的三个内角的余弦值均大于0,则![]() 是锐角三角形,若
是锐角三角形,若![]() 是锐角三角形,由
是锐角三角形,由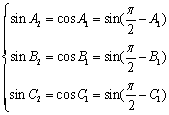 得
得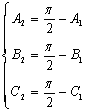 ,那么,
,那么,![]() ,所以
,所以![]() 是钝角三角形
是钝角三角形
11.B 【解析】![]() ,
,
利用余弦定理可得![]() ,即
,即![]() ,
,
12. 解法一 由![]() 得
得![]()
所以![]() 即
即![]()
因为![]() 所以
所以![]() ,从而
,从而![]()
由![]() 知
知![]() 从而
从而![]() .
.
由![]()
即![]()
由此得![]() 所以
所以![]()
![]()