高二年级数学第一学期期终试卷
(试点)
(完卷时间:90分钟 满分:100分) 2007.1
| 题号 | 一 | 二 | 三 | 总分 | ||||
| 1~10 | 11~14 | 15 | 16 | 17 | 18 | 19 | ||
| 得分 | ||||||||
一、填空题(共40分,每小题4分)
1.化简![]() .
.
2.若直线![]() 与直线
与直线![]() 垂直,则直线
垂直,则直线![]() 的方向向量为
.
的方向向量为
.
3.设向量![]() ,
,![]() ,
,![]() ,若向量
,若向量![]() ,
,![]() ,
,![]() ,
,![]() 首尾相接能构成四边形,则向量
首尾相接能构成四边形,则向量![]() .
.
4.边长为1的正方形![]() 中,设
中,设![]() ,
,![]() ,
,![]() ,则
,则![]() .
.
5.一根铁棒在![]() 时长
时长![]() 米,在
米,在![]() 时长
时长![]() 米.若铁棒长度
米.若铁棒长度![]() 和温度
和温度![]() 的关系可以用直线方程来表示,则这根铁棒在
的关系可以用直线方程来表示,则这根铁棒在![]() 时的长度为
米.
时的长度为
米.
6.抛物线![]() 的焦点坐标为
.
的焦点坐标为
.
7.若点![]() 与原点在直线
与原点在直线![]() :
:![]() 的同侧,则实数
的同侧,则实数![]() 的取值范围为
.
的取值范围为
.
8.过椭圆![]() 的中心的直线与椭圆交于
的中心的直线与椭圆交于![]() 、
、![]() 两点,
两点,![]() 是椭圆的右焦点,则
是椭圆的右焦点,则![]() 的面积的最大值为
.
的面积的最大值为
.
9.若双曲线![]() 的两条渐近线的方程为
的两条渐近线的方程为![]() ,则该双曲线方程可以为
.(只需写出一个满足题设的双曲线方程)
,则该双曲线方程可以为
.(只需写出一个满足题设的双曲线方程)
10.下列四个命题;
①直线![]() (
(![]() )的倾斜角的取值范围为
)的倾斜角的取值范围为![]() ;
;
②直线![]() :
:![]() (
(![]() )与直线
)与直线![]() :
:![]() (
(![]() ),则
),则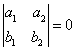 是直线
是直线![]() 、
、![]() 平行的必要不充分条件;
平行的必要不充分条件;
③圆![]() :
:![]() 及点
及点![]() ,若过点
,若过点![]() 作圆
作圆![]() 的两条切线分别交圆
的两条切线分别交圆![]() 于
于![]() 、
、![]() 两点,则过
两点,则过![]() 的直线方程为
的直线方程为![]() ;
;
④方程![]() 不可能表示圆;
不可能表示圆;
其中正确命题的序号为 .
二、选择题(共16分,每小题4分)
11.若点![]() 的坐标为
的坐标为![]() ,曲线
,曲线![]() 的方程为
的方程为![]() ,则
,则![]() 是点
是点![]() 在曲线
在曲线![]() 上的
( )
上的
( )
(A)充分非必要条件 (B)必要非充分条件
(C)充要条件 (D)既非充分又非必要条件
12.若![]() ,
,![]() 都是非零向量,且
都是非零向量,且![]() 与
与![]() 垂直,则下列行列式的值为零的是
( )
垂直,则下列行列式的值为零的是
( )
(A)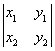 (B)
(B)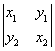 (C)
(C)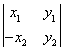 (D)
(D)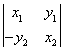
13.若直线![]() 是圆
是圆![]() 的一个切线方程,则直线
的一个切线方程,则直线![]() 的方程可以是 ( )
的方程可以是 ( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
14.设![]() 、
、![]() 是双曲线
是双曲线![]() 的两个焦点,点
的两个焦点,点![]() 在双曲线上,且
在双曲线上,且![]() ,则
,则![]() 的值等于
( )
的值等于
( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
三、解答题(本大题共44分,第15、16、17题每题8分,第18、19题每
题10分)
15.已知直线![]() :
:![]() (
(![]() ,
,![]() )经过点
)经过点![]() ,求直线
,求直线![]() 的倾斜角
的倾斜角![]() (结果精确到
(结果精确到![]() )
)
16.设![]() 是圆
是圆![]() 上任意一点,过
上任意一点,过![]() 作
作![]() 轴,
轴,![]() 为垂足,求线段
为垂足,求线段![]() 的中点
的中点![]() 的轨迹方程,并画出图形.
的轨迹方程,并画出图形.
17.定义:在直角坐标系中,若不在一直线上的三点![]() 、
、![]() 、
、![]() 的坐标分别为
的坐标分别为![]() 、
、![]() 、
、![]() ,则三角形
,则三角形![]() 的面积可以表示为
的面积可以表示为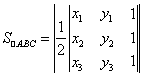 .
.
已知抛物线![]() ,过抛物线焦点
,过抛物线焦点![]() 斜率为
斜率为![]() 的直线
的直线![]() 与抛物线交于
与抛物线交于![]() 、
、![]() 两点.
两点.
(1)求![]() 、
、![]() 两点的坐标;
两点的坐标;
(2)若![]() ,试用行列式计算三角形面积的方法求四边形
,试用行列式计算三角形面积的方法求四边形![]() 的面积
的面积![]() .
.
18.已知平面上三个向量![]() ,
,![]() ,
,![]() 的模均为1,它们相互之间的夹角均为
的模均为1,它们相互之间的夹角均为![]() .
.
(1)求证:![]() ;
;
(2)若![]() (
(![]() ),求
),求![]() 的取值范围.
的取值范围.
19.已知圆锥曲线![]() :
:![]() (
(![]() 且
且![]() ),其两个不同的焦点
),其两个不同的焦点![]() 、
、![]() 同在
同在![]() 轴上.
轴上.
(1)试根据![]() 不同的取值范围来讨论
不同的取值范围来讨论![]() 所表示的圆锥曲线;
所表示的圆锥曲线;
(2)试在曲线![]() 上求满足
上求满足![]() 的点
的点![]() 的个数,并求出相应的
的个数,并求出相应的![]() 的取值范围.
的取值范围.
参考答案:
一、填空题
1.![]() 2.
2.![]() 3.
3.![]() 4.2
5.10.403125 6.
4.2
5.10.403125 6.![]()
7. ![]() 8.12 9.
8.12 9.![]() (答案不唯一) 10.②③④
(答案不唯一) 10.②③④
二、选择题
11~14CDCA
三、解答题
15.解:易知![]() ,
,![]() :
:![]() ,
,![]() ,
,![]()
16. 解:设![]() ,则
,则![]() ,易得
,易得![]()
17.解:![]() ,
,![]() :
:![]()
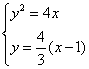
![]()
![]() 、
、![]() ,
,![]()
18.解:![]() ,夹角为
,夹角为![]()
![]() ,所以
,所以![]()
![]()
![]()
由于![]() ,所以
,所以![]()
![]()
19.解:(1)只可能是焦点在![]() 轴上的椭圆或双曲线
轴上的椭圆或双曲线
当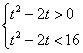 即
即![]() 时,曲线
时,曲线![]() 为焦点在
为焦点在![]() 轴上的椭圆
轴上的椭圆
当![]() 即
即![]() 时,曲线
时,曲线![]() 为焦点在
为焦点在![]() 轴上的双曲线
轴上的双曲线
(2)满足![]() 的
的![]() 在以
在以![]() 为直径的圆周上
为直径的圆周上
当![]() 时,曲线
时,曲线![]() 为焦点在
为焦点在![]() 轴上的双曲线,
轴上的双曲线,![]() 有4个
有4个
当![]() 时,曲线
时,曲线![]() 为焦点在
为焦点在![]() 轴上的椭圆
轴上的椭圆
此时![]() ,
, ![]() ,
,![]()
若![]() ,即
,即![]() 时,
时,![]() 有4个
有4个
若![]() ,即
,即![]() 或
或![]() 时,
时,![]() 有2个
有2个
若![]() ,即
,即![]() 时,
时,![]() 不存在.
不存在.