高考 数学主观题预测题
1 已知函数y=f(x)=
(a,b,c∈R,a>0,b>0)是奇函数，当x>0时，f(x)有最小值2，其中b∈N且f(1)<
(1)试求函数f(x)的解析式；
(2)问函数f(x)图象上是否存在关于点(1，0)对称的两点，若存在，求出点的坐标；若不存在，说明理由
2．在△ABC中，
分别为角A，B，C的对边，且成等比数列．
(I)求∠B的范围；(II)求
的取值范围．
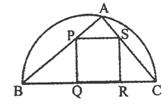
3. 某园林单位准备绿化一块直径为BC的半圆形空地，△ABC外的地方种草，△ABC的内接正方形PQRS为一水池，其余的地方种花。若
，∠ABC=θ，设△ABC的面积为S1，正方形的面积为S2。
（1）用a，θ表示S1和S2；
（2）当a固定，θ变化时，求
取最小值时的角θ。
4、如图，四棱锥P-ABCD中，底面ABCD是矩形，PA⊥底面ABCD，PA=PB=1，AD=
，点F是PB的中点，点E在边BC上移动。
(1)求三棱锥E-PAD的体积；
(2)点E为BC的中点时，试判断EF与平面PAC的位置关系，并说明理由；
(3)证明：无论点E在BC边的何处，都有PE⊥AF；
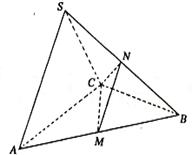
5. 在三棱锥S—ABC中，△ABC是边长为4的正三角形，
平面SAC⊥平面ABC，SA=SC=2
，M、N分别为AB、SB的中点.
（1）证明：AC⊥SB；
（2）求二面角N—CM—B的大小；
（3）求点B到平面CMN的距离.
6. 数列
的前项
和记为
，数列
是首项为2，公比也为2的等比数列．
（Ⅰ）求
；（Ⅱ）若数列
的前项和不小于100，问此数列最少有多少项？
7．设函数
．
（Ⅰ）如果
,点P
曲线
上一个动点,求以P为切点的切线其斜率取最小值时的切线方程；
（Ⅱ）若
时,
恒成立,求
的取值范围．
8． 设数列是首项为6，公差为1的等差数列；
为数列
的前项和，且
（1）求及的通项公式和
；
（2）若
，问是否存在
使
成立？若存在，求出
的值；若不存在，说明理由；
（3）若对任意的正整数，不等式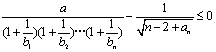
恒成立，求正数
的取值范围。
9. 已知两点M（-2，0），N（2，0），动点P（x,y)在y轴上的射影为H，
是2和
的等比中项.
（1）求动点P的轨迹方程；
（2）若以点M、N为焦点的双曲线C过直线x+y=1上的点Q，求实轴最长的双曲线C的方程.
10. 设抛物线过定点
，且以直线
为准线．
（Ⅰ）求抛物线顶点的轨迹
的方程；
（Ⅱ）若直线
与轨迹交于不同的两点
，且线段
恰被直线
平分，设弦MN的垂直平分线的方程为
，试求
的取值范围．
11．已知函数f(x)定义域为[0，1]，且同时满足
（1）对于任意x∈[0，1]，且同时满足； （2）f(1)＝4；
（3）若x1≥0，x2≥0，x1＋x2≤1，则有 f(x1＋x2)≥f(x1)＋f(x2)－3．
（Ⅰ）试求f(0)的值； （Ⅱ）试求函数f(x)的最大值；
（Ⅲ）设数列{an}的前n项和为Sn，满足a1＝1，Sn＝
(an－3)，n∈N*．
求证：f(a1)＋f(a2)＋…＋f(an)<
log3
．
07届惠来一中文科数学主观题高考预测题参考答案
1 解
(1)∵f(x)是奇函数，
∴f(－x)=－f(x),即
∴c=0,∵a>0,b>0,x>0,∴f(x)=
≥2
，
当且仅当x=
时等号成立，于是2=2,∴a=b2,
由f(1)＜得
＜即
＜,∴2b2－5b+2＜0,解得
＜b＜2，又b∈N,∴b=1,∴a=1,∴f(x)=x+
(2)设存在一点(x0,y0)在y=f(x)的图象上，并且关于(1，0）的对称点(2－x0,－y0)也在y=f(x)图象上，则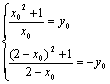
消去y0得x02－2x0－1=0,x0=1±
∴y=f(x)图象上存在两点(1+,2),(1－,－2)关于(1，0)对称
2。解：(I)因为a，b，c成等比数列，所以b2＝ac．
根据余弦定理，得cosB＝＝≥＝．
又因为0＜B＜，所以0＜B≤．所以∠B的范围是(0，]．
(II)y＝2sin2B＋sin(2B＋)＝1－cos2B＋sin2Bcos＋cos2Bsin
＝1＋sin2Bcos－cos2Bsin＝1＋sin(2B－)．
因为0＜B≤，所以－＜2B－≤，所以－＜sin(2B－)≤1，所以＜y≤2．
所以y＝2sin2B＋sin(2B＋)的取值范围是(，2]．
3. （1）
（2分）
设正方形边长为x 则
（4分）
（6分）
（2）当a固定，θ变化时，
（8分）
令
，则
令
函数
在
是减函数
当t=1时，
取最小值，此时
（12分）
4、解：(1) 
(2) 点E为BC的中点时， EF∥平面PAC。
证明如下：∵BE=CE，BF=PF ∴EF∥PC
又EF在平面PAC外，PC在平面PAC内，所以EF∥平面PAC
(3) ∵PA=AB，BF=PF ∴AF⊥PB ∵PA⊥平面ABCD
∴PA⊥BC
又BC⊥AB ∴BC⊥平面PAB 而AF在平面PAB内，
∴AF⊥BC
∵BC、PB是平面PBC内的两条相交直线 ∴AF⊥平面PBC
∵无论点E在BC边的何处，PE都在平面PBC内 ∴PE⊥AF
5. 解：（1）取AC中点D，连结SD、DB.
∵SA=SC，AB=BC， ∴AC⊥SD且AC⊥BD，
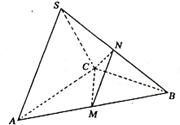∴AC⊥平面SDB，又SB
平面SDB，
∴AC⊥SB ………4分
（2）∵AC⊥平面SDB，AC平面ABC，
∴平面SDB⊥平面ABC.
过N作NE⊥BD于E，NE⊥平面ABC，
过E作EF⊥CM于F，连结NF，
则NF⊥CM.
∴∠NFE为二面角N－CM－B的平面角 ………6分
∵平面SAC⊥平面ABC，SD⊥AC，∴SD⊥平面ABC.
又∵NE⊥平面ABC，∴NE∥SD.
∵SN=NB， ∴NE=SD=
=
=
，
且ED=EB.
在正△ABC中，由平几知识可求得EF=
MB=，
在Rt△NEF中，tan∠NFE=
=2，
∴二面角N—CM—B的大小是arctan2
………10分
（3）在Rt△NEF中，NF=
=
，
∴S△CMN=CM·NF=
， S△CMB=BM·CM=2-------------11分
设点B到平面CMN的距离为h，
∵VB-CMN=VN-CMB，NE⊥平面CMB，
∴
S△CMN·h=S△CMB·NE，∴h=
=
.
即点B到平面CMN的距离为
………14分
6．解：（Ⅰ）由题意
，
∴
．
当
时，
=
，又当
时，
，适合上式，∴
．
（Ⅱ）∵ 
，
∴ 数列
是首项为1，公差为
的等差数列，其前项和为
，故
， 
，得
，
满足它的最小整数是
，即此数列最少有项．
7．解(Ⅰ)设切线斜率为
则
当
时最小值为
．
所以切线方程为
即
(Ⅱ)由>0 <0得．
函数在
为增函数,在
减函数
(1)
,无解； (2)
无解；
(3)
，解得
．综上所述 ．
8． （1）
1分
又当
时，
当
时,
上式对也成立，
∴
， 总之，
（2）由已知
∴当为奇数时，
为偶数,
由，得
,
∴
（舍去）
6分
当为偶数时，为奇数，
由，得
，即
，∴
适合题意。
总之，存在整数，使结论成立 8分
（3）将不等式变形并把
代入得：
设
∴
∴
又∵
∴
，即
∴
随的增大而增大，
， ∴
.
9.解：（1）动点为P（x,y),则H(0,y)，=(-x,0),
=(-2-x,-y),
=(2-x,-y),
∴·=x2-4+y2,且｜2=x2.由题意得2=2·，即x2=2(x2-4+y2),∴
为所求点P的轨迹方程.
(2)若直线x+y=1与双曲线C右支交于点Q时，而N（2，0）关于直线x+y=1的对称点E（1，-1），则QE=QN，
∴双曲线C的实轴长2a=QM-QN=QM-QE≤ME=
(当且仅当Q、E、M共线时取“=”），此时，实轴长2a最大为；
若直线x+y=1与双曲线C左支交于点Q时，同理可求得双曲线C的实轴长2a最大为.
所以，双曲线C的实半轴长a=
.
又∵c=
MN=2,∴b2=c2-a2=
. 故双曲线方程为
.
10 解：（Ⅰ）设抛物线的顶点为
，则其焦点为
．由抛物线的定义可知：
．
所以，
．
所以，抛物线顶点
的轨迹的方程为：
．
（Ⅱ）显然，直线与坐标轴不可能平行，所以，设直线的方程为
，代入椭圆方程得：
由于与轨迹交于不同的两点，所以，
，即
．（＊）
又线段恰被直线平分，所以，
．
所以，
． 代入（＊）可解得：
．
设弦MN的中点
．在
中，令，
可解得：
．
将点
代入，可得：
．
所以，
．
解法二．设弦MN的中点为
，则由点为椭圆上的点，
可知：
．
两式相减得：
又由于
，代入上式得：
．
又点
在弦MN的垂直平分线上，所以，
．所以，
．
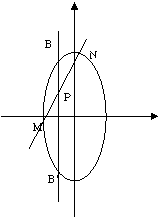
由点在线段BB’上（B’、B为直线与椭圆的交点，如图），所以，
． 也即：
．所以，
.
11解答：（Ⅰ）令x1＝x2＝0，则有f(0)≥2f(0)－3，即f(0)≤3．又对任意x∈[0，1]，总有f(x)≥3，所以f(0)＝3．
（Ⅱ）任取x1，x2∈[0，1]，x1<x2， f(x2)＝f[x1＋(x2－x1)]≥f(x1)＋f(x2－x1)－3．
因为0<x2－x1≤1， ∴f(x2－x1)≥3． ∴f(x2)≥f(x1)＋3－3＝f(x1)．
∴当x∈[0，1]时，f(x)≤f(1)＝4，所以函数f(x) 的最大值为4．
（Ⅲ）当n>1时，an＝Sn―Sn－1＝
(an－3) ―（an－1―3），∴
＝．
∴数列{an}是以a1＝1为首项，公比为的等比数列．
an＝1×()n－1＝
，
f(1)＝f[3n－1·]＝f[＋(3n－1－1)×]≥f()＋f[(3n－1－1)]－3≥……
4≥3n－1f()－3n＋3．
∴f()≤
＝3＋，即f(an)≤3＋．
∴f(a1)＋f(a2)＋…＋f(an)≤(3＋
)＋(3＋
)＋…＋(3＋)
＝3n＋
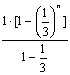＝3n＋－
<3n＋＝3（n＋）．
又log3
＝log333·32n－2＝(2n＋1)＝3(n＋)，
∴原不等式成立．