高考理科数学试题全国Ⅱ卷
（吉林、甘肃、黑龙江、内蒙古、贵州、云南）
一、选择题
（1）已知集合M＝｛xx＜3｝，N＝｛xlog2x＞1｝，则M∩N＝
（A）
（B）｛x0＜x＜3｝
（C）｛x1＜x＜3｝ （D）｛x2＜x＜3｝
（2）函数y＝sin2xcos2x的最小正周期是
（A）2π （B）4π （C） （D）
（3）＝
（A）i
（B）－i （C）
（D）－
(4)过球的一条半径的中点，作垂直于该半径的平面，则所得截面的面积与球的表面积的比为
（A） (B) (C) (D)
(5)已知△ABC的顶点B、C在椭圆＋y2＝1上，顶点A是椭圆的一个焦点，且椭圆的另外一个焦点在BC边上，则△ABC的周长是
（A）2 （B）6 （C）4 （D）12
（6）函数y＝lnx+1(x＞0)的反函数为
（A）y＝ex＋1(x∈R) （B）y＝ex－1(x∈R)
（C）y＝ex＋1(x＞1) (D)y＝ex－1(x＞1)
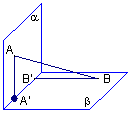（7）如图，平面α⊥平面β，A∈α，B∈β，AB与两平面α、β所成的角分别为和，过A、B分别作两平面交线的垂线，垂足为A′、B′，则AB∶A′B′＝
（A）2∶1 （B）3∶1
（C）3∶2 （D）4∶3
（8）函数y＝f(x)的图像与函数g(x)＝log2x(x＞0)的图像关于原点
对称，则f(x)的表达式为
(A)f(x)＝(x＞0) (B)f(x)＝log2(－x)(x＜0)
(C)f(x)＝－log2x(x＞0) (D)f(x)＝－log2(－x)(x＜0)
（9）已知双曲线的一条渐近线方程为y＝x，则双曲线的离心率为
（A） (B) (C) (D)
(10)若f(sinx)＝3－cos2x，则f(cosx)＝
（A）3－cos2x （B）3－sin2x （C）3＋cos2x （D）3＋sin2x
（11）设Sn是等差数列｛an｝的前n项和，若＝，则＝
（A） （B） （C） （D）
（12）函数f(x)＝的最小值为
（A）190 （B）171 （C）90 （D）45
二、填空题：本大题共4小题，每小题4分，共16分，把答案填在答题卡上
（13）在(x4＋)10的展开式中常数项是 （用数字作答）
（14）已知△ABC的三个内角A、B、C成等差数列，且AB＝1，BC＝4，则边BC上的中线AD的长为
（15）过点（1，）的直线l将圆(x－2)2＋y2＝4分成两段弧，当劣弧所对的圆心角最小时，直线l的斜率k＝
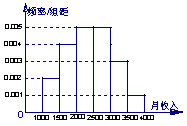
（16）一个社会调查机构就某地居民的月收入调查了10 000人，并根据所得数据画了样本的频率分布直方图（如下图） 为了分析居民的收入与年龄、学历、职业等方面的关系，要从这10 000人中再用分层抽样方法抽出100人作进一步调查，则在［2500，3000）（元）月收入段应抽出
人
三、解答题：本大题共6小题，共74分，解答应写出文字说明，证明过程或演算步骤
（17）（本小题满分12分）
已知向量
＝(sinθ，1)，
＝(1，cosθ)，－＜θ＜
（Ⅰ）若⊥，求θ；
（Ⅱ）求｜＋｜的最大值
（18）（本小题满分12分）
某批产品成箱包装，每箱5件 一用户在购进该批产品前先取出3箱，再从每箱中任意抽取2件产品进行检验 设取出的第一、二、三箱中分别有0件、1件、2件二等品，其余为一等品
（Ⅰ）用ξ表示抽检的6件产品中二等品的件数，求ξ的分布列及ξ的数学期望；
（Ⅱ）若抽检的6件产品中有2件或2件以上二等品，用户就拒绝购买这批产品，求这批产品级用户拒绝的概率
（19）（本小题满分12分）
如图，在直三棱柱ABC－A1B1C1中，AB＝BC，D、E分别为BB1、AC1的中点
（Ⅰ）证明：ED为异面直线BB1与AC1的公垂线；
（Ⅱ）设AA1＝AC＝AB，求二面角A1－AD－C1的大小
（20）（本小题满分12分）
设函数f(x)＝(x＋1)ln(x＋1)，若对所有的x≥0，都有f(x)≥ax成立，求实数a的取值范围
（21）（本小题满分14分）
已知抛物线x2＝4y的焦点为F，A、B是抛物线上的两动点，且＝λ（λ＞0） 过A、B两点分别作抛物线的切线，设其交点为Ｍ
（Ⅰ）证明·为定值；
（Ⅱ）设△ABM的面积为S，写出S＝f(λ)的表达式，并求S的最小值
（22）（本小题满分12分）
设数列｛an｝的前n项和为Sn，且方程x2－anx－an＝0有一根为Sn－1，n＝1，2，3，…
（Ⅰ）求a1，a2；
（Ⅱ）｛an｝的通项公式