高三数学教学案 第九章 直线、平面、简单几何体
第一课时 平面的基本性质
考纲摘录
掌握平面的基本性质;会用斜二侧画法画水平放置的平面图形的直观图,理解用反证
法证明命题的思路,会用反证法证明一些简单的问题.
知识概要
(1)平面的基本性质(三个公理及其三个推论)及其运用(证明三线共点,三点共线,三线共面);
(2)水平放置的平面图形的直观图的画法——斜二测画法的规则;
(3)会用间接证法证明命题(反证法,同一法).
重点难点
(1)运用公理证明三线共点、三点共线;
(2)掌握“图形语言”、“符号语言” .
基础练习
1.下列命题中,正确的是( )
A.首尾相接的四条线段在同一平面内;
B.三条互相平行的线段在同一平面内;
C.两两相交的三条直线在同一平面内;
D.若四个点中的三个点在同一直线上,那么这四个点在同一平面内.
2.下列四个推理过程,错误的是( )
A.![]() ∥
∥![]() ,
,![]() ; B.
; B.![]()
C.![]()
D.A、B、C![]() ,A、B、C
,A、B、C![]() 且A、B、C不共线
且A、B、C不共线![]()
![]() 与
与![]() 重合
重合
3.一个水平放置的平面图形的斜二侧直观图是一个底角为45°,腰和上底长均为1的等腰梯形,则这个平面图形的面积是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.不重合的三条直线,若相交于一点,可以确定____________平面;若相交于两点可确定__________平面;若相交于三点可确定_________平面.
例题讲解
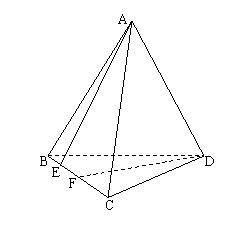
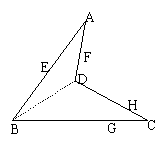 例1.如图,已知在空间四边形ABCD中,E、F分别是AB、AD的中点,G、H分别是BC、CD上的点,且
例1.如图,已知在空间四边形ABCD中,E、F分别是AB、AD的中点,G、H分别是BC、CD上的点,且![]() ,求证:直线EG、FH、AC相交于一点.
,求证:直线EG、FH、AC相交于一点.
例2.如图,已知:![]() ,A、B、C
,A、B、C![]() ,
,![]() ,
,![]() ,
,![]() ,
,
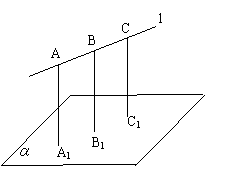 求证:
求证:![]() 共面.
共面.
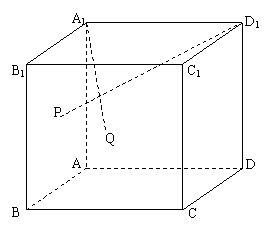
例3.如图,正方体ABCD-A1B1C1D1中,棱长为8㎝,M、N、P分别是
A1B1、AD、BB1的中点;
(1)画出过M、N、P三点的平面与平面ABCD,平面BB1C1C的交线;
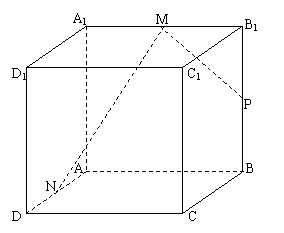 (2)设过M、N、P三点的平面与BC交于Q,求PQ的长.
(2)设过M、N、P三点的平面与BC交于Q,求PQ的长.
例4.如图,在四面体ABCD中作截面PQR,若PQ、CB的延长线交于M,RQ、DB的
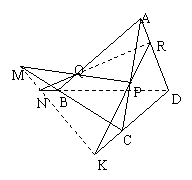 延长线交于N,RP、DC的延长线交于K,求证:M、N、K三点共线.
延长线交于N,RP、DC的延长线交于K,求证:M、N、K三点共线.
课后作业
班级 学号 姓名
1.下列命题中不正确的是( )
①一条直线和两条平行直线都相交,那么这三条直线共面;
②每两条都相交,但不共点的四条直线一定共面;
③两条互相垂直的直线共面;
④两条直线都和第三条相交,那么这两条直线可以确定一个平面
A.①与② B.③与④ C.①与③ D.②与④
2.一条直线和它外面不共线的三点可以确定的平面的个数( )
A.1个或3个 B.1个或4个 C.3个或4个 D.1个、3个或4个
3.平面![]() ∩平面
∩平面![]() ,点A
,点A![]() ,点B
,点B![]() ,且B
,且B![]() ,点C
,点C![]() ,又AC∩
,又AC∩![]() ,过A、B、C三点确定的平面为
,过A、B、C三点确定的平面为![]() ,则
,则![]() ∩
∩![]() 是( )
是( )
A.直线CR B.直线BR C.直线AB D.直线BC
4.若点E、F、G、H依次为空间四边形ABCD四条边AB、BC、CD、DA的中点,EG=3,FH=4,则AC2 +BD2的值为 .
5.已知正方体ABCD-A1B1C1D1中,E、F分别为D1C1,B1C1的中点,AC∩BP=P,
A1C1∩EF=Q
求证:(1)D、B、E、F四点共面;
(2)若A1C交平面DBEF于R点,则P、Q、R 三点共线.
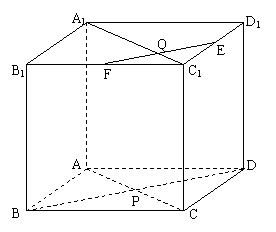
6.已知:直线a,b,c,d是两两相交且不过同一点的四条直线。
求证:直线a,b,c,d共面。
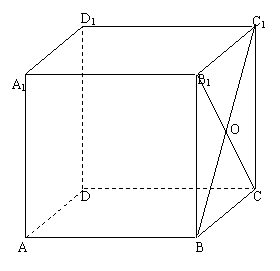
7.(选做题)如图,在棱长为1的正方体ABCD-A1B1C1D1中,M为AB的中点,N为BB1的中点,O为面BCC1B1的中心,
(1)过O作一直线与AN交于P与CM交于Q(只写作法,不必证明)
(2)求PQ的长.
高三数学教学案 第九章 直线、平面、简单几何体
第二课时 直线的位置关系
考纲摘录
能够画出空间两直线的位置关系;能够根据图形想像它们的位置关系.
知识概要
(1)空间两条直线的位置关系,平行公理及等角定理;
(2)异面直线的定义;
(3)判定两直线是异面直线的方法(反证法,异面直线的判定定理).
重点难点
异面直线的定义及判定两直线是异面直线的方法.
基础练习
1.“a、b是异面直线”是指(1)a∩b=![]() ,但a不平行于b;(2)a
,但a不平行于b;(2)a![]() 平面
平面![]() ,b
,b![]() 平面
平面![]() 且a∩b=
且a∩b=![]() ;(3)a
;(3)a![]() 平面
平面![]() ,b
,b![]() 平面
平面![]() 且
且![]() ∩
∩![]() =
=![]() ;(4)a
;(4)a![]() 平面
平面![]() ,b
,b![]() 平面
平面![]() ;(5)不存在任何平面
;(5)不存在任何平面![]() ,能使a
,能使a![]()
![]() 且b
且b![]()
![]() 成立,上述结论中,正确的是( )
成立,上述结论中,正确的是( )
 2.如果一个角的两边和另一个角的两边分别平行,则这两个角关系_____________.
2.如果一个角的两边和另一个角的两边分别平行,则这两个角关系_____________.
3.如图在正方体ABCD-A1B1C1D1中选出两条
棱和两条面对角线,使这四条线段所在的直线
两两都是异面直线,如果我们选定一条面对角
线AB1,那么另外三条线段可以是__________
(只需写出一种情况即可)
4.对于直线m、n和平面![]() ,下列命题中的真命题是( )
,下列命题中的真命题是( )
A.如果m![]()
![]() ,n
,n![]()
![]() ,m,n是异面直线,那么n∥
,m,n是异面直线,那么n∥![]() ;
;
B.如果m![]()
![]() ,n
,n![]()
![]() ,m,n是异面直线,那么n与
,m,n是异面直线,那么n与![]() 相交;
相交;
C.如果m![]()
![]() ,n∥
,n∥![]() ,m,n共面,那么m∥n;
,m,n共面,那么m∥n;
D.如果m∥![]() ,n∥
,n∥![]() ,m,n共面,那么m∥n
,m,n共面,那么m∥n
5.线段AB、CD所在直线是异面直线,M、N分别是AB、CD的中点,则MN_______![]() (AC+BD).
(AC+BD).
例题讲解
例1.如图,已知不共面的三条直线
![]() 相交于点P,
相交于点P,![]()
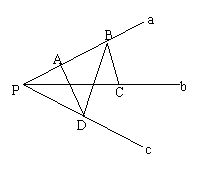 求证:AD与BC是异面直线.
求证:AD与BC是异面直线.
例2.空间四边形ABCD中,E、F分别为BC、CD的中点,G、H分别为AB、AD上的点,且AG:GB≠AH:HD
求证:GH与EF是异面直线.
例3.已知△ABC中,AC的长为定值,D![]() 平面ABC,点M、N分别为△DAB和△DBC的重心
平面ABC,点M、N分别为△DAB和△DBC的重心
求证:无论B、D如何变换位置,线段MN的长为定值.
例4.求证:过直线外一点,有且只有一条直线和这条直线平行.
课后作业
班级 学号 姓名
1.下列四个命题中,正确的是( )
A.两直线无公共点,是这两条直线异面的充分不必要条件
B.两直线无公共点,是这两条直线平行的充分不必要条件
C.两条直线有公共点,是这两条直线共面的必要不充分条件
D.两条直线有公共点,是这两条直线共面的充分不必要条件
2.如果![]() 是异面直线,P是不在
是异面直线,P是不在![]() 上任意一点,下列四个结论:
上任意一点,下列四个结论:
(1)过P一定可作直线![]() 与
与![]() 相交;(2)过P一定可作直线
相交;(2)过P一定可作直线![]() 与
与![]() 都垂直;(3)过P一定可作平面
都垂直;(3)过P一定可作平面![]() 与
与![]() 都平行;(4)过P一定可作直线
都平行;(4)过P一定可作直线![]() 与
与![]() 都平行,其中正确的结论有( )
都平行,其中正确的结论有( )
A.0个 B.1个 C.2个 D.3个
3.过三棱柱两个顶点的直线共15条,其中异面直线有( )
A.18对 B.24对 C.30对 D.36对
4.已知a、b、c是两两异面且互相垂直的三条直线过c作平面![]() 与a垂直,则直线b与平面
与a垂直,则直线b与平面![]() 的位置关系是
.
的位置关系是
.
5.分别和两条直线相交的两条直线的位置关系是 .
6.已知空间四边形ABCD,AB≠AC,AE是△ABC的BC边上的高,DF是△BCD的BC边上的中线
求证:AE和DF是异面直线.
7、在正方体ABCD-A1B1C1D1中,P、Q分别是正方体ABB1A1、BCC1B1的中心,
求证:A1Q与D1P是异面直线.
 |
8、设E、F、G、H分别是空间四边形ABCD各边中点,P、Q分别是两条对角线的中点,
求证:EG、FH、PQ三线共点.
高三数学教学案 第九章 直线、平面、简单几何体
第三课时 直线与平面垂直(一)
考纲摘录
掌握直线与平面垂直的判定定理和性质定理;了解三垂线定理及其逆定理并能运用它
们进行论证和解决问题.
知识概要
直线和平面的位置关系;直线和平面垂直的判定定理和性质定理(线线垂直、线面垂直的相互转化);三垂线定理及其逆定理(“四线一面三垂直”).
重点难点
直线和平面垂直的判定,三垂线定理及其逆定理,并能运用它们进行论证和解决有关问题.
基础练习
1.直线![]() ⊥平面
⊥平面![]() ,①若直线m⊥
,①若直线m⊥![]() ,则m∥
,则m∥![]() ;②若m⊥
;②若m⊥![]() ,则m∥
,则m∥![]() ;③若m∥
;③若m∥![]() ,则m⊥
,则m⊥![]() ;④若m∥
;④若m∥![]() ,则m⊥
,则m⊥![]() ,上述判断正确的是( )
,上述判断正确的是( )
A.①②③ B.②③④ C.①③④ D. ②④
2.一条直线与一个平面的一条斜线在这个平面内的射影垂直,是这条直线与这条斜线垂直的( )
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件
3.已知P是四边形ABCD所在平面外的一点,且P到这个四边形各边的距离相等,那么这个四边形一定是( )
A.圆内接四边形 B.矩形 C.圆外切四边形 D.平行四边形
4.用![]() 表示一个平面,
表示一个平面,![]() 表示一条直线,则
表示一条直线,则![]() 内至少有一条直线与
内至少有一条直线与![]() ( )
( )
A.平行 B.相交 C.异面 D.垂直
例题讲解
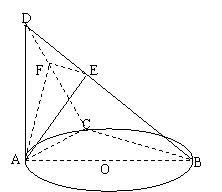
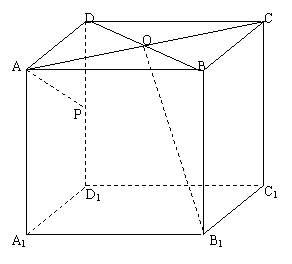
例1.如图,AB为⊙O的直径,点C为⊙O上一点,AD⊥面ABC,AE⊥BD于E,AF⊥CD于F.
求证:BD⊥平面AEF.
 |
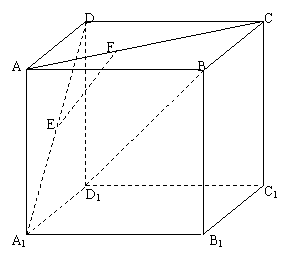
例2.正方体ABCD-A1B1C1D1中,EF是异面直线AC和A1D的公垂线.
求证:EF∥BD1.
例3.在正方体ABCD-A1B1C1D1中,P为DD1的中点,O为底面ABCD的中心,
求证:B1O⊥PA.
课后作业
班级 学号 姓名
1.“垂线![]() 垂直于平面
垂直于平面![]() 内的无数条直线”是
内的无数条直线”是![]() ⊥
⊥![]() 的( )
的( )
A.充分条件 B.必要条件 C.充要条件 D.既不充分也不必要条件
2.在正方体ABCD-A1B1C1D1中与正方体的一条对角线垂直的各面上的对角线的条数是_____________.
3.已知平面![]() 、
、![]() 和直线m,给出条件:①m∥
和直线m,给出条件:①m∥![]() ②m⊥
②m⊥![]() ③m
③m![]()
![]() ④
④![]() ⊥
⊥![]()
⑤![]() ∥
∥![]() ,当满足________时,有m⊥
,当满足________时,有m⊥![]() (填所选条件的序号) .
(填所选条件的序号) .
4.空间四边形ABCD中,AB⊥CD,AD⊥BC,则直线BD与AC的位置关系是 .
5.已知:AB⊥![]() ,CD⊥
,CD⊥![]() ,B、D是垂足,AC⊥
,B、D是垂足,AC⊥![]() ,
,![]() ∩
∩![]() =MN,
=MN,
求证:MN⊥BD.
6、四棱锥S-ABCD中,底面ABCD是正方形,SA⊥平面AC,SC⊥截面AEFG,
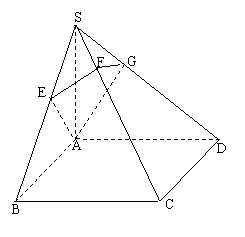 求证:(1)AE⊥SB AG⊥SD;(2)AF⊥GE
求证:(1)AE⊥SB AG⊥SD;(2)AF⊥GE
7、已知PA垂直于矩形ABCD所在平面,M、N分别是AB、PC的中点,
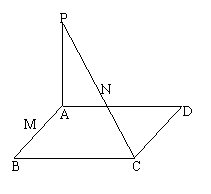 求证:MN⊥AB.
求证:MN⊥AB.
8、(选做题)
过△ABC各边中点D、E、F分别作各边的垂面,这三个垂面能否交于同一条直线,若能交于同一直线,这条交线有什么特点,若不能交于同一条直线,说明理由.
高三数学教学案 第九章 直线、平面、简单几何体
第四课时 直线与平面垂直(二)
目标要求
直线和平面垂直的判定定理和性质定理,三垂线定理的正确运用.
基础练习
1.点P不在三角形ABC所在的平面内,过P作平面![]() ,使三角形ABC的三个顶点到
,使三角形ABC的三个顶点到![]() 的距离相等,这样的平面
的距离相等,这样的平面![]() 共有__________.
共有__________.
2.∠BAC=90°,AB∩![]() =B,AC∩
=B,AC∩![]() =C,则∠BAC在平面
=C,则∠BAC在平面![]() 内的射影∠
内的射影∠![]() (
(![]() )的取值范围是__________.
)的取值范围是__________.
3.正方体ABCD-A1B1C1D1中,点P在侧面BCC1B1及其边界上运动,并且保持AP⊥BD1,则动点P的轨迹是( )
A.线段B1C B.线段BC1
C.BB1中点于CC1中点连成的线段 D.BC中点与B1C1中点连成的线段
4.如图在四面体ABCD中,CD⊥BD,CD⊥AD,△ABC的面内有一点P,过P在平面ABC内画一直线与CD垂直,应如何画?说明理由.
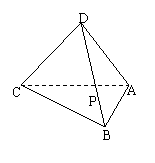 |
例题讲解
例1.如图,已知直三棱柱ABC-A1B1C1中,B1C1= A1C1,A1B⊥AC1
求证:A1B⊥B1C.
 |
例2.如图,已知D是正△ABC所在平面外一点,AD⊥平面ABC,H为A在平面BCD上的射影,
(1)求证:H不可能是△BCD的垂心.
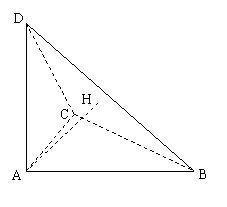 (2)若AB=2,AD=1,求点A到平面BCD的距离.
(2)若AB=2,AD=1,求点A到平面BCD的距离.
例3.正四棱柱ABCD-A1B1C1D1的底面边长为![]() ,侧棱长为3,点E、F分别在BB1,DD1上,且AE交A1B于G,AF交A1D于H,
,侧棱长为3,点E、F分别在BB1,DD1上,且AE交A1B于G,AF交A1D于H,![]() ,
,
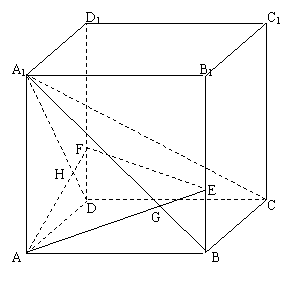 求证:A1C⊥平面AEF.
求证:A1C⊥平面AEF.
课后作业
班级 学号 姓名
1.已知a、b、c是直线,![]() 、
、![]() 是平面,下列条件中,能得出直线a⊥平面
是平面,下列条件中,能得出直线a⊥平面![]() 的是( )
的是( )
A.![]() 其中
其中![]() B.
B. ![]() ∥
∥![]()
C.![]() , a∥
, a∥![]() D.a∥b,
D.a∥b,![]()
2.斜三棱柱ABC-A1B1C1中,∠BAC=90°,BC1⊥AC,则C1在底面ABC的射影H必在( )
 A.直线AB上 B.直线BC上 C.直线CA上 D.△ABC的内部
A.直线AB上 B.直线BC上 C.直线CA上 D.△ABC的内部
3.如图,在正方体ABCD-A1B1C1D1中,
P是侧面BB1C1C内一动点,若P到直线
BC与直线C1D1的距离相等,则动点P的
轨迹所在的曲线是( )
A.直线
B.圆
C.双曲线
D.抛物线
4.在四棱锥P-ABCD中,四条侧棱都相等,底面ABCD为梯形,AB∥CD,AB>CD,为保证顶点P在底面ABCD所在平面上的射影O落在梯形ABCD的外部,则底面ABCD需满足条件 (填上你认为正确的一个充分条件即可).
5.△ABC所在平面![]() 外一点P,过P作PO⊥平面
外一点P,过P作PO⊥平面![]() ,垂足O,连PA、PB、PC.
,垂足O,连PA、PB、PC.
①若PA=PB=PC,则O为△ABC的________心;
②若PA⊥PB,PB⊥PC,PC⊥PA,则O是△ABC的________心;
③若P点到三边AB、BC、CA的距离相等,则O是△ABC的________心;
④若PA=PB=PC,∠C=90°,则O是AB边的__________点;
⑤若PA=PB=PC,AB=AC,则O点在________线上.
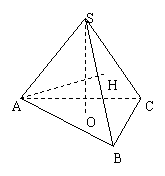 6.已知S-ABC为正三棱锥,AH⊥平面SBC于H,求证H是△SBC的垂心.
6.已知S-ABC为正三棱锥,AH⊥平面SBC于H,求证H是△SBC的垂心.
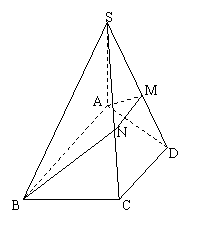
7、如图,在△ABC中,∠BAC=60°,P是△ABC所在平面外一点PA=PB=PC,∠APB=∠APC=90°,
(1)求证:PB⊥平面PAC;
(2)若H是△ABC的垂心,求证:H 是P在平面ABC上的射影.
8、如图在直角梯形ABCD中,∠BAD=∠ADC=90°,CD=DA= a,AB=2a,SA⊥平面ABCD,且SA= a,
(1)求证:△SAD、△SAB、△SDC、△SCB都是直角三角形;
(2)在SD上取点M,SC交平面ABM于N,求证:四边形ABNM为直角三梯形;
 (3)若SM=
(3)若SM=![]() ,写出BM=
,写出BM=![]() 的表达式,并求当
的表达式,并求当![]() 为何值时,BM最小?最小值是多少?
为何值时,BM最小?最小值是多少?
高三数学教学案 第九章 直线、平面、简单几何体
第五课时 线面平行与面面平行
基础知识
掌握直线和平面平行,两个平面平行的判定定理和性质定理.
知识概要
1、直线和平行的判定定理和性质定理,平面与平面平行的判定定理及性质定理;
2、证明直线和平面,平面与平面平行的方法.
重点与难点
线线平行、线面平行、面面平行的不断转化,灵活确定转化的思路和方向.
基础练习
1.直线a⊥平面![]() ,直线b∥
,直线b∥![]() ,则a与b的关系是( )
,则a与b的关系是( )
A.a∥b B.a⊥b C.a、b一定异面 D.a、b一定相交
2.设直线a在平面![]() 内,则
内,则![]() ∥
∥![]() 是直线a∥
是直线a∥![]() 的( )
的( )
A.充分非必要条件B.必要非充分条件 C.充要条件 D.既非充分也非必要条件
3.若直线a与平面![]() 内无数条直线平行,则a与
内无数条直线平行,则a与![]() 的位置关系是( )
的位置关系是( )
A.a∥![]() B.
B.![]() C.a∥
C.a∥![]() 或
或![]() D.
D.![]()
4.以下七个命题:
(1)垂直于同一直线的两个平面平行; (2)平行于同一条直线的两个平面平行;
(3)平行于同一平面的两个平面平行;
(4)一个平面内的两相交直线与另一个平面内的两条相交直线平行,则这两个平面平行;
(5)与同一条直线成等角的两个平面平行;
(6)一个平面上有共线三点到另一个平面的距离相等,则这两个平面平行;
(7)两个平面分别与第三个平面相交所得的两条交线平行,则这两个平面平行.
其中正确命题的序号是___________.
 例题讲解
例题讲解
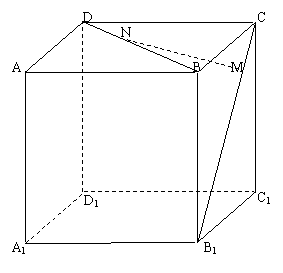
例1. 如图,正方体ABCD-A1B1C1D1中,点N
在BD上,点M在B1C上,且CM=DN,
求证:MN∥平面AA1B1B.
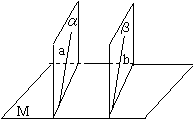
例2.已知a∥b,a,b与平面M斜交,![]() ,且
,且![]() ⊥平面M,
⊥平面M,![]() ⊥平面M,
⊥平面M,
求证:![]() ∥
∥![]() .
.
 |
例3.已知ABCD是平行四边形,点P是平面ABCD外一点,M是PC的中点,在DM上取一点G,过G和AP作平面交平面BDM于GH,
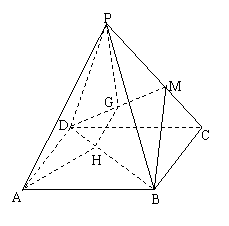 求证:AP∥GH.
求证:AP∥GH.
课后作业
班级 学号 姓名
1.已知直线a、b和平面![]() ,那么a∥b的一个必要不充分的条件是( )
,那么a∥b的一个必要不充分的条件是( )
A.a∥![]() ,b∥
,b∥![]() B.
B.![]() ,
,![]()
C.b![]() 且a∥
且a∥![]() D.a、b与
D.a、b与![]() 成等角
成等角
2.![]() 、
、![]() 表示平面,a、b表示直线,则a∥
表示平面,a、b表示直线,则a∥![]() 的一个充分条件是( )
的一个充分条件是( )
A.![]() 且
且![]() B.
B.![]() ,且
,且![]() ∥b
∥b
C.![]() ∥b且b∥
∥b且b∥![]() D.
D.![]() ∥
∥![]() 且
且![]()
3.一条直线若同时平行于两个相交平面,那么这条直线与这两个平面的交线的位置关系是( )
A.异面 B.相交 C.平行 D.不能确定
4.已知a、b为不垂直的异面直线,![]() 是一个平面,则a、b在
是一个平面,则a、b在![]() 上的射影有可能是:
上的射影有可能是:
①两条平行直线;②两条互相垂直的直线; ③同一条直线; ④一条直线及其外一点
在上面结论中,正确结论的编号是__________.
5.正三棱柱ABC-A1B1C1中,D是A1A上的一点,E是B1C1的中点,且A1E∥平面DBC1,试判断D点在A A1上的位置,并给出证明.
6.如图,ABCD、ABEF均为平行四边形,M、N分别为对角线AC、BF上的点,且有![]() ,
,
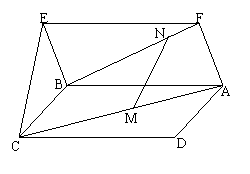 求证:MN∥平面CBE.
求证:MN∥平面CBE.
7、如果一个平面和平面外的一条直线同时垂直于某条直线,那么这条直线和该平面平行.
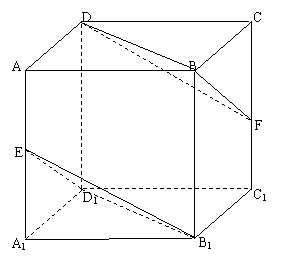 8、已知正方体AC1中,E、F分别是AA1,CC1的中点,求证:平面BDF∥平面B1D1E.
8、已知正方体AC1中,E、F分别是AA1,CC1的中点,求证:平面BDF∥平面B1D1E.
高三数学教学案 第九章 直线、平面、简单几何体
第六课时 线面平行与面面平行
基础知识
线面平行、面面平行的判定和性质的正确运用.
基础练习
1.若夹在两平面间的三条平行线段相等,则这两平面的位置关系__________.
2.若直线a∥平面![]() ,则下列命题中,正确的是( )
,则下列命题中,正确的是( )
A.平面![]() 内有且只有一条直线与a平行 B.平面
内有且只有一条直线与a平行 B.平面![]() 内有无数条直线与a平行
内有无数条直线与a平行
C.平面![]() 内不存在与a垂直的直线 D.平面
内不存在与a垂直的直线 D.平面![]() 内有且只有一条直线与a垂直
内有且只有一条直线与a垂直
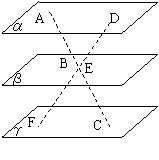 3.直线AC、DF被三个平行平面
3.直线AC、DF被三个平行平面![]() 、
、![]() 、
、![]()
所截,若AC与![]() 成30°,AB=4,BC=12,
成30°,AB=4,BC=12,
DF=10,则平面![]() 、
、![]() 间距离为________,
间距离为________,
DE=________,EF=_______.
4.在正四棱柱ABCD-A1B1C1D1中,E、F、G、H分别为棱CC1,C1D1,D1D,DC的中点,N是BC的中点,点M在四边形EFGH及其内部运动,则M满足条件________时,有MN∥平面B1BDD1.
例题讲解
例1.已知平面![]() ∥平面
∥平面![]() ,AB、CD是异面直线,A
,AB、CD是异面直线,A![]() 、
、![]() ,
,![]() ,
,![]() ,E、F分别为AB、CD的中点,
,E、F分别为AB、CD的中点,
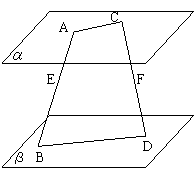 求证:EF∥
求证:EF∥![]() ∥
∥![]() .
.
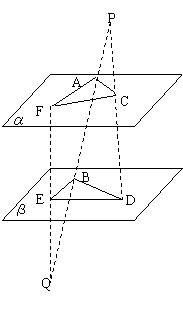
例2.直线PQ分别交两平行平面![]() 、
、![]() 于A、B两点,直线PD分别交平面
于A、B两点,直线PD分别交平面![]() 、
、![]() 于C、D两点,直线QF分别交平面
于C、D两点,直线QF分别交平面![]() 、
、![]() 于F、E两点,若PA=9,AB=12,QB=6,S△ACF=72,求S△BDE.
于F、E两点,若PA=9,AB=12,QB=6,S△ACF=72,求S△BDE.
 |
例4、三个平面两两相交有三条交线,这三条交线或交于一点或互相平行.
课后作业
班级 学号 姓名
1.已知直线m、n及平面![]() ,其中m∥n,那么在平面
,其中m∥n,那么在平面![]() 内到两条直线m、n距离相等的点的集合是( )
内到两条直线m、n距离相等的点的集合是( )
A.一条直线 B.一个平面 C.空集 D.以上都有可能
2.有下列四个命题:
①分别在两个平行平面内的两条直线都平行;
②若两个平面平行,则其中一个平面内的直线必平行于另一个平面;
③如果一个平面内的两条直线平行于另一个平面,则这两个平面平行;
④如果一个平面内的任何一条直线都平行于另一个平面,则这两个平面平行.
其中正确命题的序号为__________.
3.一条直线和一个平面平行,过此直线和这个平面平行的平面有_______个.
4.![]() 、
、![]() 是两个不重合的平面,在下列条件中,可判定
是两个不重合的平面,在下列条件中,可判定![]() ∥
∥![]() 的是( )
的是( )
A.![]() 、
、![]() 都垂直于平面
都垂直于平面![]()
B.![]() 内不共线的三点到平面
内不共线的三点到平面![]() 的距离相等
的距离相等
C.![]() 、m是平面
、m是平面![]() 内的直线,且
内的直线,且![]() ∥
∥![]() ,m∥
,m∥![]()
D.![]() 、m是两条异面直线,且均与平面
、m是两条异面直线,且均与平面![]() 、
、![]() 平行
平行
5.如图,正三棱柱ABC-A1B1C1的底面边长为2,侧棱长为![]() ,D为B1C1的中点
,D为B1C1的中点
(1)求异面直线AC1与BD夹角;
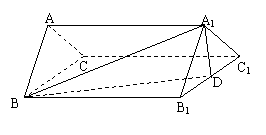 (2)判定AC1与平面A1BD的位置关系并证明.
(2)判定AC1与平面A1BD的位置关系并证明.
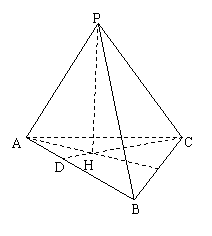
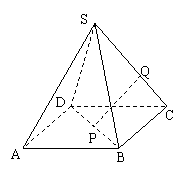 6.如图,正四棱锥S-ABCD的底面边长为a,侧棱长为2a,点P、Q分别在BD和SC上,并且BP:PD=1:2,PQ∥平面SAD,求线段PQ的长.
6.如图,正四棱锥S-ABCD的底面边长为a,侧棱长为2a,点P、Q分别在BD和SC上,并且BP:PD=1:2,PQ∥平面SAD,求线段PQ的长.
7、直三棱柱ABC-A1B1C1中,B1C1= A1C1,AC1⊥A1B,M、N分别是A1B1,AB的中点,
(1)求证:C1M⊥平面A1ABB1;
(2)求证:A1B⊥AM;
(3)求证:平面AMC1∥平面NB1C.
 |
8、已知E、F分别是正方体ABCD-A1B1C1D1的棱AA1、CC1上的点,且AE=C1F,求证:四边形EBFD1是平行四边形.