高三数学教学案 第九章 立体几何
第十八课时 正多面体与球
考纲摘录
了解正多面体的概念，了解欧拉公式，了解球的性质，掌握球的表面积和体积公式；
知识概要
1、多面体、凸多面体、正多面体、简单的多面体定义；
2、球的定义，球的表面积公式、体积公式；
3、球的截面性质，球面距离，经度纬度．
疑点难点
简单多面体中棱数的三种计算方法；球的内接几何体和外切几何体的相关运算．
基础练习
1、下列几何体是正多面体的是（ ）．
A．长方体 B．正四棱柱 C．正三棱锥 D．棱长都相等的三棱锥
2、下列命题为假命题的是（ ）．
A．多面体的面数最少是4 B．正多面体只有五种
C．凸多面体都是简单多面体 D．一几何体的表面经过连续变形为球面的就叫简单多面体
3、过球面上两点可能作球的大圆个数是__________个．
4、在北纬45度圈上有A、B两点，R为地球半径，沿该纬线圈上A、B两点的劣弧长为
，则A、B两点的球面距离为 ____．
5、一个简单多面体的各面都是三角形，且有6个顶点，则这个简单多面体的面数是____个．
6表面积为S的多面体的每一个面都外切于表面积为36π的一个球，则这个多面体的体积为________________．
例题讲解
例1、（1）已知凸多体每个面都是五边形，每个顶点都有三条棱，试求该多面体的棱数、顶点数和棱数．
（2）一个多面体共有10个顶点、每个顶点处都有四条棱，面的形状只有三角形和四边形，求该多面体中三角形和四边形的个数．
例2、在球面上有四点P、A、B、C，若PA、PB、PC两两垂直，且PA=PB=PC=a，
求这个球的表面积、体积以及球心O到截面ABC的距离．
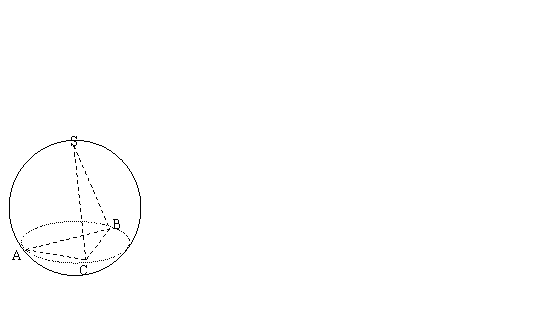
例3、求半径为Ｒ的球Ｏ的内接正三棱锥Ｓ－ABC体积的最大值．
课后作业
班级_______学号__________姓名_________
1、一个凸多面体的各面都是三角形，则它的顶点数V和面数F的关系式是____________．
2、一个多面体的棱数是30，面数是12，则它的各面多边形的内角之和为____________．
3、球A的体积是球B体积的27倍,则球A的表面积是球B表面积的___________倍．
4、正方体的全面积是6a2,它的顶点都在球面上，这个球的表面积是______,体积是_______．
5、正四面体的四个顶点都在表面积为36π的一个球面上，则这个四面体的高等于________．
6、在北纬45度的圈上有甲乙丙三地，甲乙、乙丙之间的经度差都是90度，则甲丙两地的球面距离是甲乙两地球面距离的_________倍．
7、．球面上三点A、B、C组成这个球的一个截面的内接三角形，AB=18，BC=24，AC=30，且球心到该截面的距离为球半径的一半．
（1）求球的体积；
(2)求A、C两点的球面距离．
8、半径为1的球面上有A、B、C三点，其中A和B的球面距离、A和C的球面距离都是
，B和C的球面距离是
，求球心O到平面ABC的距离．
9、正三棱锥的高为1，底面边长为
，此三棱锥内有一个球和四个面都相切．
（１）求棱锥的全面积；
（２）求球的体积．
高三数学教学案 第九章 立体几何
第十九课时 立体几何综合运用（一）
考纲要求
能正确地分析几何体中基本元素及其相互关系，能对图形进行分解、组合与变换；会运用图形和图表等手段形象地揭示问题的本质，进一点提高空间想象能力和逻辑思维能力．
例题讲解
例1.1如图，已知在矩形ABCD中,AB=1,BC=a(a>0),PA垂直平面AC,且PA=1,
(1)问BC边上是否存在点Q,使得PQ⊥QD,并说明理由;
(2)若BC边上有且只有一个点Q,使得PQ⊥QD,求这时二面角Q-PD-A的大小
1.2在四棱锥P-ABCD中,侧棱PA⊥底面ABCD,底面ABCD是矩形,问底面的边BC上是否存在点E,
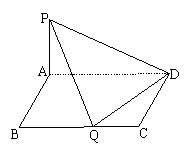(1)使得∠PED=900;
(2)使∠PED为锐角．证明你的结论．
例2、已知菱形ABCD的面积为
，且
BCD=60°，现将其沿对角线BD折成直二面角A－BD－C，（如图所示）
（1）求直线AD与直线BC所成角的余弦值；
（2）求直线BC与平面ACD所成角的大小；
（3）求二面角B-AC-D的大小．
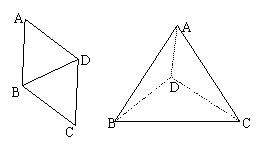
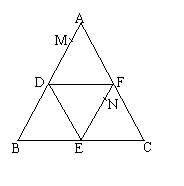例3、如图，正三角形ABC的边长为2，D、E、F分别为各边中点，将△ABC沿DE、EF、DF折叠，使得ABC三点重合，构成三棱锥A－DEF，设点M、N分别在AD、EF上，
（
为变量），若异面直线MN与AE所成的角为
，异面直线MN与DF所成的角为
，求证：
的定值．
课后作业
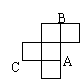班级_______学号__________姓名_________
1、如图，是一个无盖的正方体盒子展开后的平面图，A、B、C是展开图
上的三点，则在正方体盒子中，∠ABC的值为_____________．
2、如图，将边长为
的正方形剪去图中阴影部分，沿图中所画
虚线折成一个正三棱锥，则这个正三棱锥侧棱与底面
所成角的余弦值为_____________．
3、棱长为的正四面体内任意一点到各面距离之和为定值，则这个定值等于_________．
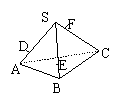4、一个盛满水的三棱锥容器(如图) 其容积为V，发现三条侧棱
上各有一个小洞D、E、F，且知SD:DA=SE:EB=CF:FS=2:1，若
仍用这个容器盛水，则最多可盛原来水的( )．
A 
B 
C 
D 
5、点P在直径为1的球面上，过P作两两垂直的三条弦，若其中一条弦长是另一条的二倍，求这三条弦长之和的最大值．
6、三棱锥各侧面与底面成45°角，底面三角形各角成等差数列，而最大边和最小边的长是方程
两根，求此三棱锥的侧面积和体积．
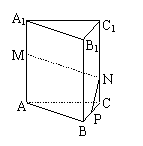
7、在正三棱柱ABC－A1B1C1中，AB=3，AA1=4，M为AA1的中点，P是BC上一点，且由P沿棱柱侧面经过棱CC1到M的最短路线长为
，设这条最短路线与CC1的交点为N．
（1）求该三棱柱的侧面展开图的对角线长；
（2）求PC与NC的长；
（3）求平面NMP与平面ABC所成二面角（锐角）的大小．
高三数学教学案 第九章 立体几何
第二十课时 立体几何综合运用（二）
例题讲解
例1、如图，四棱锥S－ABCD中，AB∥CD，CD⊥面SAD，且
CD=SA=AD=SD=AB=1
（1）当H为SD中点时，求证AH∥平面SBC，平面SBC⊥平面SCD；
（2）求点D到平面SBC的距离；
（3）求面SBC和面SAD所成的二面角的大小．
例2、如图，长方体ABCD－A1B1C1D1中，AB=BC=4，AA1=8，E、F分别为AD和CC1的中点，O1为下底面正方形的中心．
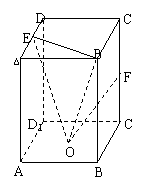求：（1）二面角C－EB－O1的正切值；
（2）异面直线EB与O1F所成角的余弦值；
（3）三棱锥O1－BEF的体积．
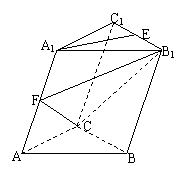例3、如图，在斜三棱柱ABC－A1B1C1中，∠A1AB=∠A1AC，AB=AC，A1A=A1B=，侧面B1BCC1与底面ABC所成的二面角为120°，E、F分别棱B1C1、A1A的中点．
（1）求A1A与底面ABC所成的角；
（2）证明A1E∥平面B1FC；
（3）求经过A1、A、B、C四点的球的体积．
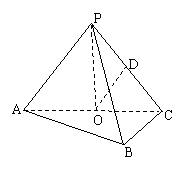
例4、如图，在三棱锥P－ABC中，AB⊥BC，AB=BC=
·PA，点O、D分别是AC、PC的中点，OP⊥底面ABC．
（1）求证：OD∥平面PAB；
（2）当
时，求直线PA与平面PBC所成角的大小；
（3）当为何值时，O在平面PBC内的射影恰好为△PBC的重心？
课后作业
班级_______学号__________姓名_________
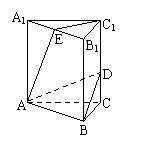1、在正三棱柱ABC－A1B1C1中，BC=
，D、E分别为棱CC1，A1B1的中点，E在平面ABD内的射影G是△ABD的重心
（1）求该棱柱的高；
（2）求直线EA与直线BC所成的角．
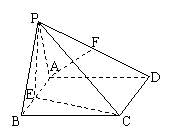
2、如图，四棱锥P－ABCD的底面是矩形，PA⊥底面ABCD于A，E、F分别是AB、PD之中点．
（1）求证：AF∥平面PCE；
（2）若二面角P－CD－B为45°，求证：平面PCE⊥平面PCD；
（3）在（2）的条件下，若AD=2，CD=
，求F点到平面PCE距离．
 |
3、在棱长为的正方体ABCD－A1B1C1D1中，E、F分别是棱AB与BC的中点．
（1）求二面角B－FB1－E的大小； （2）求点D到平面B1EF的距离；
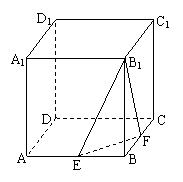（3）在棱DD1上能否找到一点M，使BM⊥平面EFB1，若能，试确定点M位置，若不能，请说明理由．
4、梯形A1A2A3D中有一内接三角形BCD，A1D∥A2A3，A1 A2⊥A2A3，现沿BC，CD，DB将图形翻折起来，使A1A2A3重合为一点A．
（1）求证：AB⊥CD；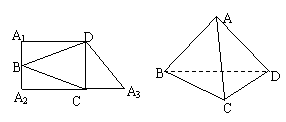
（2）若A1A2=16，A1D=20，求二面角A－CD－B的大小；
（3）求点A到平面BCD的距离．