高三数学教学案 第六章 不等式
班级_______学号__________姓名_________
第一课时 不等式的性质
考纲摘录
1、掌握实数的运算性质及大小顺序之间的关系；
2、理解不等式的性质定理及其推论的证明；
3、能正确使用不等式的性质，进行两个代数式大小的比较，以及判定某些不等式是否成立。
知识概要
知识点：1、实数的运算性质
2、不等式的性质
基本方法：比较两个代数值（或式）的大小：作差比较法与作商比较法．
重点难点
重点：不等式的性质和比较法的应用．
难点：不等式性质及推论的证明．
基础练习
1、设a、b、c∈R，判断下列各命题的真假
1）若a＞b，则ac2＞bc2 2）若ac2＞bc2，则a＞b
3）若a＜b＜0，则a2＞ab＞b2 4）若a＜b＜0，则
＜
5）若a＜b＜0，则a ＞ b 6）若c＞a＞b＞0，则
＞
7）若a＜b＜0，则
＞
8）若a＞b，＞则a＞0，b＜0
2、若
＜a＜b＜0，则有 （ ）
A．＜＜b2＜a2
B．＜＜a2＜b2
C．＜＜b2＜a2 D．＜＜a2＜b2
3、（1）若3≤m＜6，
m＜n＜
（2）若角
、
满足
＜＜＜
，则2
取值范围是_____________．
4、若
,
且
＜1，则
与
的大小关系是____________．
例题讲解
例1、已知三个不等式：ab＞0，bc
＞0，
＞0（其中a、b、c、d均为实数）用其中两个不等式作为条件，余下的一个不等式作为结论组成一个命题，确定可组成的正确命题．
例2、(1)若＜
＜0，试比较
与
的大小
(2)设a＞0，b＞0且a≠b，试比较
·
与
·
的大小。
例3、在等比数列{an}和等差数列{bn}中，a1=b1＞0，a3=b3＞0，且a1≠a3，试比较a2与b2、、、、a5与b5的大小．
例4、设
，且1≤
≤2，2≤
≤4，求
的取值范围。
课后作业
班级_______学号__________姓名_________
1、已知＜＜0，则下列不等式中：①a+b＜ab ② a ＞ b ③ a＜b ④
＞2，正确的不等式个数是________个．
2、已知a、b是实数，则a＞b＞0是
＞
的______________条件．
3、已知a、b∈R，则a+b＜1+ab是+＜1的______________条件．
4、命题“a＞b
＜”成立的充要条件是______________．
5、已知a、b∈(0，+∞)，设A=
+
，B=
，则A、B的大小关系是______________．
6、若a＞1，M=
，N=
，则M与N大小关系是______________．
7、已知a＞2，b＞2，比较a+b与ab的大小．
8、比较
与
的大小．
9、已知0＜＜1，0＜a＜1，试比较
与
的大小。
10、（选做题）设
，根据函数单调性定义，证明函数
在
(1，]上是增函数．
高三数学教学案 第六章 不等式
班级_______学号__________姓名_________
第二课时 算术平均数与几何平均数（一）
考纲摘录
掌握两个（不要求扩展到三个）正数的算术平均数不小于它们的几何平均数这个定理并会用定理证明简单的不等式．
知识概要
1、均值不等式及成立的条件；
2、均值不等式的变式；
3、理解四个“平均数”的大小关系．
重点难点
均值不等式定理及利用均值不等式证明简单不等式．
基础练习
1、若0＜a＜1，0＜b＜1且a≠b，则下列代数式中最大的是 （ ）
A．+ B．a + b C．2ab D．2
2、已知M = () () (
)，a + b +c=1，其中a、b、c∈R
，则M的取值范围是
（ ）
A．
B．
C．
D．
3、已知实数a、b、c∈(0，1)，且a、b、c互不相等，设
=
，
=
，
=
，则、、的大小关系是______________．
4、已知a、b、c∈R，且a+b+c=1，求证
≥6
例题讲解
例1、设a、b∈R，a+b=1，试给出含有a、b两个元素的不等式，并加以证明．
2、已知a、b、c∈R，求证：
(1) 
≥
≥
（2）
≥
例3、设数列{an}是等差数列，并且a1＞1，公差
＞0，求证：
是递减数列．
课后作业
班级_______学号__________姓名_________
1、已知1＜＜，那么
______1．（填“＜”或“＞”）
2、已知a＞b＞0，全集I=R，M={
＜＜
}，N={＜＜
}，
则M∩
= _____________．
3、数列{an}通项公式an=
，则数列{an}中最大项是第_________项．
4、设a、b∈R，a+b=3，则
的最小值是____________．
5、已知a、b∈R，且a+b=2，a≠b，则1，ab，
由小到大的顺序是________________．
6、下列不等式
①
≥2 ②≥2
③若0＜a＜1＜b，则
≤
④若0＜a＜1＜b，则
≤
其中正确的是______________．
7、若0＜a＜b，且a+b =1，试确定
，a，b，
的大小．
8、已知a、b、c∈R，且a+b+c=1，求证：
①
≥
②
≤
9、已知方程
有一根
＞0，求证：方程
必有一根
，使+≥2．
10、（选做题）已知a、b是正数，求证：
①若
＞
，则对于任何大于1的正数x，恒有
＞b成立；
②若对任何大于1的正数x，恒有＞b成立，则＞．
高三数学教学案 第六章 不等式
班级_______学号__________姓名_________
第三课时 算术平均数与几何平均数（二）
考纲摘录
掌握用两个正数的算术平均数不小于它的几何平均数的定理求函数的最值和解决不等式应用题.
知识概要
1、如果a、b∈R，
= P(定值)，当
时，
有最小值2
（简记为：积定和有最小值）
2、如果a、b∈R，=S(定值)，当时，有最大值
．（简记为：和定积有最大值．
重点难点
重点：运用两个正数的算术平均数不小于它们的几何平均数的定理求函数的最值，特别注意条件：“一正、二定、三等”．
难点：运用均值定理解决应用题时数学模型的建立。
基础练习
1、已知
，则
的最小值是______________．
2、已知函数
①若＞0时，当= _________时，函数有最_________值______________；
②若∈（0，
]时，当= _________时，函数有最_________值______________；
③若∈[4，+∞）时，当= _________时，函数有最_________值______________；
3、已知≥
，则
有
（
）
A．最大值
B．最小值 C．最大值1 D．最小值1
4、某工厂要建造一个长方体形状的无盖水池，水池容积是
例题讲解
例1、①若正数、满足
，求
的最小值
②若、∈R，且
，求的最小值．
例2、试确定实数a的取值范围，使对一切实数，不等式
≥0恒成立．
例3、某生产饮料的企业准备投入适当的广告费,对产品进行促销,在一年内,预计年销量Q(万件)与广告费x(万元)之间的函数关系为Q=
(x≥0);已知生产此产品的固定投入为3万元,每生产1万件产品另需再投入32万元,若每件售价为“年平均每件成本的150%”与“年平均每件所占广告费的50%”之和,当年产销量相等.(1)试将年利润y万元表示为年广告费x万元的函数,并判断当年广告费投入100万元时,企业是亏损还是盈利?(2)当年广告费投入为多少万元时,企业年利润最大?
课后作业
班级_______学号__________姓名_________
1、函数
(∈R且≠0)的值域是____________．
2、已知
(
)，
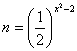（＜0）则与的大小关系是___________．
3、已知
（
，
），则的最小值是____________．
4、已知、是正数且
，则的最小值是___________．
5、若正数、满足
，则的取值范围是___________．
6、周长为定值L的直角三角形的面积最大值是___________．
7、已知、为正数，且
=1，求
的最大值以及达到最大值时的、值．
8、某单位用木料制作如图所示的框架，框架的下部是边长分别是、(单位：m)的矩形，上部是等腰直角三角形，要求框架围成的总面积是、分别为多少时用料最省？
9、求函数
的值域。
10、（选做题）（1）已知a＞b＞0，求
的最小值。
（2）求函数
的最小值。
高三数学教学案 第六章 不等式
班级_______学号__________姓名_________
第四课时 不等式的证明（一）
考纲摘录
掌握用比较法、综合法证明简单的不等式．
知识概要
1、比较法：①作差法 ②作商法
2、综合法：利用已证明过的不等式或不等式性质，从已知条件出发逐步推出所要证明的不等式成立，也就是“由因导果”．
重点难点
重点：运用比较法、综合法证明简单的不等式．
难点：比较法证明中作差（商）后代数式变形技巧．
综合法证明不等式时不等式性质、重要不等式的联想运用．
基础训练
1、设
由小到大的顺序是______________．
2、设
中最大的一个是____________．
3、设实数
的算术平均数是
，任意实数
，记
，则
的大小关系是_________．
4、已知数列
是递增数列，对任意自然数n，
，
恒成立，则实数
的取值范围是____________．
例题选讲
例1、（1）已知
是正数，且
，求证：
．
（2）已知a、是正数，，，且
，求证：
≥
·
+
·
．
例2、已知、b、c是正数，且、b、c成等比数列，求证：
．
例3、已知
，求证：
≥
+．
例4、设，+b =1，
求证：①
≥8 ②
≥
课后练习
班级_______学号__________姓名_________
1、设
都是正数，
·
，则
的大小关系是__________．
2、若
，则
、
的大小关系是__________．
3、设，是常数，则当
的最小值是__________．
4、若，且2
=1，则
的最大值为__________．
5、设
≥________________．
6、已知
，求证：
7、已知
，求证：
＞
8、（1）
，求证：≥
（2）已知
，求证：
≥
9、设
，、是满足
的实数，其中
,
求证：（1）
；（2）2
．
10、（选做题）（1）设、、
均是正数，求证：
≥
（2）设
,
，
求证：
≥
高三数学教学案 第六章 不等式
班级_______学号__________姓名_________
第五课时 不等式的证明（二）
考纲摘录
掌握用分析法证明简单的不等式；了解用反证法证明简单的不等式。
知识概要
1、分析法：从求证的结论出发，逐步寻求使不等式成立的充分条件直至所需的条件被确认成立，从而断定待证不等式成立，也就是“执果索因”．
2、反证法：据“正难则反”原则，解决结论是“至少有一个”、“至多有一个”、“都大于”等类型的问题。其证明的一般步骤是：反设结论 → 逻辑推理 → 导出矛盾 → 肯定结论．
重点难点
重点：用分析法证明简单的不等式．
难点：反证法证明简单不等式过程中矛盾的导出．
基础训练
1、
与
的大小关系是______________．
2、设、b、c不全为O，且=0，则
（
）
A．
B．
C．
、
、
均为负数 D．
＜0
3、设正数、b、c满足
且
，则 （ ）
A．
B．
C．
D．
与大小不定
4、若、
，且
，则
是
的___________条件．
例题选讲
例1、已知，且=0，求证：
．
例2、设
，求证：
≤
．
例3、设
，
，求证：
（
，
）．
例4、用反证法证明：
（1）若
、、
，求证：
、
、
不可能都大于1．
（2）已知
求证：
课后练习
班级_______学号__________姓名_________
1、设
，则下列各式中成立的是
（ ）
A．
B．
C． 
大小不定 D．
2、设
，下列不等式中正确的是
（ ）
A．
B．
C．
D．
3、设是三个互异正数、b、c中的最大数，且
，则
（填“＞”或“＜”）．
4、设、b、c
，则三个数
，
，
的值至少有一个不__________2（填“＞”或“＜”）．
5、设＜1，＜1，则
与2的大小关系是____________．
6、已知，
，2
．求证：
．
7、若
，求证：
．
8、已知，，且
，则
中至少有一个小于2．
9、（1）已知＜1，＜1，求证：
．
（2）求实数的取值范围，使不等式
对一切实数、恒成立，其中
＜1，＜1．
10、（选做题）是否存在常数c,使得不等式
+
≤c≤
对任意正数x、y恒成立?试证明你的结论。
高三数学教学案 第六章 不等式
班级_______学号__________姓名_________
第六课时 不等式的证明（三）
考纲摘录
了解用放缩法、换元法、判别式法等方法证明简单的不等式．
知识概要
放缩法：利用不等式的传递性，对不等式进行放大或缩小，主要放缩的方法有：增项、减项、利用分式的性质、利用不等式的性质、利用函数的性质等。
换元法：主要是三角换元法与增量换元法，注意换元后新变量的取值范围．
判别式法：根据已知或构造出的一元二次方程、一元二次不等式、一元二次函数的根、解集、函数的性质等特征确定出其判别式所应满足的不等式，从而推出欲证的不等式的方法．
基础训练
1、设
，则
与
的大小关系是_______．
2、实数、满足
，则的取值范围是
（ ）
A．＜0 B．≥≤0或≥4 D．＜0或≥4
3、设实数、、、满足
，
（
）则
的最大值是__________．
4、设、、
，
且≤
恒成立，则的最大值是_______________．
例题讲解
例1、已知1≤
≤2，求证：≤
≤3．
例2、求证：（1）2(
-1)＜
（2）
例3、已知a、b∈R，a+b=1，求证：
．
例4、设
，
，且．求证：
．
课后练习
班级_______学号__________姓名_________
1、如果=1，则
的最大值是___________．
2、Rt△ABC中，C=90
，则
的取值范围是_________．
3、已知实数、满足等式
，则的取值范围是__________．
4、已知、
且
，则
的最大值是__________．
5、
，则A与1的大小关系是_________．
6、设
，则
的最小值是___________．
7、已知
，实数满足
，求证：
．
8、已知
，求证对于任意两个不等实数
，
有
．
9、设、是两个不等的正数，且
，求证：
．
10、（选做题）设函数=
+2bx+c（c＜b＜1），f（1）=0，且方程f（x）+1=0有实根。（1）证明：-3＜c≤-1且b≥0；（2）若m方程f（x）+1=0的一个实根，判断f（m-4）的正负并加以证明。