高三复习训练题
数学（八）（不等式1）
命题人：新建二中 黄承禄 审题人：八一中学 殷晴霞
一、选择题：本大题共12小题，每小题5分，共60分。在每小题给出的四个选项中，只有一项是符合题目要求的。
1．已知集合M=xx2<4，N=xx2-2x-3<0，则集合M
N=( )
A．
B．{xx＞3}
C．{x－1＜x＜2
D．{x2＜x＜3
2．不等式1＜x＋1＜3的解集为( )
A．（0，2）
B．（－2，0）
（2，4）
C．（－4，0）
D．（－4，－2）（0，2）
3．若a＜b＜0，则下列不等式中，不能成立的是（ ）
A．
B．
C．
D．
4．若
，A=
，其中a,b
、G、H的大小关系是（
）
A．A≤G≤H B．A≤H≤G C．H≤G≤A D．G≤H≤A
5．若不等式x—1＜a成立的充分条件是0＜x＜4，则实数a的取值范围是（ ）
A．a≥1 B．a≥3 C．a≤1 D．a≤3
6．不等式
的解集为（
）
A．
B．
C．
D．
7．函数
、B（4，2）是其图象上的上的两个点，则不等式f (x＋2) ＜2的解集是（ ）
A．（
B．（—2，2）
C．
D．（0，4）
8．若a＜0，则不等式
的解集是（ ）
A．
B．
C．
D．
9．f (x)=3ax—2a＋1若存在
那么（ ）
A．－1＜a＜
B．a＜－1 C．a＜－1或a＞
D． a＜
 |
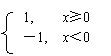10． f (x)= 则不等式x＋(x＋2)f (x＋2)≤5 的解集是（ ）
A．
B．
C．
D．R
11．关于x的不等式ax—b＞0的解集是（
），则关于x的不等式
的解集是（
）
A．
B．（—1，2）
C．（1，2）
D．
12．若x＞y＞z 
，且
恒成立,则n的最大值是（
）
A．2 B．3 C．4 D．5
| 题号 | ||||||||||
| 答案 |
二、填空题：本大题共4小题，每小题4分，共16分。请把答案填在答题卡上。
13．b克糖水中有a克糖（b＞a＞0），若再加入m克糖（m＞0），则糖水更甜了，试根据这个事实写出一个不等式 。
14．如果关于x的不等式a
的解集是
不等式
的解集是
。
15．不等式（x—2）
的解集是
。
16．不等式
的解集是（—3，0）则a=
。
三、解答题：本大题共6小题，共74分。解答应写出文字说明，证明过程或演算步骤。
17．解关于x的不等式
18．设a＞0且a≠1，解关于x的不等式
19．解关于x的不等式
20．已知不等式
（I）求t，m的值；
（2）若函数f(x)=－x2＋ax＋4在区间上递增，求关于x的不等式loga(－mx2＋3x＋2—t)<0的解集。
21．已知函数
。
（1）若对任意的
；
（2）若对任意的x1、
22．已知定义域为[0，1]的函数f(x)同时满足；
（1）对于任意
；
（2）f (x)=1;
（3）若x1≥0, x2≥0, x1＋ x2≤1，则有f (x1＋x2) ≥f (x1)＋f (x2)
( I )试求f (0)的值；（Ⅱ）试求函数
的最大值。
（Ⅲ）（文）试证明：当
当
（IV）（理）试证明：
当
不等式（一）答案
一、选择题
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| C | D | B | A | B | D | B | B | C | A | A | C |
二、填空题
13、
14、
15、
16、
三、解答题
17、解：原不等式等价于
由于
＞
对x
R恒成立 ，∴
＞0即x(x+a)＞0 (6分)
当a
时，
；当a=0时
；当a
时，
18、解：原不等式等价于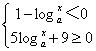
……..(1)或 
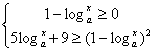………..(2)
由（1）得
>1
由（2）得
由（1）（2）得
当
时，原不等式的解集为
；当
时，原不等式的解集为
19、解：原不等式化为
…………(*)
⑴当 a＞0时，（*）等价于
＜0 
a＞0时，
∴不等式的解为：
＜x＜1
⑵当a=0时，（*）等价于
＜0即x＜1
⑶当a＜0时，（*）等价于＞0 a＜0时，
∴ 不等式的解为 ： x＜1或x＞
综上所述：当a＞0时，不等式的解集为（，1）；当a=0时，不等式的解集为
；
当a＜0时，不等式的解集为∪（，
）
20、解：⑴不等式
＜0的解集为
∴
得
⑵f(x)=
在
上递增，∴
又
，
由
，可知0＜
＜1
由
， 得0＜x＜
由
得x＜
或x＞1
故原不等式的解集为
x0＜x＜或1＜x＜
21、解：⑴令
∴
在
上恒成立，等价于
若
,显然
若
，
且当
时，
；当
时，
∴ 当
， 
=
即
·
解得 a≤5 ∴2＜a≤5
∴ a的范围是
⑵由题意
显然 
=
（当x=0时，取最小值）
a≥0时，g(x)无最大值， 不合题意，∴a＜0.
又
，
∴
，
∴a的范围
.
22、解：（Ⅰ）.令
，依条件（3）可得f (0+0)≥f (0)+f (0),即f (0)≤0
又由条件（1）得f (0) ≥0，则f (0)= 0
（Ⅱ）任取0≤
≤1，可知
，
则
，
即
≥0，故
于是当0≤x≤1时，有f (x) ≤f (1)
=1,因此，当x=1时，f (x)有最大值1
（Ⅲ）证明：当
时，f (x) ≤1<2x
当
时，f (2x) ≥f (x)+f
(x)=2f (x)，∴
（Ⅳ）证明：当时，f (x) ≤1≤2x
当
时，f (2x) ≥f (x)+f
(x)=2 f(x)，∴，
显然，当
时，
·
·
成立
假设当
时，有
成立，其中k=1,2,…
那么当
时，
·
·
·
·
可知对于 ，总有
，其中n∈N*
此时
，故时，有f (x)＜2x (n∈N*)