高三年级数学综合练习（二）
一、选择题（每小题5分，共60分。将正确答案填在答题表内，在每小题给出的四个选项中只有一个是正确的）
1、已知集合
，
，则M∩ P等于（ ）
A．
B．
C．
D．
2、如果
为各项都大于零的等差数列，公差
，则 （ ）
A．
B．
C．
D．
3、当
时，函数
的最小值为
（ ）
A．2 B．
C．4 D．
4、已知函数
在
内是减函数，则 （ ）
A．
B．
C．
D．
5、将直线
沿
轴向左平移1个单位，所得直线与圆
相切．则实数
的值为 （ ）
A．
或7 B．
或8 C．0或10 D．1或11
6、已知直线
与圆
相切，则这三条边长分别为
的三角形 （ ）
A．是锐角三角形 B．是直角三角形 C．是钝角三角形 D．不存在
7、已知定点A、B，且AB=4，动点P满足PA―PB=3，则PA的最小值是 （ ）
A．
B．
C． 
D．5
8、若椭圆
的左、右焦点分别为
，线段
被抛物线
的焦点分成5:3的两段，则此椭圆的离心率为 （ ）
A．
B．
C．
D．
9、在长方体ABCD－A1B1C1D1中，AA1=AB=2，AD=1，点E、F、G分别是DD1、AB、CC1的中点，则异面直线A1E与GF所成的角是 （ ）
A．
B．
C．
D．
10、一个四面体的所有棱长都为
，四个顶点在同一球面上，则此球的表面积为（ ）
A．
B．
C．
D．
11、
的展开式中，
的系数是
（ ）
A．840 B．－840 C．210 D．－210
12、在函数
的图象上，其切线的倾斜角小于的点中，坐标为整数的点的个数是 （ ）
A．3 B．2 C．1 D．0
二、填空题（每小题4分，共24分，将正确答案填在下页的横线上。）
13、设集合
，
，则集合
=____________．
14、若
，则
__________．
15、在函数
中，若
成等比数列，且
，则
有最_______值（填“大”或“小”），且该值为_________．
16、连接抛物线上任意四点组成的四边形可能是___________（填上所有正确选项的序号）．
①菱形 ②有3条边相等的四边形 ③梯形 ④平行四边形 ⑤有一组对角相等的四边形
17、设双曲线
的右焦点为F，右焦点
与两条渐近线交于P、Q两点，如果△PQF是直角三角形，则双曲线的离心率
___________．
18、从6名男生和4名女生中，选出3名代表，要求至少有1名女生，则不同的选法共有___________种（填数字）．
班级________学号________姓名_________
一、选择题（每小题5分，共60分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
二、填空题（每小题4分，共24分）
13、___________________________． 14、___________________________．
15、___________________________． 16、___________________________．
17、___________________________． 18、___________________________．
三、简答题（本大题计5小题，共66分）
19、（本小题满分12分）
已知双曲线中心在原点，且一个焦点为
，直线
与其相交于M、N两点，MN中点的横坐标为
，求此双曲线的方程．
20、（本小题满分12分）
已知向量
，
且
（1）若
，求的解析式；
（2）求函数的最大值和最小值．
21、（本小题满分14分）
设
为实数，函数
．
（1）求的极值；
（2）当在什么范围内取值时，曲线
与轴有且仅有一个交点．
22、（本小题满分14分）
已知如图ABCD－A1B1C1D1是正四棱柱，侧棱长为1，底面边长为2，E是棱BC的中点，
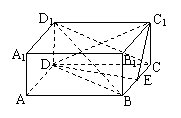（1）求三棱锥D1－DBC的体积；
（2）证明：BD1∥平面C1DE；
（3）求面C1DE与面CDE所成二面角的正切值．
23、（本小题满分14分）
已知数列
的前
项和为
，设集合
，
．
（1）求数列的通项公式；
（2）若以集合A中的元素作为点的坐标，则这些点是否都在同一条直线？并说明理由；
（3）“A∩B至多只有一个元素”是否正确？如果正确，请给予证明；如果不正确，请举例说明．