高三年级数学综合练习(一)
班级__________学号__________姓名__________
一、选择题(每小题5分,共60分。将正确答案填在答题表内,在每小题给出的四个选项中只有一个是正确的)
1、已知集合![]() ,
,![]() ,则集合
,则集合![]() 的子集个数最多有 ( )
的子集个数最多有 ( )
A.1个 B.2个 C.4个 D.8个
2、已知定义在R上的函数![]() 对任意两个不等实数
对任意两个不等实数![]() 、
、![]() ,总有
,总有![]() 成立,则必有 ( )
成立,则必有 ( )
A.函数![]() 是奇函数 B.函数
是奇函数 B.函数![]() 是偶函数
是偶函数
C.![]() 在R上是增函数 D.
在R上是增函数 D.![]() 在R上是减函数
在R上是减函数
3、若![]() ,那么
,那么![]() 的值等于 ( )
的值等于 ( )
A.![]() B.
B.![]() C.
C.![]() D.2
D.2
4、在数列![]() 中,若
中,若![]() ,则下列各不等式中一定成立的是( )
,则下列各不等式中一定成立的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5、已知△ABC的三个顶点A、B、C及平面ABC内一点P满足:![]() ,则点P与△ABC的位置关系为 ( )
,则点P与△ABC的位置关系为 ( )
A.P在△ABC内部 B.P在△ABC外部
C.P在AB边所在直线上 D.P是AC边的一个三等分点
6、设![]() 均为非零实数,不等式
均为非零实数,不等式![]() 和
和![]() 的解集分别是非空集合M、N,那么“
的解集分别是非空集合M、N,那么“![]() ”是“M=N”的 ( )
”是“M=N”的 ( )
A.充分非必要条件 B.必要非充分条件
C.充要条件 D.既非充分又非必要条件
7、过抛物线![]() 上一点A(4,2)作倾斜角互补的两条直线AB、AC交抛物线于B、C两点,则直线BC的斜率为 ( )
上一点A(4,2)作倾斜角互补的两条直线AB、AC交抛物线于B、C两点,则直线BC的斜率为 ( )
A.![]() B.
B.![]() C.
C.![]() D.不能唯一确定
D.不能唯一确定
8、![]() 、
、![]() 分别为椭圆
分别为椭圆![]() 的左、右焦点,AB为其过点
的左、右焦点,AB为其过点![]() 且斜率为1的弦,则
且斜率为1的弦,则
![]() ·
·![]() 的值为( )
的值为( )
A.![]() B.
B.![]() C.
C.![]() D.5
D.5
9、已知定义在R上的函数![]() 对于任意
对于任意![]() ,都有
,都有![]() ,
,
设![]() ,则数列
,则数列![]() 中,值不同的项至多有 ( )
中,值不同的项至多有 ( )
A.12项 B.8项 C.6项 D.4项
10、曲线![]() 和直线
和直线![]() 在
在![]() 轴右侧的交点按横坐标从小到大依次记为
轴右侧的交点按横坐标从小到大依次记为![]() 、
、![]() 、
、![]() ,……,则
,……,则![]() 等于 ( )
等于 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
11、棱长为![]() 的正方体中,连接相邻面中心,以这些线段为棱的八面体中,互相平行的两个面的距离是 (
)
的正方体中,连接相邻面中心,以这些线段为棱的八面体中,互相平行的两个面的距离是 (
)
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
12、边长为![]() 、
、![]() 、
、![]() 的三角形,其面积为0.25,而外接圆半径为1,若
的三角形,其面积为0.25,而外接圆半径为1,若![]() ,
,![]() ,则S与T的大小关系是 (
)
,则S与T的大小关系是 (
)
A、S>T B、S=T C、S<T D、不确定
二、填空题(每小题4分,共24分,将正确答案填在下页的横线上。)
13、当![]() 时,不等式
时,不等式![]() (
(![]() 为常数,
为常数,![]() >0,且
>0,且
![]() ≠1)成立,则此不等式的解集是
.
≠1)成立,则此不等式的解集是
.
14、等差数列![]() 中,
中,![]() ,
,![]() ,则前20项和
,则前20项和![]() .
.
15、购买一件售价为![]() 元的商品,采用分期付款,要在m个月内分m次付款还清,月利率为
元的商品,采用分期付款,要在m个月内分m次付款还清,月利率为![]() ,则每次付款数为
.
,则每次付款数为
.
16、已知![]() 满足
满足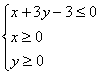 ,则
,则![]() 的取值范围是
.
的取值范围是
.
17、已知向量![]() ,
,![]() ,则向量
,则向量![]() 与
与![]() 夹角为
.
夹角为
.
18、已知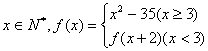 ,其值域为D,给出下列数值:
,其值域为D,给出下列数值:![]() ,
,
![]() ,9,14,27,65,则其中属于集合D的元素是 .(写出所有可能的数值)
,9,14,27,65,则其中属于集合D的元素是 .(写出所有可能的数值)
班级__________学号__________姓名__________
一、选择题(每小题5分,共60分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
二、填空题(每小题4分,共24分)
13、_________________. 14、_________________.
15、_________________. 16、_________________.
17、_________________. 18、_________________.
三、解答题(本大题计5小题,共66分)
19、(本小题满分12分)
已知![]() .
.
(1)若![]() 在
在![]() 上的最大值与最小值之和为3,求
上的最大值与最小值之和为3,求![]() 的值;
的值;
(2)在(1)的条件下,![]() 先按
先按![]() 平移再经过伸缩变换后得到
平移再经过伸缩变换后得到![]() ,求
,求![]() .
.
![]()
![]()
20、(本小题满分12分)
已知![]() ,
,![]() ,设
,设![]() 和
和![]() 的导数分别为
的导数分别为![]() 和
和![]() ,解关于
,解关于![]() 的不等式
的不等式![]()
![]() >0.
>0.
21、(本小题满分14分)
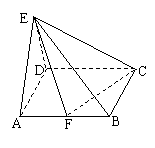 如图,四棱锥E-ABCD中,底面ABCD是矩形且AB=2BC=2,侧面△ADE是正三角形且垂直于底面ABCD,F是AB的中点,AD中点为O,
如图,四棱锥E-ABCD中,底面ABCD是矩形且AB=2BC=2,侧面△ADE是正三角形且垂直于底面ABCD,F是AB的中点,AD中点为O,
求:(1)异面直线AE与CF所成角;
(2)点O到平面EFC的距离;
(3)二面角E-FC-D的大小.
22、(本小题满分14分)
已知函数![]() 在区间[0,1]上单调递增,在区间[1,2]上单调递减.
在区间[0,1]上单调递增,在区间[1,2]上单调递减.
(1)求![]() 的值;
的值;
(2)设![]() ,若方程
,若方程![]() 的解集恰好有3个元素,求
的解集恰好有3个元素,求![]() 的取值范围;
的取值范围;
(3)在(2)的条件下,是否存在实数对(m,n),使![]() 为偶函数?如存在,求出m,n;如不存在,说明理由.
为偶函数?如存在,求出m,n;如不存在,说明理由.
23、(本小题满分14分)
双曲线C的方程为![]() ,过右焦点F(
,过右焦点F(![]() )作双曲线在第一、三象限的渐近线的垂线
)作双曲线在第一、三象限的渐近线的垂线![]() ,垂足为P,且
,垂足为P,且![]() ·
·![]() .
.
(1)求双曲线C的方程;
(2)记双曲线C的左、右顶点分别为A、B,又M为双曲线C上任一动点,点Q满足
![]() ·
·![]() ,
,![]() ·
·![]() ,试求动点Q的轨迹方程.
,试求动点Q的轨迹方程.