高三数学回味练习一
1、有四个式子：(1)
；(2)
；(3)
；(4)
，其中正确式子的个数为 （ ）
（A）1 （B）2 （C）3 （D）4
2、与圆
相切、且在两坐标轴上截距相等的直线有（ ）
（A） 6条 （B） 2条 （C） 3条 （D） 4条
3、若曲线
与直线
相切，则常数
的值为
.
4、
是
的 （ ）
（A）充分非必要条件 （B）必要非充分条件
（C）充要条件 （D）既非充分又非必要条件
5、已知
，则把向量
按向量
平移后得到的向量是（ ）
（A）（3，0） （B）（3，5） （C）（－4，3） （D）（2，3）
6、设平面内有四个向量
，满足
.设
为
的夹角，则
=
.
7、已知正四棱锥
的高为4，侧棱与底面所成的角为
，则该正四棱锥的侧面积是
.
8、下列函数中，有反函数的是 （ ）
（A）
（B）
（C）
（D）
9、如果数列
的前
项的和
，那么这个数列（ ）
（A）是等差数列而不是等比数列 （B）是等比数列而不是等差数列
（C）既是等差数列又是等比数列 （D）既不是等差数列也不是等比数列
10、若圆
关于直线
对称，则 （ ）
（A）
（B）
（C） 
且
（D）
11、已知椭圆
与双曲线
）具有相同的焦点
，设两曲线的一个交点为
，∠
，则双曲线的离心率为
.
12、设集合
映射
，满足条件“对任意的
是奇数”.这样的映射
的个数为 （ ）
（A）10 （B）11 （C）12 （D）13
13、函数
是偶函数，且
不恒等于零，则函数的奇偶性是
（ ）
（A）奇函数 （B）可能是奇函数也可能是偶函数
（C）偶函数 （D）既不是奇函数也不是偶函数
14、在
的展开式中，第十项是二项式系数最大项，则的值是（ ）
（A）18 （B）17或19 （C）19 （D）17，18或19
15、已知
是椭圆
上的一点，是椭圆的两个焦点，点在线段
上，且
，则分
的比为
（ ）
（A）2 ：5 （B）5 ：3 （C）3 ：4 （D）4 ：3
16、①
既不是奇函数，也不是偶函数；②若
是第一象限的角，则
为减函数；③若A是一个三角形的内角，则
有最大值
，最小值不存在；④函数
的最小正周期是
.
上述4个命题中，真命题的序号是 .
17、下列命题中，（1）若
且
，则
或
；（2）若
，则
或；（3）若不平行的两个非零向量
满足
，则
；（4）若
与
平行，则；（5）若
，则
；
其中真命题的个数是 （ ）
（A）1 （B）2 （C）3 （D）4
18、设
，则
的充分不必要条件是 （ ）
（A）
或
（B）
或
（C）
（D）
19、8人坐成一排，现要调换3人的位置，其余5人位置不动，共有 种换法.
20、已知全集
，集合
则（
等于 （ ）
（A）
（B）
（C）
（D）
21、已知函数
在
内是增函数，则
的取值范围是
.
22、已知全集，集合
或
，集合
且（
，则实数
的取值范围是 （ ）
（A）
（B）
（C）
（D）
23、若
，且是奇函数，
是偶函数，则
从小到大的顺序是
.
24、
展开式中的第
项的系数是 （ ）
（A）
（B）
（C）
（D）
25、已知函数的定义域为
，则函数
的定义域为（ ）
（A）
（B） （C）
（D）
26、已知
是第二象限角，且
，则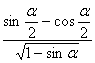
= .
27、已知函数在上是偶函数，在
时，是增函数，那么，当
且且
时，有 （ ）
（A）
（B）
（C）
（D）无法确定
28、直三棱柱
的体积为
分别为
上的点，而且满足
，则四棱锥
的体积是
（ ）
（A）
（B）
（C）
（D）
29、已知
是偶函数，当
时，
，当
时，记的最大值为，最小值为，则
.
30、若函数
在区间
内是增函数，则的取值范围是
.
31、将容量为100的样本数据，按从小到大的顺序分成8个组，如下表：
| 组号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 频数 | 11 | 14 | 12 | 13 | 13 | 12 | 10 |
则第6组的频率为_______.