高三数学教学案 第八章 圆锥曲线
第十一课时 含参系数的曲线方程（一）
考纲摘录
根据曲线方程研究它的几何性质．
难点疑点
用分类讨论的思想讨论含参数的曲线方程所表示的曲线的几何性质，注意分类讨论的“不重不漏”原则及基本的分类讨论方法（二分法）．
基础练习
1、已知：
，曲线
=1，当
时，它表示一个圆；当时它表示双曲线；当时它表示两条平行直线．若该曲线是椭圆，则该椭圆的短轴两端点坐标分别是__________，离心率
．
2、若方程
表示两个焦点都在
轴上的椭圆，则
．
3、方程
所示的曲线是（ ）
A．焦点在轴上的椭圆 B．焦点在
轴上的椭圆
C．焦点在轴上的双曲线 D．焦点在轴上的双曲线
4、方程
表示双曲线时，
；无论
在上述范围内如何变化，方程所表示的这些双曲线有相同的_____________．
例题讲解
例1、设关于、的方程
，（1）当
为何值时，此方程表示圆C；（2）若（1）中的圆C与直线
的两交点M、N满足OM⊥ON（O为原点）求此时的值．
例2、设椭圆
的两个焦点是
，
（
），且椭圆上存在一点P，使得
，求的范围．
例3、直线
与双曲线
的左支交于A、B两点，直线
经过点
和AB的中点，求：直线在轴上的截距
的取值范围．
课后作业
班级_______学号__________姓名_________
1、椭圆
的离心率
，则m=_________．
2、圆
与抛物线
的准线相切，则m=_________．
3、曲线的焦距是_________．
4、曲线C的方程为
，当_________时，曲线C是圆；当_________时，C为椭圆；当_____________时，C为双曲线；当____________时，C为两直线．
5、曲线
的一条准线方程是
，则
=_________．
6抛物线的
顶点为O，焦点是F，若P是抛物线上一点，对于△POF的形状下列说法：①可能为等腰三角形 ②可能为等腰直角三角形 ③可能为正三角形．其中正确的是____________．
7、过抛物线上一定点
，作两条直线交抛物线于
，
（1）求：抛物线上纵坐标为
的点到焦点F的距离；
（2）当PA与PB的斜率存在且倾斜角互补时，求
的值．
8、设椭圆
：
，曲线
：
，且与在第一象限内只有一个公共点P．
（1）试用表示
的坐标；
（2）设A、B是椭圆的两个焦点，当变化时，求△ABP的面积函数
的值域；
（3）记
为
中最小的一个，设
是以椭圆的半焦距为边长的正方形的面积，求：
的表达式．
高三数学教学案 第八章 圆锥曲线
第十二课时 含参系数的曲线方程（二）
考纲摘录
根据曲线方程研究它的几何性质．
难点疑点
对曲线方程中参数范围的讨论，应注意应用函数、不等式等数学思想方法．
基础练习
1、动点P分别与两个定点
，
连线的斜率之积等于，则当
时，动点P在一个圆周上运动；当______________时，P在一个椭圆上运动；当_________时，P在一条双曲线上运动．
2、抛物线
，与直线·
+·
=
·的位置关系是__________．
3、点
在曲线
，则
的范围是__________．
4、实数
变化时，直线
：
恒过直线
：
上的一个定点，则点
满足的曲线方程是_____________．
例题讲解
例1、求证：当
时，方程
表示的曲线具有相同的焦点．
例2、椭圆
的焦点在轴上，A是右顶点，椭圆与射线
的交点是B，以A为焦点，过点B且开口向左的抛物线顶点为
，当椭圆离心率
时，求：的范围．
例3、函数
．①取何值时，的最小值是0？
②求证：不论是什么值，函数图象的顶点在同一直线上．
③平行于的直线中，哪些与抛物线相交？哪些不与抛物线相交？
④求证：任一平行于且与抛物线相交的直线，被抛物线截出的线段都相等．
课后作业
班级_______学号__________姓名_________
1、a、b、c分别是双曲线的实半轴，虚半轴和半焦距，若方程
无实根，则离心率
_________．
2、正三角形的三个顶点在双曲线
的右支上，其中一个顶点是双曲线的右顶点，则m
________．
3、椭圆
与双曲线
共焦点F1，F2，P是两曲线交点，则PF1·PF2的值是_________(
)．
4、抛物线
，横坐标为4的点到焦点的距离为5，则P=___________．
5、椭圆
，点P是
时对应的点，则直线OP的倾斜角为____________．
6、椭圆的两个焦点是
且椭圆上存在点P，使直线．
（1）求：的范围；
（2）设是相应于焦点
的准线，直线
与相交于点
，若
，求：直线的方程．
7、△
的面积是
，且
，
（1）设
，求：
与
的夹角
的范围；
（2）设以O为中心，F为焦点的双曲线过Q，
，当
取最小值时的曲线方程．
8、
，直线：
，：
．
求：到、的距离之和为定值
的点的轨迹．
高三数学教学案 第八章 圆锥曲线
第十三课时 定点、定值、最值问题
考纲摘录
掌握圆锥曲线的简单几何性质．
难点疑点
1、定点问题，常有两类处理办法：一是将曲线方程整理成关于这个参数的方程，运用恒等式的有关知识求得定点的坐标；二是先给定参数的特定参数，求出对应的几条曲线的交点坐标，再代入到曲线方程中逐一验证．
2、定值问题，常通过“算”的办法加以证明，以算代证．
3、最值问题常通过建立目标函数或目标量的不等式进行研究，另外还要注意运用“数形结合”、“几何法”求最值．
基础练习
1、动直线
，不论m取何值，该直线必过定点__________．
2、椭圆
的短轴为B1B2，点M是椭圆上除B1，B2外的任意一点，直线MB1，MB2在轴上的截距分别为
，则
=__________．（用数值做答）
3、双曲线
上任一点P到两条渐近线的距离之积等于__________．（用含的代数式表示）
4、两点A(3，0)，B(0，4)，动点在线段AB上运动，则
的最大值是（ ）
A．
B．3 C．
D．4
例题讲解
例1、设是常数，求：点
与椭圆
上的点所连线段长的最大值．
例2、已知：顶点为原点O，焦点在轴上的抛物线，其内接△ABC的重心是焦点F，若直线BC的方程为：
．
（1）求：抛物线方程；
（2）轴上是否存在定点M，使过M的动直线与抛物线交于P、Q两点，满足∠POQ=90°？证明你的结论．
例3、定椭圆的左焦点为F，过F点的直线交椭圆于A、B两点，P为线段AB的中点，当△PFO的面积最大时，求：直线的方程．
课后作业
班级_______学号__________姓名_________
1、已知：
，则
的最大值是_________，最小值是_________．
2、已知：点A(0，3)，B(4，5)，点P在轴上，则PA+PB的最小值为________．
3、点在椭圆
上运动，则的最大值等于___________．
4、已知：函数
的图象无论m取何值(m≠0)恒过定点，则该定点的坐标是_________________．
5、抛物线
上的点P到直线：
的距离最小，则P的坐标____________．
6、由椭圆的顶点
引弦BP，
求：BP长的最大值．
7、已知：椭圆
的右准线与轴相交于E，过椭圆右焦点F的直线与椭圆交于A、B两点，点C在右准线上，且BC∥轴．
求证：直线AC过线段EF中点．
8、动直线与抛物线
相交于A、B两点，M是AB的中点，若M始终落在曲线
上，求证：直线过定点．
高三数学教学案 第八章 圆锥曲线
第十四课时 解析几何综合应用
考纲摘录
掌握解析几何的一些综合应用．
例题讲解
例1、双曲线C：
，若C的上半支的顶点为A，且与直线
交于点P，以A为焦点，M(0，m)为顶点的开口向下的抛物线通过P，当C的一条渐近线的斜率在区间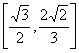
上变化时，求直线PM斜率的最大值．
例2、抛物线
及定点
，M是抛物线上的点，设直线AM、BM与抛物线的另一交点分别为M1，M2．
求证：当点M在抛物线上变动时（只要M1，M2存在且M1，M2是不同的两点），直线M1，M2恒过一定点，并求定点坐标．
例3、椭圆
的焦点在轴上，A是它的右顶点，这个椭圆与射线的交点是B，以A为焦点，过点B且开口向左的抛物线顶点是（m，0），当椭圆离心率时，求：m的范围．
例4、△
的面积是S，且
（1）若
，求：向量与的夹角的范围；
（2）设
，若以O为中心，F为焦点的椭圆，经过点，求：的纵坐标；
（3）在（2）的条件下，当
取得最小值时，求：此椭圆的方程．
课后作业
班级_______学号__________姓名_________
1、双曲线
的两个焦点为
，若P在双曲线上，若，则P到轴的距离是_________．
2、椭圆的两焦点是，点P在椭圆上，且
的最大值为
，则离心率为________．
3、一个酒杯的轴截面是抛物线的一部分，其标准方程是
，在杯中放一小球，要使该球触及杯底，则球的半径
的范围是___________．
4、若抛物线
上存在关于直线
对称的两点，则的范围是（ ）
A． B．（0，2） C．
D．∪
5、A、B为过椭圆中心的弦，
是右焦点，则
的面积的最大值是___________．（用a、b、c表示）
6、顶点为原点O，焦点在轴上的抛物线，其内接△ABC的重心是焦点F，若直线BC的方程是：
．
（1）求：抛物线方程；
（2）轴上是否存在定点M，使过M的动直线与抛物线交于P、Q，且满足
，证明你的结论？
7、椭圆，A、B是椭圆上不同的两个点，线段AB的中垂线与轴相交于点
求证：
．