2005年 专题复习四 数列
[高考要点]
1． 理解数列的有关概念，了解递推公式是给出数列的一种方法，并能根据递推公式写出数列的前几项。
2．
掌握等差数列与等比数列的概念、通项公式、前
项和的公式，并能运用这些知识解决一些问题。
3．
了解数列极限的意义，掌握极限的四则运算法则，会求公比的绝对值小于1的无穷递缩等比数列前项和的极限。
4． 了解数学归纳法的原理，并能用数学归纳法证明一些简单的问题。
[例题选讲]
[例1]等比数列
中，
且
是方程
的两根
（1）
求
的值；
（2）
求
的值。
[例2]等差数列的第10项为23，第25项为 -22，
（1） 求
；
（2） 求
的最大值；
（3） 若
，求
[例3]某林场的木材以每年25％的增长率逐年递增，但每年的砍伐量是
如果木材的原储量为
，从今年开始，计划在20年后使木材储量翻两番，求砍伐量的最大值
[能力训练]
一、选择题
1．在数列中，
则该数列中相邻两项乘积是负数的项是（ ）
（A）
和
（B）和
（C）和
（D）和
2．数列中，
，又数列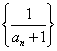
是等差数列，则
=（ ）
（A）0
（B）
（C）
（D）－1
3．在等差数中，若
则
等于（ ）
（A）90 （B）100 （C）110 （D）120
4．设是由正数组成的等比数列，公比
且
则
等于（ ）
（A）
（B）
（C）
（D）
5．等差数列共有
项，其中
则的值为（ ）
（A）3 （B）5 （C）7 （D）9
6．已知数列的首项
，又满足
则该数列的通项
等于（ ）
（A）
（B）
（C）
（D）
7．已知
顺次成等差数列，则（
）
（A）
有最大值，无最小值
（B）有最小值
，无最小值
（C）有最小值，最大值1 （D）有最小值 -1，最大值1
8．若 是等比数列，
且公比
为整数，则
=（ ）
（A）256 （B）-256 （C）512 （D）-512
9．已知
则
（ ）
（A）
（B）
（C）
（D）6
10．
的值为（
）
（A）2 （B）
（C）
（D）3
11．设是正项等比数列，且公比为，则
与
的大小关系为（ ）
（A）
（B）
（C）
（D）与公比的值有关
12．已知数列的通项公式
则=（ ）
（A）100 （B）50 （C）25 （D）125
二、填空题
13．在等差数列中，
则=_____.
14．在等比数列中，已知
则
_____________.
15．
_________________.
16．已知是一个首项为，公比为
的等比数列，且
则
_________________________________.
三、解答题
17．已知数列中，
且数列
是公比为的等比数列，数列
是公差为
的等差，求数列的通项公式。
18．用数学归纳法证明： 
19．在公差为
的等差数列和公比为的等比数列
中，已知
（1）求
的值；
（2）若存在常数
使
对一切自然数成立，求出的值；若不存在，说明理由。
（参考答案）
1~12. CBBBA BBCDA AB
13、10 14、4 15、
16、 
时，
；
时，
17、
18、
时，只要证
19、（1）
（2）