2005年 专题复习五 立体几何高考题型
热点之一:点、线、面问题
包括平面的基本性质、空间的直线和平面的位置关系及判定方法,特别注意三垂线定理及其逆定理的应用。
[例1] 已知![]() 是两个平面,直线
是两个平面,直线![]() 若以①
若以①![]() ,②
,②![]() ,③
,③![]() 中两个为条件,另一个为结论构成三个命题,则其中正确命题的个数是( )
中两个为条件,另一个为结论构成三个命题,则其中正确命题的个数是( )
(A)0个 (B)1个 (C)2个 (D)3个
[例2]把边长为![]() 的正方形剪去图中的阴影部分,沿图中
的正方形剪去图中的阴影部分,沿图中
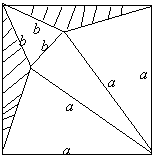 所画的线折成一个正三棱锥,则这个正三棱锥的高为( )
所画的线折成一个正三棱锥,则这个正三棱锥的高为( )
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
(练习)
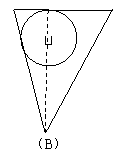
1.在一个倒置的正三棱锥容器内,放入一个钢球,钢球恰好与棱锥的四个面都接触,经过棱锥的一条侧棱和高作截面,正确的截面图形是( )
 |  | ||||||
 | |||||||
 | |||||||
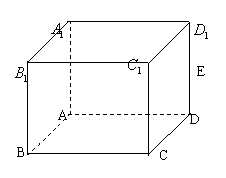 |
2.如右图,点E是正方体![]()
的棱![]() 的中点,则过点E与直线
的中点,则过点E与直线![]() 和
和
![]() 都相交的直线的条数是(
)
都相交的直线的条数是(
)
(A)0条 (B)1条 (C)2条 (D)无数
3.在正方体![]() 中,写出过顶
中,写出过顶
点A的一个平面______________,使该平面与正方体的12条棱所在的直线所成的角均相等(注:填上你认为正确的一个平面即可,不必考虑所有可能的情况)。
热点之二:空间角与距离问题
三个角:包括两条直线所成的角、直线与平面所成的角、二面角;
八个距离:包括点到直线的距离、点到面的距离、两条平行直线的距离、异面直线
的距离、直线与平行平面的距离、两个平行平面之间的距离、球面上两点的距离。
在求角或距离时,一定要“先找后解”。
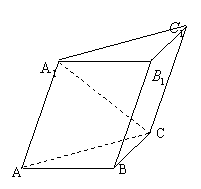 [例3](1998年全国高考题)已知斜三棱柱
[例3](1998年全国高考题)已知斜三棱柱![]() 的侧面
的侧面![]() 与底面
与底面![]() 垂直,
垂直,![]() ,
,
且![]()
(Ⅰ)求侧棱![]() 与底面
与底面![]() 所成角的大小;
所成角的大小;
(Ⅱ)求侧面![]() 与底面
与底面![]() 所成二面角的大小;
所成二面角的大小;
(Ⅲ)(理)求顶点C到侧面![]() 的距离;
的距离;
(Ⅲ)(文)求侧棱![]() 和侧面
和侧面![]() 的距离。
的距离。
(练习)
4.如图,在正方体![]() 中,E、F分别为
中,E、F分别为![]() 、
、![]() 的中点,
的中点,
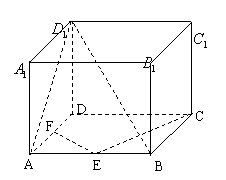 (1)
(1)![]() 与
与![]() 所成角的大小是_____________;
所成角的大小是_____________;
(2) ![]() 与
与![]() 所成角的大小是_____________;
所成角的大小是_____________;
(3) ![]() 与
与![]() 所成角的大小是_____________;
所成角的大小是_____________;
(4)![]() 与
与![]() 所成角的大小是_____________;
所成角的大小是_____________;
(5)![]() 与
与![]() 所成角大小是_____________;
所成角大小是_____________;
(6)![]() 与平面
与平面![]() 所成角的大小是_________;
所成角的大小是_________;
(7)![]() 与平面
与平面![]() 所成角的大小是_____________;
所成角的大小是_____________;
(8)二面角![]() 的大小是_________;
的大小是_________;
(9)二面角![]() 的大小是_____________;
的大小是_____________;
(10)二面角![]() 的大小是_____________;
的大小是_____________;
5.将锐角为60°,边长为![]() 的菱形
的菱形![]() 沿较短的对角线BD折成60°的二面角后,
沿较短的对角线BD折成60°的二面角后,
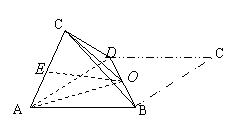 (1)求异面直线
(1)求异面直线![]() 与
与![]() 的距离;
的距离;
(2)求三棱锥![]() 的体积;
的体积;
(3)求D到面![]() 的距离。
的距离。
热点之三:表面积与体积问题
[例4]棱锥被平行于底面的平面所截,当截面分别平分侧棱、侧面积、体积时,相应截面面积记作![]() 、
、![]() 、
、![]() ,则( )
,则( )
(A)![]() (B)
(B)
![]()
 (C)
(C)![]() (D)
(D)![]()
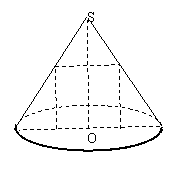
[例5]如右图,在母线长为2的等边圆锥内作一个内接圆柱,
当这个圆柱体积最大时,它的高是( )
(A)![]() (B)
(B) ![]() (C)
(C)![]() (D)
(D)![]()
 |
(练习)
6.如图,三棱台![]() 的上底
的上底![]() 面积
面积
为4,下底![]() 面积为9,且三棱锥
面积为9,且三棱锥![]() 的体
的体
积为9,则三棱台![]() 的体积为( )
的体积为( )
(A)19 (B)18 (C)![]() (D)
(D)![]()
7.已知圆台上、下底面半径分别为1cm和4cm,圆台的侧面展开图扇环所对的圆心角为216°,则该圆台的体积为_________________________。
8.直四棱柱![]() 的体积等于1,底面
的体积等于1,底面![]() 为平行四边形,则四面体
为平行四边形,则四面体![]() 体积为
体积为
____________。
热点之四:立几综合题
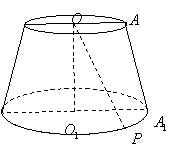 [例6]如图,圆台
[例6]如图,圆台![]() 的高等于下底面圆的半径,母线
的高等于下底面圆的半径,母线![]() 与下底面成
与下底面成![]() 的角,P为下底面圆周上的一点,
的角,P为下底面圆周上的一点,![]() 与
与![]() 成
成![]() 的角。
的角。
(Ⅰ)求二面角![]() 的余弦值;
的余弦值;
(Ⅱ)若下底面圆的半径为1,求圆台的侧面积。
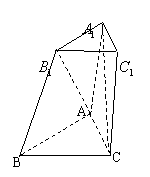
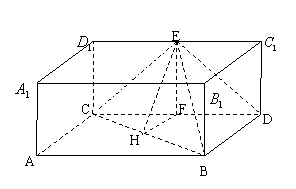 [例7]如图,直四棱柱
[例7]如图,直四棱柱![]() 的侧棱
的侧棱![]() 的长是a,底面ABCD是边长AB=2a,BC=a的矩形,E为
的长是a,底面ABCD是边长AB=2a,BC=a的矩形,E为![]() 的中点。
的中点。
(Ⅰ)求证:平面BCE⊥平面BDE;
(Ⅱ)求二面角E-BD-C的大小;
(Ⅲ)求三棱锥![]() 的体积.
的体积.
(练习答案)
1、B 2、B
3、面![]() 4、(1)
4、(1)![]() (2)
(2)![]() (3)
(3)![]() (4)
(4)![]() (5)
(5)![]() (6)
(6)![]() (7)
(7)![]() (8)
(8)![]() (9)
(9)![]() (10)
(10)![]()
5、(1)![]() (2)
(2)![]() (3)
(3)![]() 6、C 7、
6、C 7、![]() 8、
8、![]()