抛物线
1. 抛物线
上一点M到位点F的距离为
则该点纵坐标为（ ）
A. 
B. C.
D.
2. 若抛物线
上两点
关于直线
对称，则
，则
（ ）
A. 
B. 2 C.
D.
3
3. 过抛物线的焦点F的直线与抛物线相交于A、B两点，若A、B在抛物线准线上的射影为
，
。则
（ ）
A. 45° B. 60° C. 75° D. 90°
4. 已知抛物线
的焦点为F，定点
，在上取动点P，则
取最小值时，P点坐标为（ ）
A. 
B. 
C. 
D.
5. 抛物线
上有A、B、C三点横坐标依次为
, 2 , 3在
轴一点D纵坐标为6，则四边形ABCD为（ ）
A. 正方形 B. 菱形 C. 平行四边形 D. 任意四边形
6. 等边
内接于抛物线，
，则
（ ）
A. 3
B. 
C. 
D. 无法判断
7. 抛物线
的焦点F，准线
交
轴于R，过抛物线上一点
作
于
，则
（ ）
A. 12 B. 14 C. 16 D. 18
8. 抛物线
与椭圆
的公共弦长为（ ）
A. 1
B. 
C.
2
D.
9. 已知A、B是抛物线
上两点，0为原点，若
且
的重心恰为抛物线的焦点，则AB的直线方程为（ ）
A. 
B. 
C.
D. 
10. 抛物线
与直线
交于两点它们横坐标为
、
，直线与轴交点为
则,,
关系为（ ）
A. 
B. 
C. 
D. 
11. 已知动点
满足
则P点轨迹为（ ）
A. 抛物线 B. 直线 C. 双曲线 D. 椭圆
12. 两定点
，
动点P在抛物线上移动。则
重心G的轨迹方程为（ ）
A. 
B. 
C. 
D.
13. 抛物线上两定点A、B（A在轴上方，B在轴下方）F为焦点，
，
，P为抛物线AOB这一段上一点，求
面积最大值。
14. O为原点，A、B为抛物线上两点，并且
。
（1）求
最小值 （2）弦AB中点M到直线
距离最小值
15. 
为抛物线
内一点过A作直线交抛物线于P、Q，A恰为PQ中点求的方程。
16. A、B为抛物线上的两点，且（O为原点）求证：直线AB过定点。
【试题答案】
1. A 2. A 3. D 4. C 5. C 6. C 7. B
8. C 9. D 10. C 11. A 12. B
13. 由已知
准线
∴ 
∴ 
∴ 
∴ 
∴ 
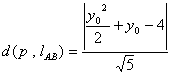
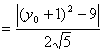
14. 解：
（1）
：
：
（2）
∴ 
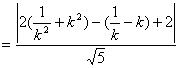
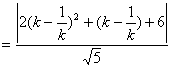
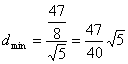
15. 解：设
∴ ：
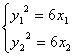
16. 证：设
：
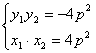
过定点
与解可设斜率为