高三数学周练试题(六)
一、选择题(每题5分共50分)
1.已知集合![]() ,
,![]() ,则
,则![]() =( )
=( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.“m=![]() ”是“直线(m+2)x+3my+1=0与直线(m-2)x+(m+2)y-3=0相互垂直”的( )
”是“直线(m+2)x+3my+1=0与直线(m-2)x+(m+2)y-3=0相互垂直”的( )
A.充分必要条件 B.充分而不必要条件 C.必要而不充分条件 D.既不充分也不必要条件
3.在![]() 的展开式中含有常数项,则正整数n的最小值是( )
的展开式中含有常数项,则正整数n的最小值是( )
A.4 B.5 C.6 D.7
4.已知直线m,n,平面![]() ,给出下列命题:
,给出下列命题:
①若![]() ;②若
;②若![]() ;③若
;③若![]() ;
;
④若异面直线m,n互相垂直,则存在过m的平面与n垂直.其中正确的命题是( )
A.②③ B.①③ C.②④ D.③④
5.一个幼儿园的母亲节联谊会上,有5个小孩分别给妈妈画了一幅画作为礼物,放在了5个相同的信封里,可是忘了做标记,现在妈妈们随机的任取一个信封,则恰好有两个妈妈拿到了自己孩子的画的概率为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.当![]() 时,函数
时,函数![]() 的最小值为( )
的最小值为( )
A.2
B.![]() C.4 D.
C.4 D.![]()
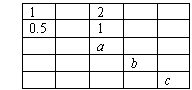 7.在如图的表格中,每格填上一个数字后,使每一横行成等差数列,每一纵行成等比数列,则a+b+c的值为( )
7.在如图的表格中,每格填上一个数字后,使每一横行成等差数列,每一纵行成等比数列,则a+b+c的值为( )
A.3 B.2 C.1 D.4
8. 已知两个正数![]() 满足
满足![]() ,则
,则![]() 取最小值时
取最小值时![]() 的值分别为 ( )
的值分别为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9. 已知点A(1,2),过点(5,-2)的直线与抛物线y2=4x交于另外两点B,C,那么△ABC是( )
A.锐角三角形 B.钝角三角形 C.直角三角形 D.答案不确定
10.已知![]() 为偶函数,且
为偶函数,且![]() ,当
,当![]() 时
时![]() ,若
,若![]() ,
,![]() 则
则![]() ( )
( )
A.2006
B.![]() C.
C.![]() D.
D.![]()
二、填空题(每题5分共30分)
11. 函数![]() 的单调减区间是
.
的单调减区间是
.
 12.经问卷调查,某班学生摄影分别执“喜欢”
12.经问卷调查,某班学生摄影分别执“喜欢”![]() “不喜欢”和“一般”三种态度,其中执“一般”态度的比“不喜欢”态度的多12人,按分层抽样方法从全班选出部分学生座谈摄影,如果选出的5位“喜欢”摄影的同学
“不喜欢”和“一般”三种态度,其中执“一般”态度的比“不喜欢”态度的多12人,按分层抽样方法从全班选出部分学生座谈摄影,如果选出的5位“喜欢”摄影的同学![]() 1位“不喜欢”摄影的同学和3位执“一般”态度的同学,那么全班学生中“喜欢”摄影的比全班人数的一半还多
人.
1位“不喜欢”摄影的同学和3位执“一般”态度的同学,那么全班学生中“喜欢”摄影的比全班人数的一半还多
人.
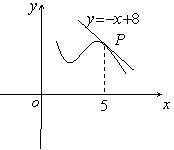
13. 如图,y=f(x)的图像在点P处的切线方程是![]() ,
,
则![]() +
+ ![]() =__________.
=__________.
14. 若![]() ,
,![]()
![]() ,且
,且![]() ,则向量
,则向量![]() 与
与![]()
的夹角为 .
15.设A、B、C是半径为R的球面上三点,AB、AC之间的球面距离为![]() ,BC间的球面距离为
,BC间的球面距离为
![]() ,则球心O到平面ABC的距离为
.
,则球心O到平面ABC的距离为
.
16.若函数![]() 的定义域为R,若存在常数
的定义域为R,若存在常数![]() ,使
,使![]() 对一切实数
对一切实数![]() 均成立,
均成立,
则称![]() 为有界泛函,给出下列函数:①
为有界泛函,给出下列函数:①![]() ;②
;②![]() ;③
;③![]() ;
;
④![]() ;⑤
;⑤![]() 是定义域在R上的奇函数,且满足对一切实数
是定义域在R上的奇函数,且满足对一切实数![]() ,
,![]() 均
均
![]() ;其中是有界泛函的序号为
.
;其中是有界泛函的序号为
.
高三数学周练试题(六)
班级_______________ 姓名_________________ 学号________
一、选择题:(每小题5分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
二、填空题:(每小题5分)
11、 12、 13、 14、
15、 16、
三、解答题: (每小题14分,共5题)
17.已知函数 ![]()
(1)求函数![]() 的最小正周期
的最小正周期![]() ;
;
 (2)若函数
(2)若函数![]() 在[-
在[-![]() ,
,![]() ]上的最大值与最小值之和为
]上的最大值与最小值之和为![]() ,求出
,求出![]() 并画出函数在
并画出函数在![]() 的图象.
的图象.
18.某外商到一开发区投资72万美元建起一座蔬菜加工厂,第一年各种经费12万美元,以后每年增加4万美元,每年销售蔬菜收入50万美元。设![]() 表示前n年的纯收入(
表示前n年的纯收入(![]() 前n年的总收入-前n年的总支出-投资额).
前n年的总收入-前n年的总支出-投资额).
(1)从第几年开始获取纯利润?
(2)若干年后,外商为开始新项目,有两种处理方案:①年平均利润最大时以48万美元出售该厂;②纯利润总和最大时,以16万元出售该厂,问哪种方案最合算?
19.如图,正方形A1BA2C的边长为4,D是A1B的中点,E是BA2上的点,将△A1DC及△A2EC分别沿DC和EC折起,使A1A2重合于A,且二面角A—DC—E为直二面角.
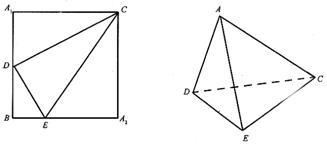 (1)求证:CD⊥DE;
(1)求证:CD⊥DE;
(2)求AE与面DEC所成角的正弦值;
(3)求点D到平面AEC的距离.
20.一条斜率为1的直线![]() 与离心率为
与离心率为![]() 的椭圆
的椭圆![]() :
:![]() (
(![]() )交于P、Q,两点,直线
)交于P、Q,两点,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,且
,且![]() ,
,![]() .
.
(1)求直线![]() 和椭圆
和椭圆![]() 的方程;
的方程;
(2)若![]() ,其中
,其中![]() 是坐标原点,求
是坐标原点,求![]() 值.
值.
21. 已知定义域为R的二次函数![]() 的最小值为0且有
的最小值为0且有![]() ,直线
,直线![]() 被
被![]() 的图像截得的弦长为
的图像截得的弦长为![]() ,数列
,数列![]() 满足
满足![]() ,
,![]() .
.
(1)求函数![]() ;
;
(2)求数列![]() 的通项公式;
的通项公式;
(3)设![]() ,求数列
,求数列![]() 的最值及相应的n.
的最值及相应的n.