高三数学综合练习三
一、选择题（每小题5分，共60分）
1、已知全集U=R，集合A={xx2>4}，B={xx2-6≤0}，则Cu(A∪B)=（ ）
A
{xx<－3} B {x－2≤x≤2} C R D 
2、已知：函数f(x)=2x+
是奇函数，下列函数中，在（0，2）上为减函数的是（ ）
A y=x2+2ax－1 B y=log1-ax
C
y=－ax3－12x+1 D
y=x－
3、设等比数列{an}的前n项和为Sn，若S6：S3=1：2，则S9：S3=（ ）
A 1：2 B 2：3 C 3：4 D 1：3
4、sin1630sin430－sin730sin470=( )
A
B 
C 
D 
5、向量
=（4，n）共线且反向，则n=( )
A ±2 B －2 C 2 D 0
6、关于x的方程7x=
有正根，则a的取值范围是（ ）
A （7，+∞） ∪（－∞，1） B （1，+∞）
C （－5，1） D （1，7）
7、a=－1是方程“a2x2+(a+2)y2+2ax+a=0表示圆”的（ ）
A 充要条件 B 充分不必要条件
C 必要不充分条件 D 既非充分又非必要条件
y≤x
8、已知：x,y满足不等式组 x+2y≤4,则t=(x+1)2+(y－1)2的最小
y≥－2
值是（ ）
A 
B 2 C 3 D 
9、若函数y=x2－3x－4的定义域是[0，m]，值域是[－
，则m的取值范围是（ ）
A （0，4] B [
C [
D （
∞）
10、有3对夫妻共6人，排成一行，要求同一对夫妻都不能相邻，则不同的排法有（ ）
A 720 B 432 C 360 D 240
11、直线
是双曲线
）的右准线，以原点为圆心且过双曲线顶点的圆，被分成弧长为2：1的两段圆弧，则离心率是（ ）
A 2 B C 
D 
12、若方程m(x2+y2+2y+1)=(x－2y+3)2表示椭圆，则m的取值范围是（ ）
A （0，1） B （1，+∞） C （0，5） D （5，+∞）
二、填空（每小题4分，共24分）
13、已知：
14、（
的展开式中，x2的系数是__________。
15、求和：
。
16、已知：θ∈R，且sinθ=1+cosθ,则cot
17、设a,b都是正实数，且2a+b=1，设T=
，则T的最大值是_________。
18、给出四个命题：
①函数f(x)=xx+bx+c为奇函数的充要条件是c=0
②函数y=2-x(x>0)的反函数是y=－log
③若函数f(x)=lg(x2+ax－a)的值域是R，则a≤－4或a≥0
④y=f(x－1)是偶函数，则y=f(x)关于x=0对称
所有正确命题的序号是__________。
高三数学综合练习三
班级__________ 姓名____________ 学号_______
一、选择题
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
二、填空题
13、___________ 14、__________ 15、___________
16、___________ 17、__________ 18、___________
三、解答题
19、已知：
，求：
20、数列{an}中，a1=8,a4=2，且满足an+2-2an+1+an=0,
(1)求：数列{an}的通项公式
（2）Sn=a1+a2+…+an，求：Sn
（3）bn=
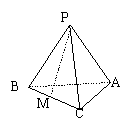21、三棱锥P-ABC中，面PBC⊥面ABC，△PBC是边长为1的正三角形，∠ACB=900，∠BAC=300，M是BC的中点。
（1）求证：PB⊥AC
（2）求：M到面PAC的距离
（3）求二面角C-PA-M的正弦值
22、双曲线C1:x2－y2=1，抛物线C2:x2=2y，点P是抛物线C2上的点，直线过点P并与抛物线C2在点P的切线垂直，直线与抛物线C2交于另一点Q，直线与双曲线C1交于两点K、T。
（1）若P的横坐标为2，求：PQ
（2）是否存在P，使
23、已知：函数f(x)=
恒成立
（1）求：P的取值范围
（2）若x<0时，f(x)<1也恒成立，求：p值
（3）在（2）的条件下，求使不等式
对唯一的一个整数k成立的最大正整数n，并求k值。