高三数学综合练习四
一、选择题
1、集合A={1,2,3}，B={－1,0,1}，满足f(3)=f(1)+f(2)的映射f:A→B的个数（ ）
A 2 B 4 C 5 D 7
2、已知点（2，1）和（－3，2）在直线3x－2y+a=0的同侧，则a的取值范围是（ ）
A －4<a<13 B －13<a<4 C a<－4或a>13 D a<－13或a>4
3、在△ABC中，“A>300”是“sinA>
”的（ ）
A 充分而不必要条件 B 必要而不充分条件
C 充分必要条件 D 既不充分也不必要条件
4、在平面直角坐标系中，O为坐标原点，
=（1，0），P为平面内动点，若
=
，则P点的轨迹是（ ）
A 圆 B 椭圆 C双曲线 D 抛物线
5、已知二项式
的展开式中含x
的项是第8项，则二项式系数最大的项是（ ）
A 第15，16项 B 第14，15项 C 第15项 D第16项
6、 如图，在正三棱锥P—ABC中，E、F分别是PA、AB的中点，∠CEF=900，
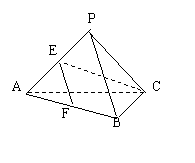若AB=a，则该三棱锥的全面积为（ ）
A 
B 
C 
D 
7、自行车车轮直径为28英寸，从车轮外缘点A在最低位时算起，自行车前进了
英寸，则此时点A离地的高度为（ ）
A 7英寸 B 14英寸 C
21英寸 D （14+7
）英寸
8、已知二次函数f(x)=x2+x+a(a>0)，若f(m)<0，则f(m+1)的值（ ）
A 正数 B 负数 C 零 D 符号与a有关
9、定义在R上的函数f(x)的最小正周期为T，若函数y=f(x)，在x∈(0, T)时有反函数y=f-1(x)，x∈D,则函数y=f(x)，在x∈(2T,3T)的反函数是（ ）
A y=f-1(x),x∈D B y=f-1(x+2T),x∈D
C y=f-1(x)+3T,x∈D D y=f-1(x)+2T,x∈D
10、已知F1、F2为椭圆E的左、右焦点，抛物线C以F1为顶点，F2为焦点，设P为椭圆与抛物线的一个交点，如果椭圆E的离心率e满足等式PF1=ePF2，则e值是（ ）
A 
B 
C 
D 
二、填空题
11、在一组数据：
，它们的算术平均值为20，若去掉其中的
，余下数据的算术平均值为18，则关于
的表达式为________.
12、已知
且
，那么
________.
13、函数
的值域为__________,
14、已知
且
的夹角为锐角，则
的取值范围是________.
15、若把英语单词“error”中字母的拼写顺序写错了，则可能出现的错误的种数为_________.
16、删去正整数数列1、2、3、4……中所有能被100整除的数，得到一个新数列，则这个新数列的第2004项是_________.
高三数学综合练习四
班级__________ 姓名____________ 学号_______
一、选择题
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
二、填空题
11、___________ 12、___________ 13、___________
14、___________ 15、___________ 16、__________
三、解答题
17、已知函数
（其中
）的图象在
轴右侧的第一个最高点为
，与轴在原点右侧的第一个交点为
，
（1） 求这个函数的解析式；
（2） 此函数可由
经过怎样的变换得到？（写出一个具体的变换）
18、一次数学测验共10道选择题，每题都有四个选择支，其中有且只有一个是正确的。考生要求选出其中正确的选择支，只准选一个选择支。评分标准规定：答对一题得4分，不答或答错一题倒扣1分。
某考生确定有6道题是解答正确的；有3道题的各四个选择支中可确定有1个不正确，因此该考生从余下的三个选择支中各题分别猜选一个做答；另外有1题因为题目根本读不懂，只好乱猜。在上述情况下，试问：
（1）该考生这次测试得分为20分的概率；
（2）该考生这次测试得分为30分的概率.
19、设函数
（1） 试确定
和
的单调区间及相应区间上的单调性；
（2） 说明方程
是否有解，并对自然数，给出关于的方程
无解的一个一般结论，加以证明。
20、如图正方体
的棱长为1，
点是棱
上的一点且
，
（1） 
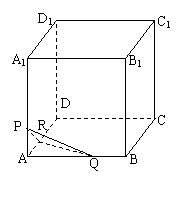经过点截去正方体的一个角，使得截面
与底面所成的二面角为
时，求三棱锥
体积的最小值；
（2） 试确定
的位置，使得截面
21、已知函数
设正项数列
的首项
，前项和
，数列
的前项和
且
（1） 求
的表达式；
（2） 在直角坐标系内，直线
的斜率为
，且与曲线
有且仅有一个交点，与轴交于
，设
，求
；
（3） 在（2）的条件下，若
，求证：
22、如图：过抛物线
的对称轴上任一点
作直线与抛物线交于
两点（A为右交点），点Q是点P关于原点的对称点.
（1） 设点P分有向线段
所成的比为
.证明：
；
（2） 
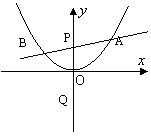设直线AB的方程是
，过A、B两点的圆C与抛物线在点A处有共同的切线，求圆C的方程.