高三年级综合考试数学试题
一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一个是符合题目要求的.
1. 设集合![]() 则
则![]() ∪
∪![]() 等于 ( )
等于 ( )
A.![]() B.
B.
![]() C.
C. ![]() D.
D.
![]()
2. 不等式![]() 的解集为 ( )
的解集为 ( )
A. ![]() B.
B. ![]() ∪
∪![]()
C. ![]() ∪
∪![]() D.
D. ![]() ∪
∪![]()
3.用数字0,1,2,4,5组成无重复数字的三位数,其中偶数有 ( )
A.24个 B. 30个 C. 40个 D. 60个
4.函数![]() ( )
( )
A.在![]() 内单调递增
B. 在
内单调递增
B. 在![]() 内单调递减
内单调递减
C.在![]() 内单调递增 D. 在
内单调递增 D. 在![]() 内单调递减
内单调递减
5.等差数列![]() 中,已知
中,已知![]() ,则
,则![]() 等于 ( )
等于 ( )
A.2:1 B. 3:1 C. 4:1 D. 8:1
6.已知函数![]() =
=![]() 图象上相邻的一个最大值点和最小值点恰好都在曲线
图象上相邻的一个最大值点和最小值点恰好都在曲线![]() 上,则函数
上,则函数![]() 的最小正周期为 ( )
的最小正周期为 ( )
A.1 B. 2 C. 3 D. 4
7. 直角三角形![]() 的三边长分别为6,8,10,则到三个顶点
的三边长分别为6,8,10,则到三个顶点![]() 、
、![]() 、
、![]() 距离都为3的平面有且仅有 ( )
距离都为3的平面有且仅有 ( )
A.2个 B. 3个 C. 5个 D. 7个
8.设函数![]() ),
),![]() 的最小值为
的最小值为![]() 的最大值为
的最大值为![]() ,设
,设![]() ,则数列
,则数列![]() ( )
( )
A.是公差不为0的等差数列 B. 是公比不为1的公比数列
C. 是常数列 D. 不是等差数列也不是等比数列
9.一条光线从点![]() 出发,射到直线
出发,射到直线![]() 上的
上的![]() 点,光线经此直接反射后又射到
点,光线经此直接反射后又射到![]() 轴上的C点,设
轴上的C点,设![]() ,若
,若![]() ,则
,则![]() 的取值范围是( )
的取值范围是( )
A.![]() B.
B. ![]() C.
C.
![]() D.
(1,3)
D.
(1,3)
10. 某种商品的进货规则是:若进货不超过50件,则每件![]() 元,若超过50件,则每件为
元,若超过50件,则每件为![]() 元. 现进货不超过50件,共花了
元. 现进货不超过50件,共花了![]() 元,若多进11件,则花费仍是
元,若多进11件,则花费仍是![]() 元.设每件进货价都是整数元,则
元.设每件进货价都是整数元,则![]() 等于
( )
等于
( )
A. 1980 B. 3690 C. 6600 D. 7200
二、填空题:本大题共6小题,每小题5分,共30分.
11.已知![]() 展开式中的常数项为
展开式中的常数项为![]() ,则
,则![]() 的值为_______.
的值为_______.
12. 甲、乙两人进行五盘三胜制的象棋赛,若甲每盘获胜的概率为![]() ,乙每盘获胜的概率为
,乙每盘获胜的概率为![]() ,则比赛以甲比乙为3比1获胜的概率为______.
,则比赛以甲比乙为3比1获胜的概率为______.
13.坐标平面内,点![]() 与两个定点
与两个定点![]() 连线的斜率之积为常数
连线的斜率之积为常数![]() ,当
,当![]() 点轨迹是一条准线方程为
点轨迹是一条准线方程为![]() 的双曲线时,
的双曲线时,![]() 的值为______.
的值为______.
14. 给出下列四个命题
①过平面外一点作与该平面成![]() 角的直线一定有无穷多条;
角的直线一定有无穷多条;
②一条直线与两个相交平面都平行,则它与这两个平面的交线平行;
③对确定的两条异面直线,过空间任意一点有且只有一个平面与这两条异面直线都平行;
④对确定的两条异面直线,都存在无穷多个平面与这两条异面直线所成的角相等.
其中正确命题的序号是__________.
15.实数![]() 、
、![]() 满足不等式组
满足不等式组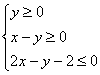 ,则
,则![]() 的取值范围是_____.
的取值范围是_____.
16. 已知![]() ,则
,则![]() 的最小值为_______.
的最小值为_______.
高三年级综合考试数学试题
答题纸
一、选择题(每小题5分,共50分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
二、填空题(每小题5分,共30分)
11. 12. 13.
14. 15. 16.
三、解答题:本大题共5小题,共70分.解答应写出文字说明,证明过程或演算步骤.
17. (本小题满分12分)
已知![]()
![]() ,且
,且![]()
(1)求![]() 与
与![]() 的夹角;
的夹角;
(2)若![]()
![]() ,且
,且![]() ,求
,求![]() .
.
18. (本小题满分14分)
已知函数![]()
(1)若直线![]() 是函数
是函数![]() 图象的切线,求
图象的切线,求![]() 的值;
的值;
(2)若函数![]() 在[1,2]上是减函数,在[3,4]上是增函数,求实数
在[1,2]上是减函数,在[3,4]上是增函数,求实数![]() 的取值范围.
的取值范围.
19. (本小题满分14分)
已知正三棱柱![]() 的每条棱长都为
的每条棱长都为![]() ,
,![]() 为棱
为棱![]() 上的动点.
上的动点.
(1)求三棱锥![]() 体积的最大值.
体积的最大值.
(2)当![]() 在何处时,
在何处时,![]() 平面
平面![]() ,并证明之;
,并证明之;
(3)在(2)的条件下,求平面![]() 与平面
与平面![]() 所成锐二面角的大小.
所成锐二面角的大小.
20. (本小题满分15分)
已知函数![]() 在
在![]() 上有意义,
上有意义,![]() ,且满足
,且满足![]() 、
、![]()
![]() 时,有
时,有![]() )
)
(1)证明![]() 在
在![]() 上是奇函数;
上是奇函数;
(2)对数列![]() ,
,![]() ,求
,求![]() ;
;
(3)对于(2)中的数列![]() ,求证:
,求证:![]()
![]() …
…![]()
![]() .
.
21.(本小题满分15分)
已知椭圆![]() ,
,![]() 为其左、右焦点,
为其左、右焦点,![]() 为右顶点,
为右顶点,![]() 为左准线,过
为左准线,过![]() 的直线
的直线![]() (
(![]() )与椭圆相交于
)与椭圆相交于![]() ,
,![]() 两点,且有
两点,且有![]() .
.
(1)若![]() ∩
∩![]()
![]()
![]() ∩
∩![]() =
=![]() ,求证:
,求证:![]() 两点的纵坐标之积为定值;
两点的纵坐标之积为定值;
(2)求椭圆![]() 的离心率的最小值;
的离心率的最小值;
(3)若![]() ),求
),求![]() 的范围.
的范围.