高三年级综合考试数学试题
一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，
只有一项是符合题目要求的．
1．命题“若A∪B=A,则A∩B=B”的否命题为
A.若A∪B≠A,则A∩B≠B B. 若A∩B=B,则 A∪B=A
C.若 A∩B≠B,则A∪B≠A D. 若A∪B≠A则A∩B=B
2. 已知
=（－1，1）,
=（2，0）,则与的夹角等于
A.300 B.600 C.900 D.1350
3. 过点
作直线
与圆
交于A、B两点，若
，则
A．的方程为
；
B．的方程为
；
C．的方程为
；
D．的方程为
.
4. 设
，
，
，则a、b、c的大小关系是
A．
B．
C．
D．
5. 不等式
的解集为
A．
B．
C．
D．
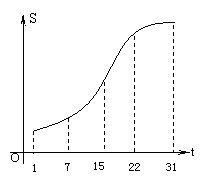6. 某地发生禽流感，从1月1日到31日累计死亡的鸡的数量S与时间t的关系如图所示，给出下列说法：
（1）31日该地几乎没有鸡死亡
（2）1月15日死亡的鸡估计最多
（3）22日—31日期间死亡的鸡比15日—22日
期间死亡的鸡多
（4）这个月期间，月初鸡的日死亡数量少，月中
前后鸡的日死亡数量多，月末鸡的日死亡数量又变少
其中正确的说法有
A.（1）（2）（3） B.（1）（2）（4） C.（1）（3）（4） D.（2）（3）（4）
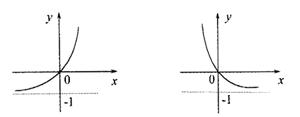
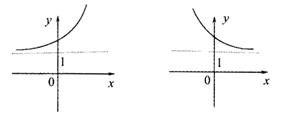7. 函数
的反函数图像是
A B C D
8.球面上有三点，其中任意两点的球面距离都等于球的大圆周长的
，经过这三点的小圆的周长为
，则这个球的表面积为
A．
B．
C．
D．
9. 使可行域为 的目标函数
，在
= 2, 
= 2取得最大值的充要条件是
A. 
≤
B. ≤ C.≥ D.≥
10. 已知
，则
在
处的导函数值
为
A 
B 
C.
D.
11. 若一系列函数的解析式相同，值域相同，但定义域不同，则称这些函数为“朋友函数”，那么函数解析式为
，值域为
的“朋友函数”共有
A．7个 B．8个 C．9个 D．10个
12
电子计算机使用二进制（只有两个数码0 1，逢2进一），它与十进制的换算关系如下表：
| 十进制数 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | … |
| 二进制数 | 0 | 1 | 10 | 11 | 100 | 101 | 110 | 111 | 1000 | 1001 | 1010 | … |
观察二进制为1位数 2位数 3位数时，对应的十进制的数 当二进制为6位数时，能表示十进制中最大和最小的数分别为
A 63，32 B 63，31 C 64，32 D 64，31
二、填空题：本大题共6小题，每小题4分，共24分.将答案填在题卡相应的位置.
13．对甲乙两学生的成绩进行抽样分析，各抽取5门功课，得到的观测值如下：
甲：70 80 60 70 90 乙：80 60 70 84 76
那么，两人中各门功课发展较平稳的是 ．
14．若
，
，
成等差数列，，
，
成等比数列，则实数的值为
.
15．过抛物线
上一点
作倾斜角互补的两条直线
、
交抛物线于
、
两点，则直线
的斜率为_____________．
16．设命题
:
和命题
:对任何∈R，
，若和有且仅有一个成立，则实数
的取值范围是____________．
17．由等式
定义映射
.
18. 设有四个条件：
①平面
与平面
、
所成的锐角二面角相等；
②直线a∥b，a⊥平面，b⊥平面；
③a、b是异面直线，
，且a∥，b//；
④平面内距离为d的两条平行直线在平面内的射影仍为两条距离为d的平行线.
其中能推出//的条件有 .（填写所有正确条件的代号）
三、解答题：本大题共5小题，共66分.解答应写出必要的文字说明，证明过程或演算步骤.
19．（本小题满分12分）已知函数=
ω·cosω-cos2ω(ω＞0)的周期为
.
(1)求ω的值；
(2)△ABC的三边、、满足
，且边所对的角为，求此时函数的值域.
20. （本小题满分12分）据报道，中国成功发射载人飞船“神州6号”的火箭“长征2号F”发射的可靠性达到0.97，安全性达到0.997，（可靠性指火箭能成功发射的概率，安全性指火箭发射不成功时，航天员能成功逃逸的概率），则
（1）求这次中国发射载人飞船时，航天员安全的概率.
（2）若从飞船中带回的植物种子每粒成功发芽的概率都为
，假定某次实验种子发芽则称该次实验是成功的，如果种子没有发芽，则称该次实验是失败的.某工作小组做了三次实验，求至少两次实验成功的概率.
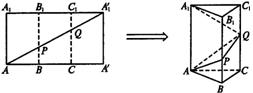21.（本小题满分14分）如图，将长AA′=3
，宽AA1=3的矩形沿长的三等分线处折叠成一个三棱柱，如图所示：
(1)求平面APQ与底面ABC所成的锐二面角的正切值；
(2)求三棱锥A1—APQ的体积；
（3）求C1到平面APQ的距离.
22.（本小题满分14分）已知数列{an}中，a1>0, 且an+1=
，
(1)试求a1的值，使得数列{an}是一个常数数列；
(2)试求a1的取值范围,使得an+1>an对任何正整数n都成立；
(3)若a1 = 2，设bn = an+1－an (n = 1，2，3，…)，并以Sn表示数列{bn}的前n项的和，求证：Sn<
．
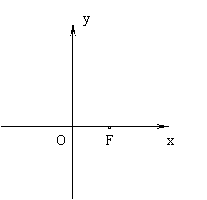
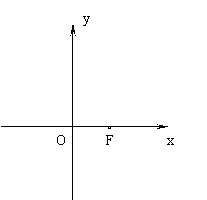
23.（本小题满分14分）以O为原点，
所在直线为轴，建立如图所示的直角坐标系.设·
=1，点F的坐标为(
，0)，∈[3，+∞)，点G的坐标为(
，
).
(1)求关于的函数=
的表达式，判断函数的单调性，并证明你的判断；
(2)设△OFG的面积
，若以O为中心，F为焦点的椭圆经过点G，求当
取得最小值时椭圆的方程；
(3)在(2)的条件下，若点P的坐标为(0，
)，C、D是椭圆上的两点，且
=λ
(λ≠1)，求实数λ的取值范围.
高三年级综合考试数学试题
答题纸
一、选择题：
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
二、填空题：
13、 14、 15、
16、 17、 18、
三、解答题：本大题共5小题，共66分.解答应写出文字说明，证明过程或演算步骤.
19．（本小题满分12分）
20. （本小题满分12分）
21. （本小题满分14分）
|
|
座位号
22. （本小题满分14分）
23. （本小题满分14分）
|
|
