高三数学辅导练习(立体几何)

高三数学辅导练习(立体几何)

1、若a、b为直线，α为平面，下列命题中不成立的是（　 ）

（A）若a∥b, a⊥α, 则b⊥α　　 （B）a⊥α, b⊥α,则a∥b

（C）若a⊥α，bα，则a⊥b　　(D)若a⊥b，a⊥α，则b∥α

2、长方体ABCD—A₁B₁C_1­D₁中AB=15,BC=8, 则AA₁与平面BB₁DD₁的距离为（　 ）

 (A)　　　　　 (B)　　　　　　(C)8　　　　　　 (D)15

3、设PA为平面α的一条斜线，AC在平面α内，P到平面α的距离为1，PA=2，则∠PAC的范围是（　 ）

 A、θ30°　　B、θ30°　　C、30°θ150°　　D、30°θ180°

4、P是△ABC所在平面外一点，且PA、PB、PC与平面α所成的角相等，则P在平面α内的射影是△ABC的（　 ）

  A、外心　　　　B、内心　　　　C、重心　　　　 D、垂心

5、若mα，α⊥β，m⊥β，则直线m与平面α的关系是　（　 ）

　　（A）平行　　　（B）相交　　　（C）垂直　　　（D）以上均不对

6、不重合的两直线a，b及三个平面α、β、γ具备下列哪个条件时b⊥α　（　 ）

　　（A）a⊥b,　bα　　　　　　 （B）α⊥β, α∩β=b, αβ, a⊥b

　　（C）a⊥γ, αγ　　　　　  （D）α⊥β, βγ=a

7、有一山坡，倾斜度为30°，若在斜坡平面上沿着一条与斜坡底线成45°角的直线前进1公里，则升高了　 （　 ）

　 （A）250米　　（B）250米　　（C）250米　　（D）500米

8、在地球北纬圈上有A、B两点,它们的经度相差,则A 、B两点沿纬度圈的弧长与A 、B两点间的球面距离之比是 (　　)

（A）3∶2　　　　　（B）2∶3　　　 （C）1∶3　　　 （D）3∶1

9、正四面体内切球的球心到一个面的距离等于这个四面体的高　 (　　)

（A）1/4　　　　　 （B）1/3　　　　 （C）　1/2　　　（D）/6

10、E是边长为4的正三角形ABC的AB边上的中点，AD⊥BC于D，把△ABC沿AD折成60°的二面角B—AD—C，则CE等于　　（　 ）

　 （A）　　　　 （B）　　　 （C）2　　　 （D）6

11、△ABC的三边形为3，4，5，P 为平面ABC外一点，它到三边的距离都等于2，则P到平面α的距离为 　　　 .

12、是平面α内的直线，A是α外的一点，设A到α的距离为d₁,A到的距离为d₂，则d₁、d₂的大小关系是　　　　 .

13、已知A、B两点到平面α的距离分别是4、1，AB与α所成角为60°，则线段AB在

α上的射影长为　　　　 .

14、已知E、F分别是边长为2的正方形ABCD的边AB、CD的中点，沿EF将其折成二面角，这时AC=，则二面角A—EF—C的度数为______.

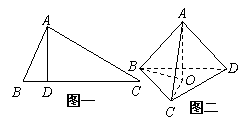15、如图一，在△中，、，是垂足，则（射影定理）.类似有命题：三棱锥(图二)中，⊥平面，⊥平面，为垂足，且在△内，则，上述命题是　 （　　）

  　A．真命题　　　　B．假命题

　　C．增加“”的条件才是真命题

　　D．增加“三棱锥是正三棱锥”的条件才是

真命题

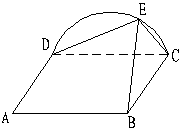
16、如图，四边形ABCD为矩形，E在以CD为直径的半圆上，平面ABCD⊥平面DCE，AD=DE=a，AB=2a，求（1）AD与BE所成角，（2）二面角E—AB—C的正切值。

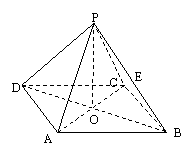
17、如图所示,正四棱锥中，侧棱与底面所成的角的正切值为.

（1）求侧面与底面所成的二面角的大小；

（2）若是的中点，求异面直线与所成角的正切值；

（3）在侧面上寻找一点，使⊥侧面，试确定点的位置，并加以证明．