高三数学回味练习二
1. 
是
成立的（ ）
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要
2. 若函数
,则
( )
A. 是偶函数，有最大值 B. 无奇偶性，有最大、最小值
C. 是偶函数，有最小值 D. 无奇偶性，值域是实数集
3．抛物线
与抛物线
关于直线
对称，则的准线方程为（ ）
A．
B.
C.
D. 
4．已知函数
若对任意
，都有
，则
）的值为（ ）
A．0 B.
3 C.
D.
3或
5．若点
动点
满足
，则
的最小值是 A．
B.
1 C. 
D. 2
（ ）
6．设实数
满足
，则
与
的大小关系为（ ）
A. 
B.
C. 
D.
不能确定，它们的大小与
有关
7．在直角三角形
中，
，那么
（ ）
A．有最大值
和最小值 B.
有最大值但无最小值
C. 既无最大值也无最小值 D.
有最大值
但无最小值
8. 若是双曲线
的右支上的动点，
是双曲线的右焦点，已知
，则
的最小值为
（ ）
A. 
B.
C.
3
D. 
9．已知
，直线
与曲线
交于
两点，则
是原点）的面积等于（ ）
A. 
B. 
C. 
D. 
10. 设集合
，且集合
为单元素集合，则实数的取值范围为（ ）
A. 
B.
或
C. 
D.
或
11．已知直线
、
和平面
，那么
的一个必要但非充分的条件是（ ）
A. 
B 
C． 
且
D.
、与成等角
12. 命题
及点
满足
，命题
是
的重心.
则
是
的（ ）
A. 充分非必要条件 B. 必要非充分条件
C. 充分必要条件 D. 既非充分又非必要条件
13．
是对于[0，1]上的一切
值，
恒成立的（ ）
A. 充分非必要条件 B. 必要非充分条件
C. 充要条件 D. 既不是充分条件，也不是必要条件
14. 不等式组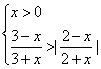
的解集是（ ）
A. 
B.
C. 
D.
15．双曲线
的半焦距为
，顶
到渐近线的距离为
，则双曲线的离心率为（ ）
A. 
B.
3
D 或
D.
或3
16．已知
是空间四条直线，如果
，那么（ ）
A. 
且
B.
中任两条都不平行
C. 或 D.
至多有一对直线平行
17．已知
），双曲线
上一点
到
的距离为11，
是
的中点，O为坐标原点，则
（ ）
A. 
B.
C.
D.或
18．“
或2”是方程“
表示圆”的（ ）
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既非充分又非必要条件
19．若实数
成等差数列，实数
成等比数列，则
的取值范围是（ ）
A. 
B.
C．
D.
20．函数
在区间
上是单调增函数，则的取值范围是（ ）
A. B. 
C.
D. 
21．直线
，直线
与两坐标轴正向围成的四边形有一个外接圆，则
的值为（ ）
A. 
B.
1 C. 2 D.
22．有四个函数：①
，②
，③
④
其中，周期
，且在
上是增函数的函数的个数是（ ）
A. 1 B. 2 C. 3 D. 4
23．双曲线
的一个焦点是
，则的值为（ ）
A. B.
1 C. 
D. 
24. 如图，长方体
中，
，
，那么异面直线
与
所成角的大小是（ ）
A.
arcsin
B. 
C .
D. 
25. 函数
与函数
图象关于（ ）
A. 轴对称 B.
轴对称
C． 直线
对称 D.
直线
对称
26．设是
上以2为周期的奇函数，已知当
时，
，那么在(1,2)上是（ ）
A. 增函数且
B.
增函数且
C. 减函数且 D.
减函数且
27．双曲线
的一条准线被两渐近线截得的线段长等于一个焦点到一条渐近线的距离，则双曲线的两条渐近线的斜率为（ ）
A. 
B.
C.
D.
28. 三棱锥
的三个侧面两两垂直，
若
四个点都在同一球面上，则此球面上
两点之间的球面距离是（ ）
A．
B. 
C.
D.
29. 若两直线
与
平行，则的值为（ ）
A. B. 2
C. 和2
D. 0和1
30．若是偶函数，且当
时，
则
的解集是（ ）
A．
B.
或
C． D.
31．设直线
，则
到
的角为（ ）
A. 
B.
C.
D.
32．“
”是“
和
的夹角是钝角”的（ ）
A．必要非充分条件 B. 充分非必要条件
C. 充要条件 D. 既不充分也不必要条件
33. 有5个座位连成一排，现安排3个人就座，则有两个空位不相连的不同坐法共有 A．28种 B. 36种 C. 60种 D. 72种 （ ）
34．编号为1，2，3，4，5的5个人，分别坐在编号为1，2，3，4，5的座位上，则至多有两个号码一致的坐法有_______种.
35．设直平行六面体
中，
互相垂直，且
，则点
到平面
的距离为_______.
36．两个四位数
各位上的数字是从1，2，3，4，5，6中选取（可重复），且
，则实数对（）表示平面上不同点的个数为_______.
37．已知三棱锥的三条侧棱长均为1，且两两互相垂直，若该三棱锥的四个顶点都在同一个球面上，则这个球的表面积是_______.16.
，则________.
38. 设集合
若
，则实数的取值范围为_______.17．关于直线和平面
，有以下四个命题：
（1）当
时，
（2）当
时，
（3）当
时，
且
（4）当
或
其中假命题的序号是：_____________.
39．若无论实数
取何值、关于的不等式
的解集是空集，则
的取值范围是_________.
40．设集合
，映射
满足
，则映射
的个数为_______.
41．用1，2，3三个数字排成一个四位数，每个数字都排上，所得四位数的个数为______.
42.对于给定的函数
，有下列四个结论：
(1)的图象关于原点对称；
(2)在上是增函数；
(3) 
；
(4) 
有最小值0.
其中正确结论的序号是____________.
43.已知等差数列
的前项和为
，且
，则过点（
的直线的斜率为_______.
44. 若A为的内角，则
的取值范围是_________.
45．从5名男生、6名女生中各选4名，男女相间排列的方法共有_______种.
46．如果函数
在
上单调递增，则的范围
47. 已知
若
，则使函数为偶函数的
值为________.
48. 设
，从A到B的映射，使B中的每一个元素都有A中元素与之对应，这样的映射共有______个.
49．某校准备参加2004年全国高中数学联赛，把10个选手名额分配到高三年级的3个班，每班至少一个名额，则不同的名额分配方案有______种.
50．若圆
上有且仅有两个点到直线
的距离等于1，则半径R的取值范围是________.
51.函数
取得极小值时，的值为_______.
52．已知椭圆的对称轴是坐标轴，O为坐标原点，F是一个焦点，A是一个顶点.若椭圆的长轴长6，且
，则椭圆的方程是_____________.
53．已知曲线
上点处的切线为，曲线
上点
处的切线，且
，垂足为（1，2）
，则的坐标为_______.
54.椭圆
和圆
是半焦距）无公共点，则椭圆离心率
的取值范围是__________.