数学竞赛单元训练题
不等式
一、选择题
1、已知![]() 、
、![]() 、
、![]()
![]() ,且
,且![]() ,则
,则![]() 的最小值为( )
的最小值为( )
A.![]() B.
B. ![]() C.
C.![]() D.2
D.2
2、已知实数![]() 、
、![]() 、
、![]() 、
、![]() ,满足
,满足![]() ,
,![]() ,则
,则![]() 的最小值与最大值和为 ( )
的最小值与最大值和为 ( )
A.![]() +1 B.
+1 B.![]() +
+![]() +
+![]() D.3
D.3
3、若![]() ,则
,则![]() 的最小值为 ( )
的最小值为 ( )
A.![]() B.
B.![]() C.3 D.
C.3 D.![]()
4、若![]() 、
、![]() 、
、![]() 、
、![]() >0,且
>0,且![]() ,则函数
,则函数![]()
![]() 的最大值为 ( )
的最大值为 ( )
A.20 B.10![]() C.30 D.20
C.30 D.20![]()
5、若不等式![]() ,对一切大于1的自然数
,对一切大于1的自然数![]() 都成立,则整数
都成立,则整数![]() 的最大值为 ( )
的最大值为 ( )
A.44 B.43 C.42 D.41
6、四边形各顶点位于一个边长为1的正方形的各边上,若四边形的边长为![]() 、
、![]() 、
、![]() 、
、![]() ,则有 ( )
,则有 ( )
A.1≤![]() ≤2 B.2≤
≤2 B.2≤![]() ≤4
≤4
C.1≤![]() ≤3 D.3≤
≤3 D.3≤![]() ≤6
≤6
二、填空题
7、设![]() 为自然数,对于任意的实数
为自然数,对于任意的实数![]() 、
、![]() 、
、![]() ,恒有不等式
,恒有不等式![]() ≤
≤![]() 成立,则
成立,则![]() 的最小值为_____________.
的最小值为_____________.
8、长方形的一边长为1,设它被两条互相垂直的直线分成四个小长方形,其中三个的面积不小于1,第四个面积不小于2,则长方形的另一边至少要多长_____________.
9、![]() (其中
(其中![]() 不全为0)的最大值为_____________.
不全为0)的最大值为_____________.
10、已知![]() 、
、![]() 、
、![]()
![]() ,求
,求![]() 的最小值为_____________.
的最小值为_____________.
11、给定正数![]() ,
,![]() 是它的一个排列,则____________使得乘积
是它的一个排列,则____________使得乘积 ![]() 取最大值.
取最大值.
12、四面体P-ABC中,PA、PB、PC互相垂直,设六条棱长的和等于S,则四面体的最大体积为____________.
三、解答题
13、(1)设![]() 、
、![]() 、
、![]()
![]() ,求证:
,求证:![]() ≥1.
≥1.
(2)设![]()
![]() ,且满足
,且满足![]()
求证:![]() ≤
≤![]() .
.
14、已知![]() 、
、![]() 、
、![]() 、
、![]() 是4个不同的实数,使得
是4个不同的实数,使得![]() 且
且![]() ,试求
,试求![]() 的最大值.
的最大值.
15、设![]() 、
、![]() 、
、![]() 、
、![]() 是满足
是满足![]() 的正实数,求证:
的正实数,求证:![]() ≥
≥![]() .
.
16、求最大的实数![]() ,使得当实系数多项式
,使得当实系数多项式![]() 的所有根都是非负实数时,只要
的所有根都是非负实数时,只要![]() ≥min{三根},就有
≥min{三根},就有![]() ≥
≥![]() ,并且问上式中等号何时成立?
,并且问上式中等号何时成立?
数学竞赛单元训练题
解析几何
一、选择题
1、设![]() 和
和![]() ,若
,若![]() ,0
,0![]() 时,恒有
时,恒有![]() ≤
≤![]() ,则实数
,则实数![]() 的取值范围为 ( )
的取值范围为 ( )
A.![]() B.
B.![]() C.
C.![]() D.[ 5,6]
D.[ 5,6]
2、若抛物线![]() 上存在两点
上存在两点![]() 关于直线
关于直线![]() 对称,则
对称,则![]() 的取值范围为( )
的取值范围为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3、设![]() ,
,![]() 为过P(
为过P(![]() ,0)的两条互相垂直的直线,且
,0)的两条互相垂直的直线,且![]() ,
,![]() 与双曲线
与双曲线![]() 各有两个交点,分别为
各有两个交点,分别为![]() 和
和![]() ,则
,则![]() 的斜率
的斜率![]() 的取值范围为 ( )
的取值范围为 ( )
A.1≠![]() <
<![]() B.
B.![]() ≤
≤![]() C.1≠
C.1≠![]() ≤
≤![]() D.以上都不对
D.以上都不对
4、设椭圆C:![]() 的长轴两端点是A、B,若椭圆C存在点Q使
的长轴两端点是A、B,若椭圆C存在点Q使
∠AQB=![]() ,则椭圆C的离心率的取值范围是 ( )
,则椭圆C的离心率的取值范围是 ( )
A.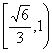 B.
B.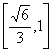 C.
C.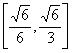 D.
D.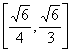
5、设椭圆的中心是坐标原点,长轴在![]() 轴上,离心率
轴上,离心率![]() ,已知点P(0,
,已知点P(0,![]() )到这个椭圆上的点的最远距离是
)到这个椭圆上的点的最远距离是![]() ,则这个椭圆方程为( )
,则这个椭圆方程为( )
A.![]() B.
B.![]() C.
C.![]() D.以上都不对
D.以上都不对
6、在直角坐标系![]() 的平面内,由不等式
的平面内,由不等式![]() ≤
≤![]() ,
,![]() ≤100所确定的图形面积为( )
≤100所确定的图形面积为( )
A.50![]() B.40
B.40![]() C.20
C.20![]() D.30
D.30![]()
二、填空题
7、设![]() 为椭圆
为椭圆![]() 上的
上的![]() 个点,且
个点,且![]() 将圆周角
将圆周角![]() 等分,则
等分,则![]() =____________.
=____________.
8、给定椭圆![]() ,则与这个椭圆有共同焦点的双曲线,使得以它们的交点与顶点的四边形面积最大时,相应的四边形的顶点坐标为____________.
,则与这个椭圆有共同焦点的双曲线,使得以它们的交点与顶点的四边形面积最大时,相应的四边形的顶点坐标为____________.
9、设![]() ,则
,则![]() 的最值是__________.
的最值是__________.
![]()
|
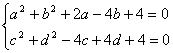 ,则
,则11、如图设N是正数,则图中所示正方形
(包括边界)一共有整点的个数为__________.
12、设抛物线C:![]() 过定点
过定点![]() ,
,![]() ,当
,当![]() (
(![]() )时,不等式
)时,不等式![]() ≥
≥![]() 恒成立时,
恒成立时,![]() 的取值范围是__________.
的取值范围是__________.
三、解答题
13、已知F1,F2是椭圆![]() 的左右焦点,
的左右焦点,![]() 为焦半径,弦AB过右焦点,求三角形F1AB面积的最大值.
为焦半径,弦AB过右焦点,求三角形F1AB面积的最大值.
14、过点(1,0)的直线![]() 与中心在原点,焦点在
与中心在原点,焦点在![]() 轴上,且离心率为
轴上,且离心率为![]() 的椭圆C相交于A、B两点,直线
的椭圆C相交于A、B两点,直线![]() 过线段AB中点,同时椭圆C上存在一点与右焦点关于直线
过线段AB中点,同时椭圆C上存在一点与右焦点关于直线![]() 对称,求直线
对称,求直线![]() 及椭圆C的方程.
及椭圆C的方程.
15、已知抛物线y2=2px (p>0),其焦点F,试问:是否存在过F点的弦AB(A、B均在抛物线上,且A点在第一象限),以及![]() 轴正半轴上一点P ,使得P、A、B三点构成一个以P为直角顶点的直角三角形?证明你的结果,如果结果是肯定的,请求出直线AB的方程.
轴正半轴上一点P ,使得P、A、B三点构成一个以P为直角顶点的直角三角形?证明你的结果,如果结果是肯定的,请求出直线AB的方程.