不等式
一、预备知识：
1、几个著名不等式
平均不等式：
柯西不等式：
排序不等式：
凸函数及琴生不等式：
赫尔德不等式：
切比雪夫不等式：
2、和式的变换
二、著名不等式在竞赛中的运用
例1、已知0≤
≤
≤……≤
＜1，
求证：
·
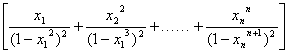＜1
例2、已知
、
、
∈
，且满足
，求证：
≤
例3、设
，
，求证：
≥
例4、设、为正常数，
，，求证：
≥
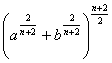
三、利用和式变换解题
例5、设
，而
≥
≥……
≥0，又
≤
（
）
试证：
≤
例6、证明：使对任何满足≤≤……≤的实数， 不等式
≤
都成立的充分必要条件是≥（
），及
=
三、利用递推关系解题
例7、设，，……是正数，
是自然数，求证：
≥
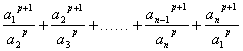例8、设、为正整数，
求证：
≥
四、用其他方法解题
例9、设
为（1，
）→（1，）的函数，且满足对任意
，
＞1及
，
＞0都成立着
≤
·
，试确定所有这样的函数．
例10、试决定下式的最小值
（对一切可能的实值函数0≤
≤1，
）（0≤
≤1，1≤
≤n）．